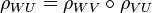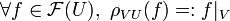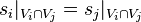Préfaisceau - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, et plus particulièrement dans la théorie des catégories, un préfaisceau sur un espace topologique X est un foncteur contravariant de la catégorie des ouverts de X dans une autre catégorie. On peut donc avoir des préfaisceaux d'ensembles, de groupes, d'anneaux ou de tout autre type de structures mathématiques. Les préfaisceaux préfigurent les faisceaux. En géométrie, aussi bien d'ailleurs en géométrie algébrique qu'en géométrie différentielle, la notion de faisceau est une généralisation des sections d'un fibré vectoriel. Dans ce cadre, X est une variété algébrique ou une variété différentielle.
Les faisceaux ont été introduits dans les années 1940 pour les besoins de la géométrie complexe par Henri Cartan, puis par Jean Leray en topologie. Les faisceaux ont pris par la suite une importance considérable.
Préfaisceaux
Soit X un espace topologique et


- Pour tout ouvert U de X, un objet
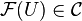
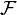
- Pour tout ouvert V inclus dans U, un morphisme
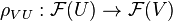
donnés tels que, pour toutes inclusions d'ouverts
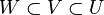
De façon équivalente, on peut définir un préfaisceau
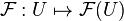
Les faisceaux courants sont à valeurs dans les catégories des groupes, anneaux, espaces vectoriels et algèbres. Il est d'usage d'utiliser les notations suivantes (pour la justification intuitive, voir les exemples qui suivent). Pour tout
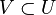
Exemples
- L'exemple fondamental de préfaisceau est celui où les morphismes de restriction sont les restrictions usuelles de fonctions. Notamment sur une variété différentielle X, l'ensemble
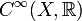
- Dans le plan complexe, une équation différentielle ordinaire, linéaire et à coefficients holomorphes, étant donnée, les espaces de solutions sur des ouverts évitant les points singuliers de l'équation forment un préfaisceau (et même un faisceau) d'espaces vectoriels de dimension égale à l'ordre de l'équation.
- Dans n'importe quelle catégorie, soit X une variété (ou objet) de cette catégorie, alors Hom( * ,X) est un faisceau sur la catégorie, c'est même l'exemple canonique car on plonge toujours une catégorie dans son topos et tout faisceau, F, est représenté dans le topos (ou catégorie des faisceaux) par Hom( * ,F). En particulier, dans les exemples précédents :
- Dans la catégorie des variétés différentielles où les flèches sont les fonctions
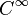
- On prend Y muni de sa topologie séparée et alors le faisceau devient Hom( * ,Y).
- dans la catégorie des ouverts de

- Dans la catégorie des variétés différentielles où les flèches sont les fonctions
On remarquera que si la catégorie admet un objet terminal, pt (pt pour point), alors Hom( * ,pt) est l'objet terminal du topos (donc noté pt) et que si la catégorie admet un objet initial,
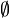
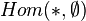
Faisceaux
Pour ce qui concerne les fonctions continues ou les fonctions
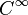
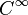
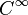
Un préfaisceau


il existe une unique section s de

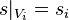
Remarque : comme la famille vide constitue un recouvrement de l' ouvert vide, la condition ci-dessus entraîne que
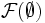
Pour une famille d'ouverts {Ui}I comme dans la définition, on note :
-
-
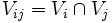
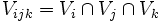
-
Exemples
- Si E est un ensemble, le préfaisceau constant associé, qui par définition envoie tout ouvert sur E, n'est un faisceau que dans le cas où E est un singleton (considérer sa valeur sur l'ouvert vide).
- Les fonctions localement constantes, en revanche, forment bien un faisceau, de même que les fonctions dérivables,
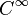
- Soit p un point fixé de X et soit E un ensemble. On peut définir un préfaisceau E_p qui à un ouvert U associe E si U contient p et le singleton sinon. L'application de restriction de U à V est l'identité ou l'unique application de E dans le singleton suivant l'appartenance de p à U et V. On verifie que c'est un faisceau.
Morphismes de préfaisceaux
Les préfaisceaux sur un ensemble X peuvent être considérés comme des objets d'une catégorie. Quelles en sont les flèches ?
Étant donnés deux préfaisceaux

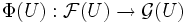

-
-
-
- Φ(V)(s | V) = Φ(U)(s) | V
-
-
Un morphisme de faisceaux est juste un morphisme en tant que préfaisceaux.