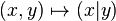Produit scalaire - Définition

Fragments d'histoire

Élément important de calcul en géométrie euclidienne, le produit scalaire apparaît cependant assez tard dans l'histoire des mathématiques. On en trouve trace chez Hamilton en 1843 lorsqu'il crée le corps des quaternions. Peano le définit ensuite associé à un calcul d'aire ou de déterminant. Roberto Marcolongo et Cesare Burali-Forti le définissent seulement à l'aide du cosinus d'un angle et lui donnent le nom de produit intérieur ou produit scalaire. C'est sous cette forme qu'il apparaît par la suite. Sa qualité de forme bilinéaire symétrique sera ensuite exploitée en algèbre linéaire et, de propriété, deviendra définition.

La notation du produit scalaire à l'aide d'un point ou d'une croix provient de Josiah Willard Gibbs, dans les années 1880.

Pourtant, selon le site Earliest known uses of some of the mathematical words, l'expression produit scalaire apparait pour la première fois dans une publication scientifique dans un livre de William Kingdon Clifford daté de 1878. Cette paternité est néanmoins remise en cause par M. J Crowe pour qui Clifford est une transition entre l'algèbre des quaternions décrite par Hamilton et la formalisation des espaces vectoriels.

Propriétés algébriques

Pour une raison de simplicité, d'autres notations sont utilisées. Les vecteurs ne sont plus notés comme des bipoints, comme par exemple mais simplement avec une lettre : . Le produit scalaire est alors toujours noté par un point : . Il arrive aussi que les vecteurs soient notés sans flèches, pour éviter la confusion entre le produit d'un scalaire par un vecteur et le produit scalaire entre deux vecteurs, le produit scalaire est alors noté (u, v) ou encore . Une convention, pas toujours suivie consiste à choisir des lettres grecques pour les scalaires, permettant ainsi d'éviter des confusions. Dans la suite de l'article, la convention suivie est celle du vecteur surmonté d'une flèche et du produit scalaire noté par un point.

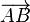
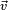
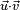
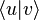
Le terme de produit scalaire suggère l'existence d'une opération qui, à deux vecteurs, associe un scalaire. Dans un espace vectoriel, les scalaires sont les coefficients par lesquels on a le droit de multiplier les vecteurs. Dans une approche élémentaire, ces scalaires sont des réels. Le fait d'appeler cette opération un produit suggère l'existence de propriétés que l'on attend généralement d'un produit (commutativité, distributivité par rapport à l'addition...).

Symétrie

La symétrie est une propriété qui s'applique aux fonctions de deux variables prises dans un même ensemble. Soit un ensemble E et une fonction f définie dans E×E. Elle est dite symétrique si et seulement si :

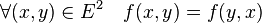
Le cadre de cette définition est celui du produit scalaire, qui à deux vecteurs associe un nombre.

Comme la longueur du segment [B, C] est celle du segment [C, B], le théorème d'Al-Kashi établit la symétrie du produit scalaire :

Symétrie du produit scalaire

Le produit scalaire défini sur un espace vectoriel E est symétrique, c'est-à-dire que la proposition suivante est toujours vérifiée :

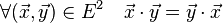
Bilinéarité

Le produit scalaire dans un espace vectoriel E est compatible à droite avec l'addition. Cette propriété signifie que le produit scalaire d'un vecteur par une somme de deux vecteurs est égal à la somme des deux produits scalaires :

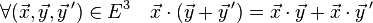
La figure de gauche illustre cette compatibilité. Elle est la conséquence du fait que la translation laisse invariante l'aire d'une surface. Une application de cette nature, laissant invariant les angles, les longueurs et par voie de conséquence les surfaces est appelée isométrie. Le rectangle vert a pour surface le produit scalaire de avec , le rectangle bleu a pour surface le produit scalaire de avec . La somme des deux surfaces est bien égale à la surface du rectangle orange qui est le produit scalaire de avec . En effet, la translation laisse invariante la surface. L'égalité recherchée est bien vérifiée.

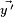
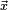
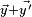
La symétrie du produit scalaire ainsi que la compatibilité à droite démontre la compatibilité à gauche de l'addition :

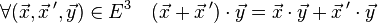
Il est de même possible de parler de compatibilité à droite pour le produit par un scalaire. Cette propriété prend la forme suivante :

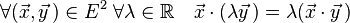
Le point désigne ici à la fois la multiplication par un scalaire et le produit scalaire. L'usage des flèches ainsi que des lettres grecques pour désigner des nombres permet d'éviter l'ambigüité.

Cette compatibilité est une conséquence du théorème de Thalès. La figure de droite illustre cette propriété. Le rectangle violet possède une hauteur égale à celle du triangle vert, et sa base est égale à OD. Les deux triangles OAB et OCD sont semblables il est donc possible d' appliquer le théorème de Thalès, il démontre que comme OC = λ⋅OA, alors OD = λ⋅OB. Sa surface est donc bien multipliée par λ.

Comme précédemment, la symétrie possède pour conséquence la compatibilité à gauche :

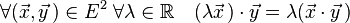
Ainsi, l'application, pour un qui au vecteur associe le nombre vérifie la propriété suivante :

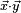
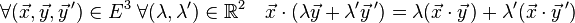
On dit alors que l'application produit scalaire est linéaire à droite, elle est de même linéaire à gauche. Une telle application est dite bilinéaire. L'application a pour valeurs des nombres, on parle alors de forme.

Bilinéarité : le produit scalaire est une forme bilinéaire.

Caractère défini positif

Le produit scalaire d'un vecteur avec lui-même est égal à l'aire d'un carré de côté la longueur d'un de ses représentants. En conséquence, le produit scalaire d'un vecteur avec lui-même est toujours positif. Cette valeur est nulle si et seulement si le vecteur est nul car seul le vecteur nul possède un représentant de longueur nulle. On en déduit la définition et la proposition suivantes :

Une forme à deux variables est dite définie positive si et seulement si pour tout vecteur non nul x, l'image de (x,x) est strictement positive.

Le produit scalaire est une forme définie positive.

Bilan : produit scalaire réel

Un produit scalaire est une forme bilinéaire symétrique définie positive sur un espace vectoriel sur les nombres réels.

Les propriétés algébriques vues dans le cas de la dimension 2 ou 3 sont suffisantes pour définir un produit scalaire dans un espace vectoriel réel quelconque.

Soit un espace vectoriel réel.

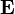
On dit qu'une application φ :

est un produit scalaire si elle est :

• bilinéaire : φ est linéaire relativement à chaque argument (l'autre étant fixé).
• symétrique :
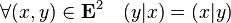
• positive :
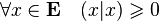
• définie :

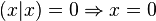
Il est naturel de se poser la question réciproque : Est-il possible de définir une géométrie à l'aide d'un espace vectoriel et d'un produit scalaire ? La longueur est alors donnée par la norme, et l'angle θ entre deux vecteurs et par la formule :

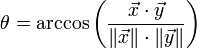
Une telle géométrie vérifie les inégalités triangulaires et de Cauchy-Schwarz, le théorème de Thalès, de Pythagore, ses isométries sont les rotations et les symétries.

Espace euclidien

Un espace euclidien est un espace vectoriel sur , de dimension finie et muni d'un produit scalaire.

Un tel espace possède de nombreuses propriétés à la fois algébriques et géométriques. Le produit scalaire met en évidence des applications linéaires particulières aux propriétés multiples. Elles permettent, entre autres, de définir de nombreuses structures additionnelles, souvent elles aussi euclidiennes. Elle offre un cadre géométrique qui permet de généraliser bon nombre de résultats vrais sur les nombres réels. Il devient ainsi possible d'appliquer des résultats de l'analyse réelle à la géométrie différentielle.