Résistance thermique de conduction - Définition

Introduction

La résistance thermique de conduction, aussi appelée résistance thermique conductive, d’un élément exprime sa résistance au passage d’un flux de conduction thermique. Cette résistance s’applique aux solides ainsi qu’aux fluides (liquide ou gaz) immobiles. Dans le système international d'unités, elle est donnée en kelvin par watt (K/W) ou °C/W. Cette notion n’est valable qu’en régime stationnaire, le régime transitoire faisant appel à la notion plus complexe de quadripôle thermique. Son inverse est la conductance thermique.

Expression

La résistance thermique de conduction s'exprime en fonction du flux de chaleur entre deux surfaces isothermes et les températures de ces deux surfaces isothermes :

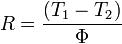
• T₁ et T₂ sont les températures des deux isothermes exprimées en kelvin ;
• Φ est le flux de chaleur entre les deux isothermes, en watt ;
• R la résistance thermique de conduction en K/W.

En fonction de la résistance thermique de conduction, le flux de chaleur s'exprime de la sorte :

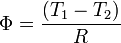
Ainsi, pour une même différence de température plus la résistance thermique est forte moins la quantité de chaleur traversant le corps est forte. Un isolant thermique est donc un corps qui possède une résistance thermique de conduction importante.

La résistance thermique est définie par rapport à des surfaces isothermes. La géométrie de ces surfaces dépend de la géométrie de l'objet dans lequel la conduction thermique se produit. Différents cas particuliers usuels peuvent être décrits.

Surface plane

Les isothermes sont des surfaces planes et parallèles, c'est par exemple le cas d'un mur de maison. La résistance thermique de conduction R d’un élément d’épaisseur e (en m), de surface S (en m²), et de conductivité thermique K (en W·m^-1·K^-1) vaut :

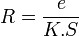
La résistance thermique s'exprime en K·W^-1.

Cette formule néglige les effets de bord en supposant que les dimensions (longueur, largeur) de l’élément sont très grandes devant son épaisseur ( et ). On suppose aussi que les matériaux constituant l’élément sont isotropes, c’est-à-dire que leur comportement thermique est le même quelle que soit la direction. L’élément peut être constitué de différents matériaux isotropes (ou considéré comme tel), par exemple un mur en brique recouvert d’un enduit à l’extérieur et d’un isolant à l’intérieur.

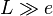
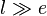
Surface cylindrique

Les isothermes sont des cylindres concentriques, c'est par exemple le cas d’un tuyau, d’une canalisation, etc. La résistance thermique de conduction R d’un élément cylindrique de longueur l, de rayon interne R₂ et externe R₁ vaut :

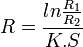
Avec S = 2πl

Dans le bâtiment

Dans le domaine du bâtiment on peut trouver la définition de la résistance thermique d’un matériau (par exemple un isolant) intrinsèque, c’est-à-dire en ne tenant pas compte de la surface exposée :

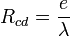
où :

• e est l'épaisseur en m
• λ est la conductivité thermique en W K^-1 m^-1
• R_cd (ou simplement R) est la résistance thermique en m².K/W

La résistance thermique des matériaux est parfois utilisée dans les règlementations thermiques, telles que la RT 2005 en France. Cependant cette grandeur est petit à petit abandonnée au profit du coefficient de transfert thermique U, qui prend aussi en compte la mise en œuvre du produit.

En électronique

Les éléments semi-conducteurs de puissance sont généralement montés sur des dissipateur thermiques (ou refroidisseurs) destinés à favoriser l’évacuation de l’énergie produite au niveau des jonctions anode-cathode pour les diodes, les thyristors, les triacs, et les GTO ou collecteur-émetteur pour les transistors bipolaires et les IGBT, ou drain-source pour les MOSFET. Dans ce cas, la résistance thermique entre la jonction et l'air ambiant est une somme de trois résistances thermiques :

Résistance thermique jonction-boîtier

Elle est donnée dans les feuilles de caractéristiques du constructeur. Voici quelques ordres de grandeur de résistances thermiques selon les types de boîtiers courants :

• petits boîtiers cylindriques, plastiques ou métalliques (TO-39 / TO-5, TO-92, TO-18) : entre 20 et 175 K/W ;
• boîtiers intermédiaires plats, plastiques (TO-220, TO-126/SOT-32) : entre 0,6 et 6 K/W ;
• boîtiers moyens de composants de puissance, plastiques ou métalliques (ISOTOP, TO-247, TOP-3, TO-3) : de 0,2 à 2 K/W ;
• boîtiers de composants modulaires de puissance : de 0,01 à 0,5 K/W.

Le transfert thermique entre la jonction et le boîtier se fait essentiellement par conduction.

Résistance thermique boîtier-dissipateur thermique

Elle dépend de la surface de contact entre l'élément et le dissipateur et de la présence ou non d'un isolant électrique. Le transfert thermique entre le boîtier et le dissipateur se fait essentiellement par conduction. Par exemple pour un boîtier TO-3 : sans isolant, à sec : 0,25 K/W ; sans isolant, avec graisse de silicone : 0,15 K/W ; avec isolant mica 50 µm et graisse de silicone : 0,35 K/W.

Résistance thermique dissipateur thermique-ambiance