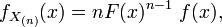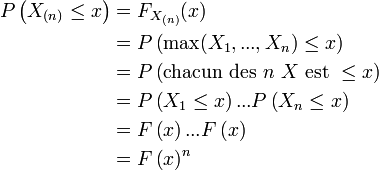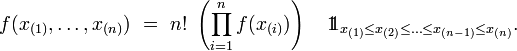Statistique d'ordre - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En statistiques, la statistique d'ordre de rang k d'un échantillon statistique est égal à la k-ieme plus petite valeur. Associée aux statistiques de rang, la statistique d'ordre fait partie des outils fondamentaux de la statistique non paramétrique et de l'inférence statistique.
Deux cas importants de la statistique d'ordre sont les statistiques du minimum et du maximum, et dans une moindre mesure la médiane de l'échantillon ainsi que les différents quantiles.
Quand on emploie la probabilité pour analyser les statistiques d'ordre d'un échantillon aléatoire issu d'une distribution continue, la fonction de distribution cumulative est employée pour ramener l'analyse au cas de la statistique d'ordre sur une distribution uniforme
Notation et exemples
Soit une expérience conduisant à l'observation d'un échantillon de 4 nombres, prenant les valeurs suivantes :
- 6, 9, 3, 8,
que l'on note selon la convention :
où le i en indice sert à identifier l'observation (par son ordre temporel, le numéro du dispositif correspondant, etc.), et n'est pas a priori corrélée avec la valeur de l'observation.
On note la statistique d'ordre :
où l'indice (i) dénote la i-ième statistique d'ordre de l'échantillon suivant la relation d'ordre habituelle sur les entiers naturels.
Par convention, la première statistique d'ordre, notée X(1), est toujours le minimum de l'échantillon, c'est-à-dire :
Suivant la convention habituelle, les lettres capitales renvoient à des variables aléatoires, et les lettres en bas de casse aux valeurs observées (réalisations) de ces variables.
De même, pour un échantillon de taille n, la statistique d'ordre n (autrement dit, le maximum) est
Les statistiques d'ordre sont les lieux des discontinuités de la fonction de répartition empirique de l'échantillon.
Analyse probabiliste
Densité d'une statistique d'ordre
Étant donné une échantillon
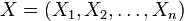
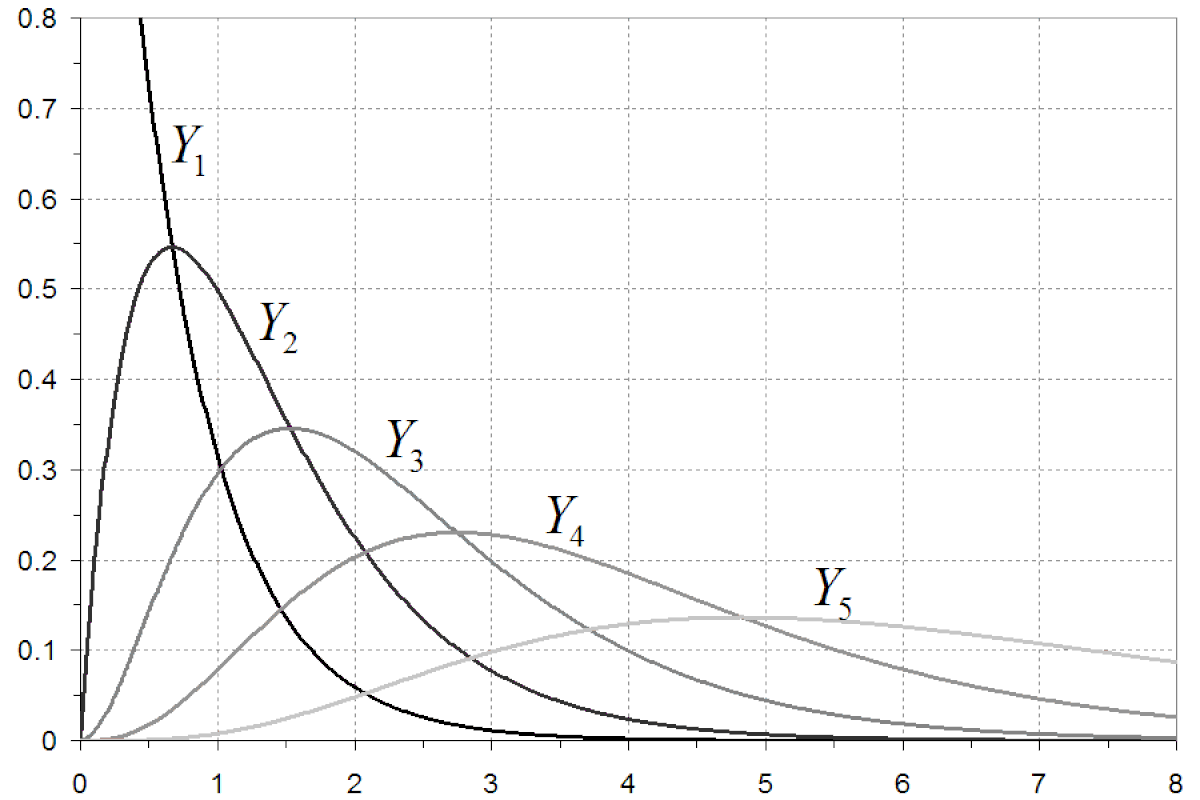
Théorème — Si on suppose l'échantillon X indépendant et identiquement distribué selon une loi de densité f et de fonction de répartition F, alors la densité de la k-ème statistique d'ordre est
Calcul via la fonction de répartition
La fonction de répartition de la k-ème statistique d'ordre est
Autrement dit, le nombre d'éléments de l'échantillon inférieurs à x suit une loi binomiale de paramètres n et F(x), puisqu'il s'agit là de n expériences indépendantes, possédant deux issues : « être inférieur à x » et « être supérieur à x », la première des deux issues ayant pour probabilité F(x), et la deuxième issue ayant pour probabilité 1-F(x). En dérivant, on trouve une somme télescopique qui donne la densité :
car
Finalement :
Calcul direct
Lors d'une série de n expériences aléatoires indépendantes et identiques ayant chacune trois issues possibles, disons a, b, et c, de probabilités respectives pa, pb, pc, la loi jointe des nombres d'issues Na (resp. Nb, Nc ) de type a (resp. b, c) est une loi multinomiale de paramètres n et p=(pa, pb, pc ), décrite par :
Ainsi, la densité de X(k) est obtenue en reconnaissant une série de n expériences aléatoires indépendantes et identiques ayant chacune trois issues possibles, Xi ≤ x, x
En particulier
formule qu'on peut trouver directement, en dérivant le résultat du calcul ci-dessous :
Pour la loi uniforme continue, la densité de la k-ème statistique d'ordre est celle d'une Loi bêta, de paramètres k et n+1-k.
Densité jointe de toutes les statistiques d'ordre
Théorème — Si on suppose l'échantillon X indépendant et identiquement distribué selon une loi de densité f, alors la densité jointe des n statistiques d'ordre est
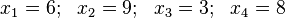
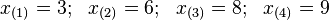
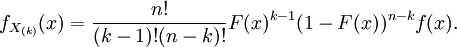
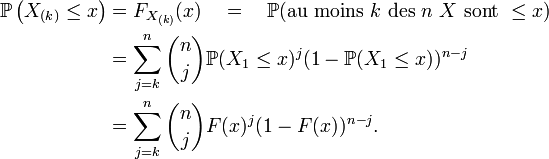
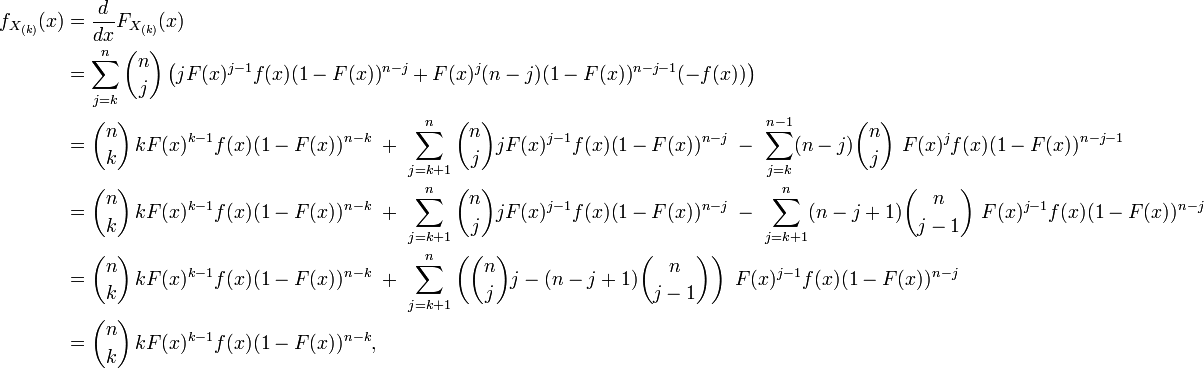
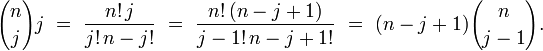
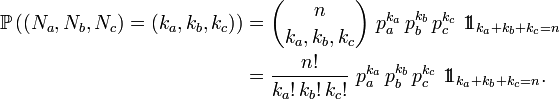
![\begin{align} f_{X_{(k)}}(x)\ dx& {} = \mathbb{P}\left(X_{(k)}\in [x,\, x+dx]\right) \\& {}\mathbb{P}\left(\text{ parmi les }n\ X_i,\text{exactement}\ k-1\ \text{sont}\ \leq x,\text{exactement un des }X_i\in[x,\, x+dx],\text{et les autres sont}\ \ge x+dx\right) \\ &= \frac{n!}{k-1!\,1!\,n-k!}\ F(x)^{k-1}\,f(x)\, dx\,(1-F(x)-f(x)dx)^{n-k} \\ &=\frac{n!}{k-1!\,n-k!}\ F(x)^{k-1}\,(1-F(x))^{n-k}\,f(x)\, dx. \end{align}](https://static.techno-science.net/illustration/Definitions/autres/3/399a8223e2ed8640584cdbc658c92fab_cda734f953578f85d4bb5a2434e1143d.png)