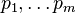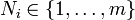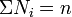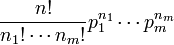Loi multinomiale - Définition

Introduction

Multinomiale
Paramètres	n > 0 nombre d'épreuves (entier) probabilités des événements (Σpi = 1)
Support
Densité de probabilité (fonction de masse)
Espérance	E{Xi} = npi
Variance	Var(Xi) = npi(1 − pi) Cov(Xi,Xj) = − npipj ( )
Fonction génératrice des moments
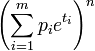
modifier

La loi binomiale concerne le nombre de succès dans n épreuves de Bernoulli indépendantes donnant chacune un résultat binaire, comme dans le jeu de pile ou face. La loi multinomiale est une généralisation de celle-ci, applicable par exemple à n jets d'un dé à six faces. Contrairement à ces exemples simples, les différentes possibilités ne sont généralement pas équiprobables.

Autre présentation de la loi binomiale

La fonction de probabilité de la variable aléatoire binomiale qui s'écrit

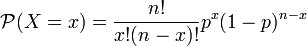
peut se réécrire de manière symétrique en faisant intervenir deux variables dont la somme est égale à n :

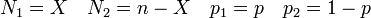
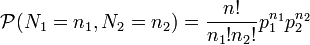
Approximation

Lorsque la variable aléatoire devient assez grande, le théorème de la limite centrale montre qu'elle est raisonnablement approchée par une variable normale à laquelle correspond la variable centrée réduite .

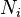
Si ces variables étaient indépendantes, suivrait une loi du à degrés de liberté.

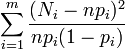
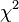
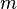
Du fait de la contrainte linéaire qui s'applique, la variable suit une loi du à degrés de liberté.

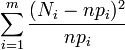
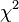
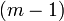
Cette dernière remarque est à la base du test du χ².

Généralisation

Dans le cas multinomial à résultats possibles au lieu de 2, les variables deviennent , et correspondent aux probabilités , avec les contraintes

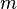
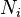
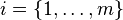
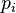
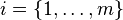
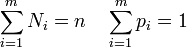
La fonction de probabilité s'écrit alors, sous la condition portant sur la somme des variables :

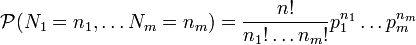
Chacune des variables reste une variable binomiale dont la moyenne et la variance sont

tandis que les covariances s'écrivent