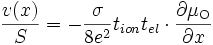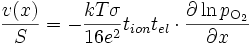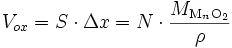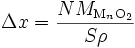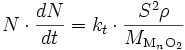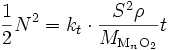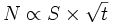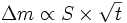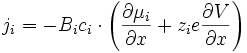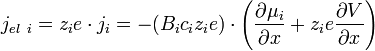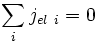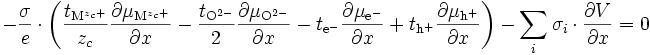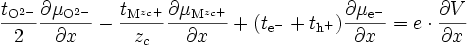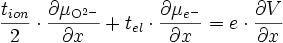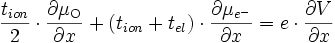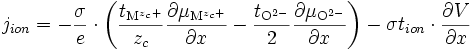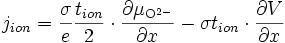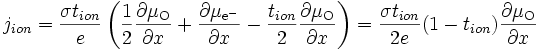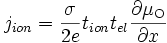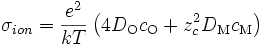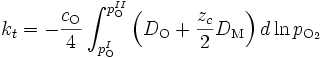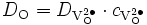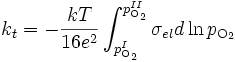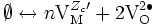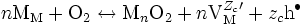Théorie de la cinétique d'oxydation de Wagner - Définition

Vitesse de croissance

D'après () et (), on a :

où v(x) est le nombre de cellules de M_nO₂ crées en une seconde à la profondeur x par rapport à la surface (toutes les grandeurs sont en effet locales).

En remplaçant l'activité de l'oxygène par la pression partielle de dioxygène , on obtient

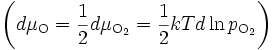
En intégrant cette équation sur l'épaisseur Δx de la couche, on obtient :

(19)

où

• N est le nombre de moles d'oxyde ;
• p^I_O2 et p^II_O2 sont les pressions partielles d'oxygène aux interfaces oxyde/gaz et oxyde/métal ;
• k_t est le coefficient d'oxydation parabolique.

Si l'on considère que la densité de l'oxyde est uniforme, l'épaisseur Δx de la couche est proportionnelle à la quantité d'oxyde N (Δx ∝ N) : le volume d'oxyde V_ox s'écrit

où ρ est masse volumique de l'oxyde et M_MnO2 est sa masse molaire. On a donc

et donc

donc en intégrant

puisqu'en début d'oxydation, la quantité d'oxyde est nulle (N = 0 à t = 0), soit

Comme la prise de masse est due à l'incorporation d'atomes d'oxygène, on a

Δm = N⋅2⋅M_O

où 2 est le nombre d'atomes d'oxygène par maille de M_nO₂, et M_O est la masse molaire de l'oxygène (16 g·mol⁻¹), donc

Ce sont donc bien des lois paraboliques.

Courant ionique

Les espèces chargées migrent sous l'effet du gradient de potentiel chimique et électrique, donc pour une espèce i () () :

Ce flux crée un courant électrique dont la densité vaut () () () :

soit d'après ():

(E15).

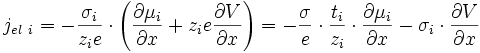
puisque σ_i = t_i·σ.

Le circuit est ouvert : il n'y a pas de circulation de charges à l'extérieur de l'oxyde, on a donc :

soit

Comme on a

∑	σi = σ
i

et avec (), on obtient :

et d'après () :

(E16)

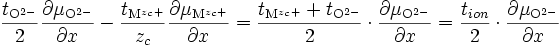
si l'on note le nombre de transport ionique t_ion = t_Mzc+ + t_O2- et le nombre de transport électrique t_el = t_e- + t_h+. On obtient :

et d'après ()

comme t_ion + t_el = 1, on obtient

(E17)

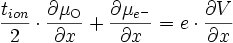
La quantité qui nous intéresse est le courant ionique, qui s'écrit d'après () :

soit d'après ()

en utilisant l'équilibre thermodynamique de l'oxygène () et en remplaçant par l'expression trouvée en (), on a :

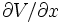
soit

(E18)

Cas particuliers

Défauts prédominants et diffusion

Dans le cas général, on a deux défauts dominants : un défaut ionique (dans le sous-réseau d'oxygène ou de métal) et un défaut électronique (électron libre ou trou délectron).

En raison de la neutralité électrique, les défauts doivent avoir une charge de signe opposé, on a donc quatre possibilités :

1. lacunes métalliques V_M^zc ' et des trous d'électron h^•, l'oxyde est alors dit « en déficit métallique » ;
2. ions métalliques interstitiels M_i^{zc •} et électrons libres e', l'oxyde est alors dit « en excès métallique » ;
3. lacunes d'oxygène V_O^{2 •} et électrons libres e' ; l'oxyde est alors dit « en déficit d'oxygène » ;
4. ions oxygène interstitiels O_i² ' et trous d'électron h^• ; l'oxyde est alors dit « en excès d'oxygène ».

Les électrons et trous d'électron étant beaucoup plus rapide que les ions, l'oxyde se comporte comme un semi-conducteur de type P dans les cas 1 et 4, et de type N dans les cas 2 et 3.

Dans certains cas, lorsque que l'oxyde est proche de la stœchiométrie, les deux défauts prédominants peuvent être ioniques et former des défauts de Frenkel V_M^zc ' + M_i^{2 •} ou V_O^{2 •} + O_i² ', ou des défauts de Schottky V_M^zc ' + V_O^{2 •}.

Du fait de la faible concentration en charges électroniques, le conducteur est de type ionique ; on parle « d'électrolyte solide ».

Dans une couche d'oxyde obtenue par réaction avec l'atmosphère, le type de défaut dominant peut varier en fonction de la profondeur puisque la pression partielle de dioxygène varie.

Les considérations ci-dessus ne sont valables que pour de faibles concentrations de défaut (jusqu'à environ 10⁻⁴ par maille, soit un défaut pour 10 000 mailles). Au delà, les défauts interagissent et ne peuvent plus être considérés comme indépendants. Pour des concentrations élevées (fraction supérieure à 10⁻²), les défaut forment des « associations (ou amas) de défauts » (defect clusters). Un ion interstitiel de charge positive (ion métallique ou impureté) ayant une charge relative opposée à la lacune métallique, la présence d'interstitiels a tendance à stabiliser les lacunes par attraction coulombienne (électrostatique) ; lorsque l'on a a interstitiels entourés de b lacunes, on parle de défaut (b : a). Un exemple simple est l'amas de défauts (4:1) dans le wüstite Fe_1-zO (structure NaCl).

Oxyde ayant une conductivité électronique prédominante

On a t_el ≈ 1 et t_ion << 1, soit

σ⋅t_ion⋅t_el ≃ σ⋅t_ion = σ_ion

avec

.

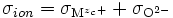
D'après (), on a donc

k_t dépend donc des coefficients d'autodiffusion des anions et des cations dans l'oxyde (qui eux-mêmes dépendent de la pression de dioxygène dans l'oxyde) :

Or, les coefficients de diffusion D_M et D_O s'expriment en fonction des coefficients d'autodiffusion des défauts et de leur concentration, par exemple dans le cas d'un oxyde déficitaire en oxygène,

la concentration en défaut peut elle-même se déduire de la pression partielle de dioxygène. Ainsi, il est possible d'exprimer k_t en fonction des paramètres fondamentaux du matériau et de l'environnement.

Oxyde ayant une conductivité ionique prédominante

Si l'oxyde a une conductivité ionique prédominante, alors la diffusion est limitée par le transport des électrons et des trous d'électron. On a t_ion ≈ 1 et t_el << 1, soit

σ⋅t_ion⋅t_el ≃ σ_el

et donc

Les équilibres de défauts permettent de relier la concentration en électrons à celle des trous d'électrons en fonction de la pression partielle de dioxygène. Si par exemple on suppose que le défaut prédominant est le défaut de Schottky chargés et que les trous d'électron sont prédominants sur les électrons, on a

avec donc la constante d'équilibre

.

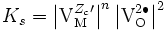
Par ailleurs, on a

avec la constante d'équilibre

.

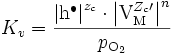
On peut ainsi exprimer le coefficient parabolique d'oxydation en fonction de K_s, K_v et de p_O2 .