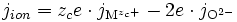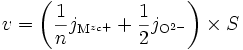Théorie de la cinétique d'oxydation de Wagner - Définition

Introduction

La théorie de la cinétique d'oxydation de Wagner est une théorie physique destinée à modéliser la vitesse de croissance d'une couche d'oxyde sur un métal lorsque celle-ci est compacte et adhérente, dans le cadre de la corrosion sèche. Elle fut proposée par Carl Wagner en 1933.

Cette théorie prédit une loi parabolique : la masse oxydée, ou la prise de masse Δm, est proportionnelle à la surface réactive S et à la racine carrée du temps t :

.

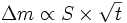
Ce comportement en racine carrée du temps est également constaté expérimentalement. Intuitivement, on peut concevoir que la croissance est de moins en moins rapide car les espèces chimiques doivent traverser une couche d'oxyde de plus en plus épaisse.

Le calcul fait par Wagner prend en compte la diffusion sous l'effet de l'agitation thermique, les charges des espèces et notamment la force électrostatique qui s'y exerce, ainsi que les équations thermochimiques qui résultent du quasi-équilibre chimique à chaque point de l'oxyde.

Cependant, cette loi fait des hypothèses trop restrictives, et la cinétique calculée à partir de cette théorie ne correspond pas aux résultats expérimentaux (la forme de la courbe correspond, mais pas l'échelle). Elle reste malgré tout la loi la plus complète et sert de base à d'autres extrapolations prenant en compte, par exemple, l'effet des joints de grain.

Introduction

Pour traiter le problème de la cinétique d'oxydation à haute température, Wagner a fait les hypothèses suivantes quant à la migration des espèces dans l'oxyde :

• la migration fait intervenir, outre le déplacement par sauts aléatoires (diffusion), l'effet du gradient de potentiel chimique ainsi que l'effet du champ électrique local créé par la répartition des charges ;
• l'oxyde a une composition proche de la stœchiométrie ;
• à tout instant, l'oxyde est localement à l'équilibre chimique ;
• le circuit est ouvert, c'est-à-dire que le courant électrique global est nul et donc que les flux d'espèces chargées sont couplés.

La formation d'oxyde se fait par diffusion d'ions, le but est donc de calculer le flux ionique en fonction des paramètres fondamentaux de l'oxyde (coefficient de diffusion, conductivités, pression partielle d'oxygène).

Convention de notation et stratégie

On considère que l'oxyde a pour formule :

M_nO₂

où « M » est un métal. On peut dans une première approche considérer que c'est un cristal ionique, les ions étant alors :

(parfois noté M^{zc +} ) et O^2-.

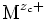
La neutralité électrique du cristal impose qu'il y ait autant de charges positives que de charges négatives, soit

n × z_c = 2 × 2 = 4 (E1)

Il s'agit là de la neutralité électrique « constitutive », « stœchiométrique », de l'oxyde. Lors de l'oxydation, il se forme d'autres charges (comme les électrons libres et les trous d'électron), il y a donc une autre équation de la neutralité électrique qui prend en compte les concentrations des différentes espèces.

On considère qu'une « cellule élémentaire » M_nO₂ se forme par la rencontre de n ions métalliques M^{zc +} et de deux ions oxygène O^2- selon la réaction :

n M^{zc +} + 2 O^2- → M_nO₂.

Le but du présent article est donc de présenter un calcul du flux d'ions (nombre d'ions traversant une surface unité perpendiculaire au flux, c'est-à-dire parallèle à la surface libre de l'échantillon, durant un temps unité) :

étant le flux de cations métalliques vers l'extérieur, étant le flux d'anions oxygène vers l'intérieur.

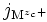
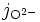
Un flux de particules i chargées crée un courant électrique. Si chaque particule porte z_i charges élémentaires e, alors la densité de courant électrique j_{el i} est reliée au flux de particules j_i par la formule :

(E2)

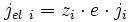
Dans le cas des ions dans l'oxyde, le flux de cations vers l'extérieur et le flux d'anions vers l'intérieur crée un courant électrique nommé « courant ionique », noté j_ion, et valant :

Si la réaction de formation est très rapide devant la migration des espèces, alors pour une surface S, la vitesse v de formation de l'oxyde (en mole par seconde) est :

ce qui, d'après l'électroneutralité () devient

(E3)

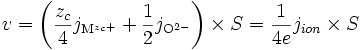
Nous allons donc chercher à déterminer le courant ionique afin de déterminer la vitesse de croissance de l'oxyde.