Variété (géométrie) - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Introduction - Applications des variétés - Histoire - Définition des variétés - Un exemple détaillé : le cercle - Approfondissements - Construction de variétés

Applications des variétés

Les applications des variétés en mathématiques sont nombreuses. Contentons-nous de quelques exemples. Pour commencer, l'analyse réelle classique et l'analyse fonctionnelle ont vu leur terrain d'investigation s'étendre logiquement des espaces vectoriels topologiques aux variétés. De même, les processus stochastiques à l'exemple du mouvement brownien s'étendent des espaces réels de dimension finie aux variétés. Aussi les variétés apparaissent-elles de manière épisodique en statistiques. Plus encore, des ensembles intéressants ont à la fois une structure algébrique et une structure de variété compatibles. Ainsi l'ensemble des rotations dans un espace à 3 dimensions forme une 3-variété et un groupe. La théorie des groupes de Lie étudie ces variétés à propriétés algébriques. La théorie des espaces homogènes étudie leurs actions transitives.

L'espace des configurations d'un système physique

En physique, l'étude des systèmes mécaniques fait entrer en ligne de compte l'ensemble des positions que le système est a priori susceptible d'adopter, appelé espace des configurations. Celui-ci possède souvent une structure de variété ; cependant, il peut ne pas avoir la structure plus rigide de variété différentielle : des singularités peuvent apparaître. La dimension de cette variété s'interprète comme le nombre de paramètres physiques indépendants qui permettent de décrire l'état du système.

Ainsi dans le cas du pendule double dans le plan, l'état du système est complètement décrit par la donnée de deux angles. On pourrait donc être tenté de dire que l'espace des configurations est $[0, 2 \pi] \times [0, 2\pi]$ . Mais en réalité, l'état décrit par le couple d'angles $(0,0)$ est le même que celui décrit par $(2π,2π)$ . Donc il s'agit d'identifier les côtés opposés du carré $[0, 2 \pi] \times [0, 2\pi]$ deux à deux. On obtient ainsi un tore. 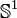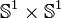De manière équivalente, un angle est paramétré de manière bijective par un point du cercle $\mathbb S^1$ , donc un couple d'angles est paramétré de manière bijective par un point de l'espace $\mathbb S^1 \times \mathbb S^1$ , qui définit aussi le tore. Le premier angle permet de désigner un point sur le cercle rouge, le second un point sur le cercle rose. Le point du tore désigné par les deux angles s'obtient à l'intersection de deux cercles de coordonnées (en gris).

Le pendule double et son espace de configuration : le tore
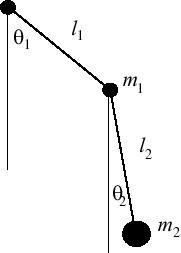La position du pendule double est décrite par deux paramètres angulaires.	La position d'un point sur le tore également.

Les lois de la physique s'interprètent alors comme des équations différentielles écrites sur la variété, et peuvent être traitées dans le cadre de la mécanique lagrangienne. Une reformulation, qui se présente comme un changement de coordonnées locales, débouche sur la mécanique hamiltonienne. Celle-ci utilise comme soubassement mathématique les variétés symplectiques, modélisant l'espace des phases.

L'espace des phases ne se résume pas à l'espace des configurations. La raison en est que la dynamique hamiltonienne fait intervenir des dérivées secondes. De même que dans l'étude des équations différentielles ordinaires d'ordre 2, on ajoute la vitesse à la position pour obtenir des équations ordinaires d'ordre 1. L'opération cependant est plus délicate ici et nécessite une bonne maitrise des structures impliquées : elle fait appel à la théorie des fibrés vectoriels.

Variété (géométrie) - Définition

Applications des variétés

L'espace des configurations d'un système physique

Variétés et physique théorique