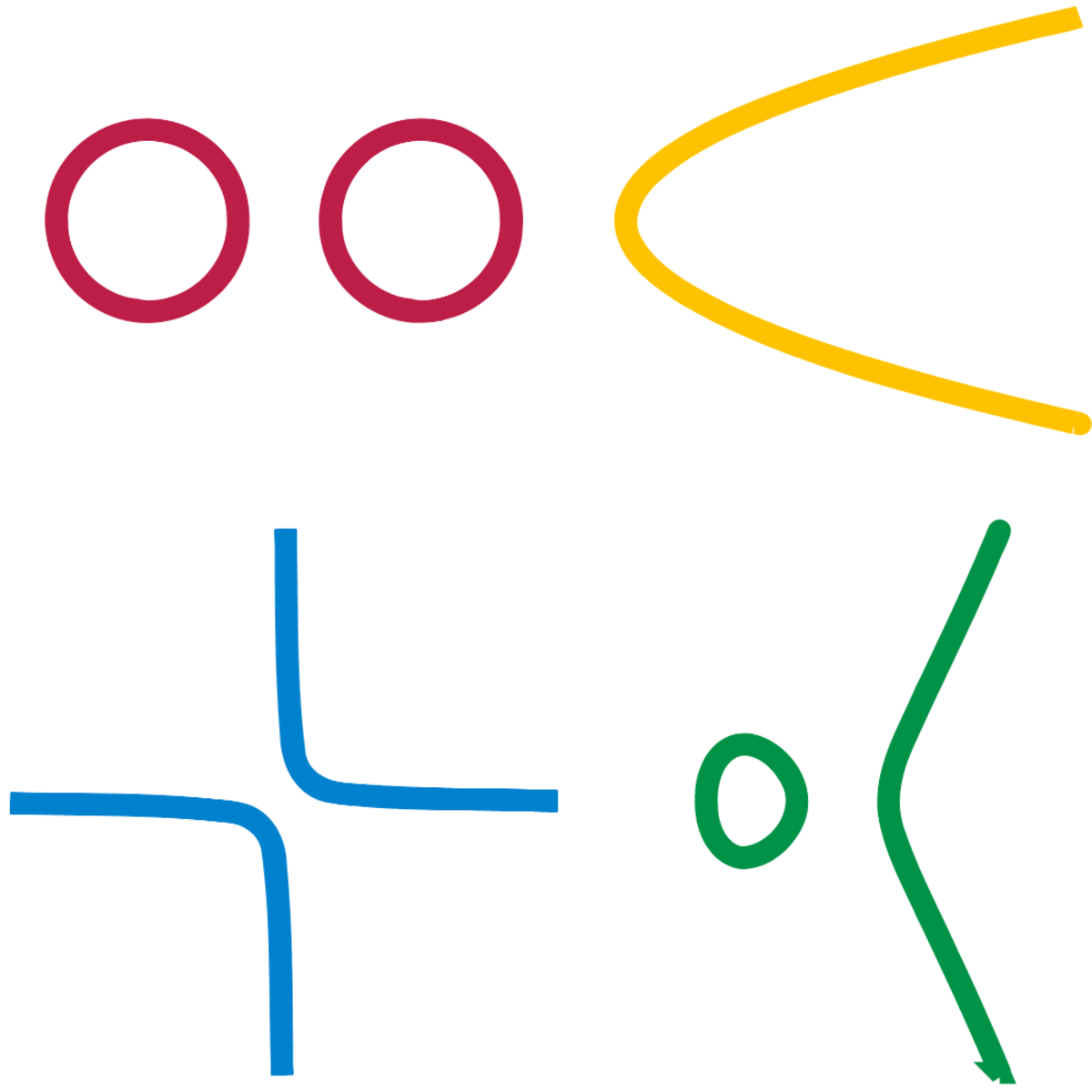Variété (géométrie) - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, une variété est un espace topologique abstrait, construit par recollement d'autres espaces simples. Comme les enfants s'amusent à construire avec du papier des tétraèdres, des cubes et autres polyèdres en dessinant la figure d'un patron sur une feuille blanche, en découpant convenablement les bords, en pliant et en recollant, les mathématiciens obtiennent un cercle en repliant un segment sur lui-même, un cylindre ou un cône en repliant une bande plane sur elle-même. Un autre exemple classique est le ruban de Möbius illustré ci-contre (en toute rigueur, c'est un exemple de ). Il est également possible de rajouter des anses à une sphère.
Parmi les variétés les plus simples figurent les courbes et surfaces du plan et de l'espace euclidien. Traditionnellement définies par des équations, elles s'obtiennent toutes, au même titre que les polyèdres, à partir d'un « patron » plan et d' « instructions de collage ». C'est là le mode de définition général des variétés.
Il est difficile de dire qui le premier a étudié les courbes ou les surfaces. Gauss disposait de la notion de surface abstraite, mais la notion générale de variété en dimension quelconque est due à Bernhard Riemann. Les variétés se sont imposées comme le cadre naturel de nombreux problèmes de mathématiques et de physique, permettant de travailler dans un cadre plus vaste que celui, trop étroit, fourni par les espaces vectoriels. On donne parfois à ces derniers le nom d’espaces plats ou d’espaces euclidiens pour les distinguer des espaces courbes que sont les variétés.
La topologie algébrique cherche à classer les variétés (mais aussi des objets plus généraux) en en déterminant des invariants, c'est-à-dire des objets mathématiques - qui peuvent être des nombres réels - associés à chaque variété et qui en caractérisent la topologie. Certaines variétés sont munies de structures plus fortes : il est du ressort de la topologie différentielle, puis de la géométrie différentielle, de la géométrie riemannienne et de la géométrie symplectique de les étudier et de les classifier. Ces domaines sont encore aujourd'hui l'objet de nombreux travaux de recherches.
Les variétés constituent à la fois un cadre et un sujet d'étude communs pour les chercheurs en mathématiques et en physique. Elles se sont avérées les bons outils de travail pour formaliser la relativité générale d'Einstein et ont fortement servi dans la physique post-newtonienne, dont la théorie des cordes, la théorie des membranes, ... Les variétés sont devenues tout aussi utiles (voire indispensables) dans des travaux récents de mécanique classique.
Introduction
Les difficultés qui existent pour représenter sur un plan une surface sphérique comme la Terre, sont un bon moyen d'appréhender la géométrie différentielle. C'est aussi la raison pour laquelle le vocabulaire de cette branche des mathématiques emprunte beaucoup à celui de la cartographie.
Les cartes
On se déplace sur la sphère terrestre en utilisant des cartes géographiques planes, rassemblées en un atlas. Au bord d'une carte figure l'information nécessaire pour y « recoller mentalement » la carte suivante. Pour opérer ce recollement, une certaine redondance dans l'information est nécessaire : ainsi la carte de l'Europe et celle de l'Asie peuvent toutes deux contenir Moscou. De manière similaire, il est possible de décrire une variété en utilisant une collection de cartes, réunies en un atlas mathématique, indiquant comment passer d'une carte à l'autre. Le globe terrestre fournit un exemple typique de variété, puisqu'il peut être représenté par une collection de cartes géographiques.
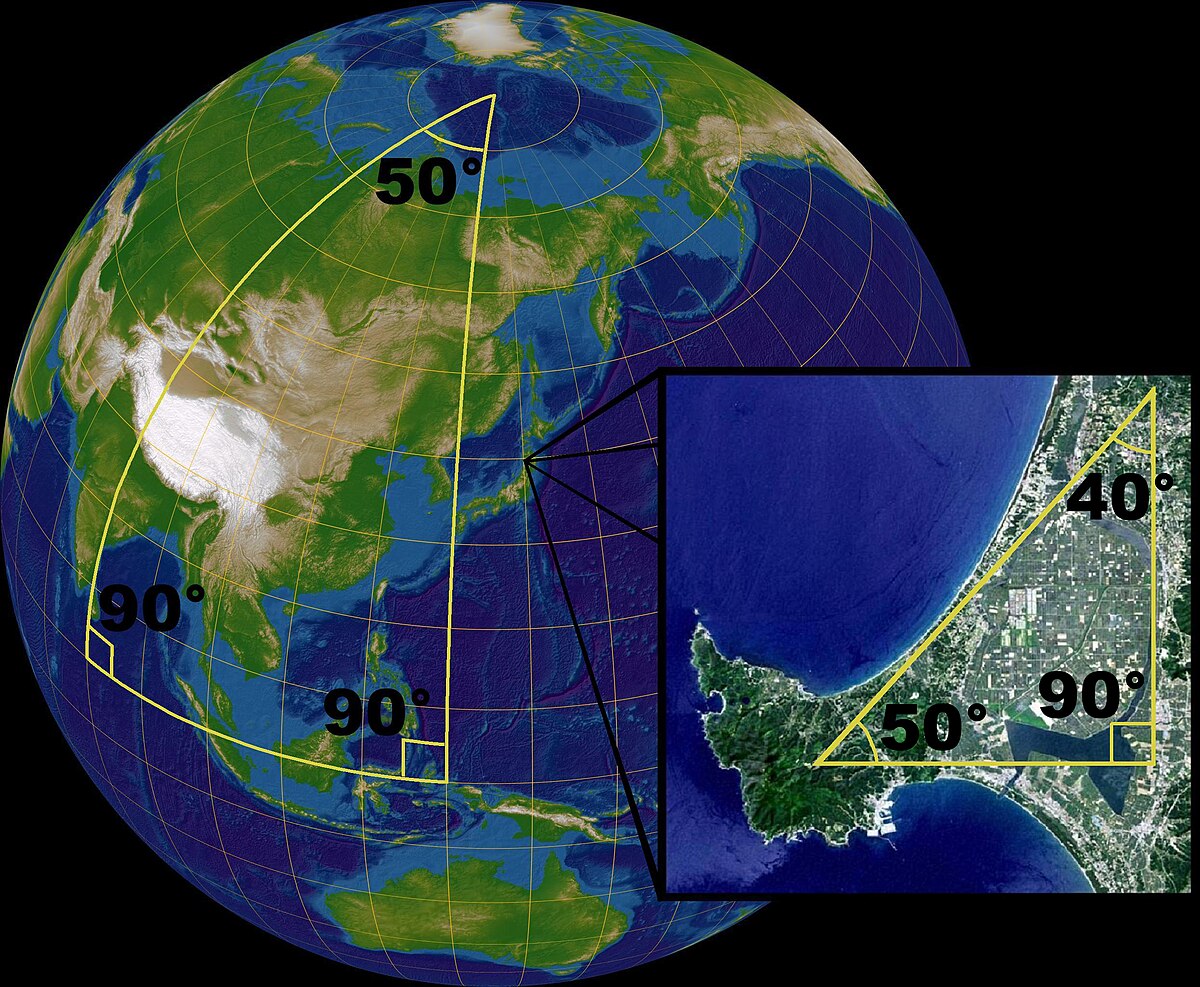
Une carte est une portion de la variété analogue à une portion d'espace vectoriel ; les changements de cartes indiquent comment ces portions de variétés se raccordent entre elles. Ainsi, pour décrire un cercle il est possible de prendre comme cartes deux arcs qui se chevauchent ; le changement de cartes constitue une information sur le recollement au niveau de la zone de chevauchement.
Il n'est généralement pas possible de décrire une variété à l'aide d'une seule carte, parce que la structure globale de la variété est différente de la structure simple de l'espace modèle. Par exemple, aucune carte « plate » ne peut décrire convenablement la Terre entière. Les variétés apparaissent comme des espaces topologiques et leurs topologies sont uniquement déterminées par la donnée de leurs atlas respectifs.
Suivant la nature des applications de changement de cartes, la variété possède une structure plus ou moins forte : variété topologique, variété différentielle, variété symplectique, variété localement plate par exemple. Pour une variété topologique, la donnée d'un atlas équivaut simplement à la donnée d'une topologie dont les ouverts suffisamment petits s'identifient à l'espace plat. Pour les structures plus fines citées, l'introduction de cartes est indispensable pour les définir.
La dimension et la topologie
La première notion attachée à une variété est sa dimension. Elle désigne le nombre de paramètres indépendants qu'il faut se fixer pour positionner localement un point sur la variété.
- Les courbes sont des variétés de dimension un puisque l'abscisse curviligne par exemple suffit à décrire la position.
- Sur une surface, il faut deux coordonnées : ainsi sur une sphère il faudra préciser latitude et longitude, comme c'est le cas pour indiquer l'emplacement d'une ville sur le globe terrestre.
- Il existe de nombreuses variétés de dimension supérieure à deux, qu'il est difficile de représenter graphiquement. Elles ne peuvent en effet se représenter dans notre espace environnant, qui est de dimension trois (largeur, longueur, hauteur).
Toutes les variétés de même dimension n — ou n-variétés — ont la même topologie locale. Par définition, une petite portion de ces variétés ressemble toujours à un espace vectoriel réel de dimension n. Ainsi une petite portion de courbe est l'analogue courbe d'une droite, une petite portion de surface l'analogue courbe d'un plan, et ainsi de suite.
En revanche, les variétés se distinguent par leur aspect global. Par exemple sur la figure ci-contre, la variété rouge est formée de deux morceaux bornés (deux cercles), et il est visiblement impossible de déformer continûment celle-ci pour obtenir une des trois autres courbes.
Autre exemple, une sphère et un tore ne se ressemblent pas topologiquement. Tout cercle tracé sur une sphère la sépare en au moins deux morceaux disjoints ; cependant, il existe de nombreux cercles tracés sur un tore qui ne le séparent pas en morceaux disjoints. Plus généralement, la topologie peut se compliquer par la présence de « trous », d' « anses », etc.
Variété abstraite et sous-variété
De nombreux sous-ensembles particuliers du plan, de l'espace de dimension 3 peuvent être naturellement munis d'une structure de variétés : le cercle, le cylindre, la sphère, le ruban de Möbius etc. On les appelle sous-variétés ou variétés plongées. Il existe en outre une notion de variété abstraite, qui sont construites sans qu'on les considère comme une sous-variété. L'exemple le plus simple est l'espace projectif de dimension n : c'est simplement l'ensemble de toutes les droites passant par l'origine dans un espace vectoriel de dimension n+1. Un autre exemple est la bouteille de Klein, représentée ci-contre de façon imparfaite. Pour mieux l'appréhender visuellement, il faut imaginer un artisan verrier prenant une bouteille ordinaire, perçant son fond, allongeant le goulot, le courbant, et le faisant pénétrer magiquement à travers un côté de la bouteille pour le relier au fond. Elle peut être décrite par un système de cartes, et de coordonnées figuré par le maillage de méridiens et de parallèles ci-contre.
Le théorème de plongement de Whitney montre que toute variété abstraite de dimension n peut être réalisée comme sous-variété d'un espace de dimension suffisamment grande, à savoir de dimension 2n. Ainsi la bouteille de Klein ne peut être plongée dans l'espace à trois dimensions, mais forme une sous-variété de l'espace à quatre dimensions.
L'introduction des variétés abstraites peut paraître superfétatoire au premier abord. Cependant, s'affranchir de la considération de l'« espace ambiant », celui dans lequel est plongée la variété, peut aussi présenter des avantages. En particulier, de nombreux modes de construction de nouvelles variétés à partir de variétés déjà définies, à l'exemple des quotients et des recollements topologiques (voir plus loin), ne font intervenir que les variétés elles-mêmes, et (surtout) pas l'espace qui pourrait éventuellement les entourer. Quand bien même en théorie il est possible de les réaliser comme sous-variétés d'un espace vectoriel, il ne serait pas judicieux de le faire en pratique, et cela ne présenterait aucun intérêt.