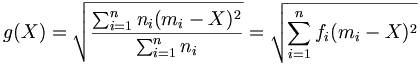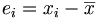Critères de dispersion - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs est disponible ici.

Cet article fait partie de la série
Mathématiques élémentaires

Algèbre

Analyse

Arithmétique

Géométrie

Logique

Probabilité

Statistique

Après avoir déterminé où se situent les valeurs du caractère statistique en cherchant des critères de position, on peut chercher à déterminer la dispersion de ces valeurs.

En mesure physique (métrologie), cette dispersion est estimée par l'écart type, qui sert à calculer l'erreur de mesure. De manière plus générale, il est important de savoir si les valeurs sont groupées ou au contraire dispersées, ce qui indique si la population est uniforme ou pas vis-à-vis du critère testé.

Étendue

L'étendue est la différence entre la valeur maximale et la valeur minimale du caractère statistique.

étendue =

x m a x - x m i n

Écart interquartile

L'écart inter-quartile est la différence entre le troisième et le premier quartile.

écart interquartile = Q3 - Q1

L'écart interquartile correspond à l'étendue de la série statistique après élimination de 25% des valeurs les plus faibles et de 25% des valeurs les plus fortes.

Dispersion autour de la moyenne

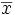
Après avoir calculé la moyenne, $\overline{x}$ , on peut chercher à savoir de quelle façon les valeurs s'éloignent de cette moyenne. On crée alors une nouvelle série statistique: la série des écarts.

Ecart moyen

Le premier réflexe serait de calculer la moyenne de ces écarts. Mais les propriétés de la moyenne nous assurent que la moyenne des écarts est nulle. En effet, certains de ces écarts sont négatifs et d'autres sont positifs, la somme des écarts positifs compensant exactement la somme des écarts négatifs. Il faut donc s'abstraire du signe et calculer alors la moyenne de la valeur absolue des écarts. C'est ce que l'on appelle l'écart moyen.

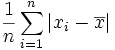
écart moyen = $\frac{1}{n}\sum_{i=1}^n|x_i-\overline{x}|$ dans le cas d'une série discrète non triée.
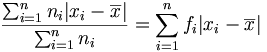
écart moyen = $\frac{\sum_{i=1}^nn_i|x_i-\overline{x}|}{\sum_{i=1}^nn_i}=\sum_{i=1}^nf_i|x_i-\overline{x}|$ dans le cas d'une série discrète regroupée.
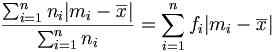
écart moyen = $\frac{\sum_{i=1}^nn_i|m_i-\overline{x}|}{\sum_{i=1}^nn_i}=\sum_{i=1}^nf_i|m_i-\overline{x}|$ dans le cas d'une série continue.

Variance

L'utilisation des valeurs absolues est souvent une impasse en mathématique (parce que la fonction valeur absolue n'est pas dérivable). Pour rendre positifs les écarts, un autre outil est à notre disposition: la mise au carré. On ne va donc pas calculer la moyenne des écarts mais la moyenne des écarts au carré. C'est ce qu'on appelle la variance :

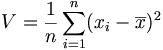
$V=\frac{1}{n}\sum_{i=1}^n(x_i-\overline{x})^2$ dans le cas d'une série discrète non triée.
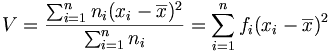
$V=\frac{\sum_{i=1}^nn_i(x_i-\overline{x})^2}{\sum_{i=1}^nn_i}=\sum_{i=1}^nf_i(x_i-\overline{x})^2$ dans le cas d'une série discrète regroupée.
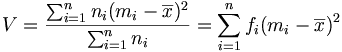
$V=\frac{\sum_{i=1}^nn_i(m_i-\overline{x})^2}{\sum_{i=1}^nn_i}=\sum_{i=1}^nf_i(m_i-\overline{x})^2$ dans le cas d'une série continue.

La disparition des valeurs absolues permet des calculs plus simples. On démontre que la variance peut se calculer plus simplement par les formules suivantes:

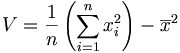
$V=\frac{1}{n}\left(\sum_{i=1}^nx_i^2\right)-\overline{x}^2$ dans le cas d'une série discrète non triée.
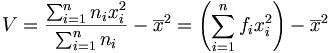
$V=\frac{\sum_{i=1}^nn_ix_i^2}{\sum_{i=1}^nn_i}-\overline{x}^2=\left(\sum_{i=1}^nf_ix_i^2\right)-\overline{x}^2$ dans le cas d'une série discrète regroupée.
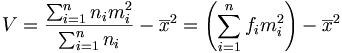
$V=\frac{\sum_{i=1}^nn_im_i^2}{\sum_{i=1}^nn_i}-\overline{x}^2=\left(\sum_{i=1}^nf_im_i^2\right)-\overline{x}^2$ dans le cas d'une série continue.

Ces formules étaient surtout utiles dans le cadre de calculs à la main ; l'usage des ordinateurs les rend un peu obsolètes...

Écart type

De par la mise au carré des écarts, l'unité de la variance est le carré de celle du caractère (si le caractère est en $k g$ , sa moyenne est en $k g$ mais sa variance est en $k g 2$ ) d'ou l'impossibilité d'additionner la moyenne et la variance. On a donc défini l'écart type noté $σ$ . L'écart type est la racine de la variance (et donc son unité est la même que celle de la moyenne. Cela a l'air anecdotique mais la possibilité d'additionner moyenne et écart type est fondamentale, en particulier pour le calcul d'intervalle de confiance (voir plus bas).

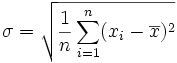
$\sigma=\sqrt{\frac{1}{n}\sum_{i=1}^n(x_i-\overline{x})^2}$ dans le cas d'une série discrète non triée.
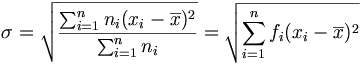
$\sigma=\sqrt{\frac{\sum_{i=1}^nn_i(x_i-\overline{x})^2}{\sum_{i=1}^nn_i}}=\sqrt{\sum_{i=1}^nf_i(x_i-\overline{x})^2}$ dans le cas d'une série discrète regroupée.
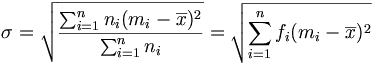
$\sigma=\sqrt{\frac{\sum_{i=1}^nn_i(m_i-\overline{x})^2}{\sum_{i=1}^nn_i}}=\sqrt{\sum_{i=1}^nf_i(m_i-\overline{x})^2}$ dans le cas d'une série continue.

Propriétés de l'écart type

Invariance par translation. L'écart type n'est pas modifié si on ajoute ou retranche une constante à la série statistique. Si $y i = x i + C$ alors $σ y = σ x$ .
Stabilité par multiplication par une constante. Si on multiplie une série par une constante positive, l'écart type est multiplié par la même constante. Si $y i = K x i$ alors $σ y = K σ x$ .
L'écart type est toujours positif et est nul si la série statistique est constante.
Sensibilité aux valeurs extrêmes. Comme la moyenne, l'écart type est sensible aux valeurs extrêmes ou aberrantes et il est parfois nécessaire d'éliminer ces valeurs avant de faire le calcul de l'écart type.

Écart type relatif

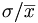
Pour comparer deux séries statistiques qui n'ont pas le même ordre de grandeur, il est parfois bon de comparer l'écart type et la moyenne en faisant le quotient, on obtient alors l'écart type relatif. $\sigma / \overline{x}$ .

Remarque l'écart type relatif est aussi appelé coefficient de variation

Intervalle de confiance ou plage de normalité

Lorsque le caractère statistique a une distribution normale gaussienne, grossièrement en forme de cloche, l'écart type prend tout son sens.

Dans l'intervalle $[\overline{x}-\sigma;\overline{x}+\sigma]$ , on trouve 68% de la population.
Dans l'intervalle $[\overline{x}-2\sigma;\overline{x}+2\sigma]$ , on trouve 95% de la population.
Dans l'intervalle $[\overline{x}-3\sigma;\overline{x}+3\sigma]$ , on trouve 99,7% de la population.

On appelle ces intervalles les plages de normalité à niveau de confiance de 68%, 95%, 99,7%.

Question de minimum

La médiane est la valeur qui rend minimum la fonction f définie par

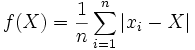
$f(X)=\frac{1}{n}\sum_{i=1}^n|x_i-X|$ dans le cas d'une série discrète triée non regroupée.

La moyenne est la valeur qui rend minimum la fonction g définie par

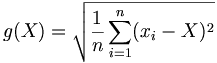
$g(X)=\sqrt{\frac{1}{n}\sum_{i=1}^n(x_i-X)^2}$ dans le cas d'une série discrète non triée.
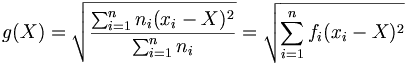
$g(X)=\sqrt{\frac{\sum_{i=1}^nn_i(x_i-X)^2}{\sum_{i=1}^nn_i}}=\sqrt{\sum_{i=1}^nf_i(x_i-X)^2}$ dans le cas d'une série discrète regroupée.
$g(X)=\sqrt{\frac{\sum_{i=1}^nn_i(m_i-X)^2}{\sum_{i=1}^nn_i}}=\sqrt{\sum_{i=1}^nf_i(m_i-X)^2}$ dans le cas d'une série continue.

Voici ce qui a causé les toutes premières inégalités de richesse 💰

Quelle est cette zone étrange dans l'Atlantique Nord ? 🌊

Cette planète orbite à angle droit autour de deux étoiles, une première ! 🔭

Des cellules solaires flexibles battent des records d'efficacité ⚡

Ce dispositif reproduit les trous noirs et trous blancs en laboratoire 🌀

Record établi pour un transistor en diamant 💎

Les sursauts radio rapides trahissent enfin leur origine cosmique 📡

Ces biomarqueurs sanguins prédisent la démence 10 ans à l'avance 🧠

Découverte majeure: des médicaments 23 fois plus efficaces contre le cancer 💊

Les oscillations collectives des foules humaines denses 🔁

Une forme inconnue de la matière détectée au LHC ? ⚛️

Le sel, un facteur méconnu de l'obésité ? 🧂

L'Univers en rotation, une réponse élégante à ce problème astrophysique majeur 🌀

Découverte tectonique majeure sous les Petites Antilles 🌍

Peut-on geler en chauffant ? ❄️

Une peau électronique pour doter les robots du sens du toucher 👌

Invention d'un bois semi-transparent avec une technique...surprenante ! 🌳

Le cancer inscrit dans nos gènes dès la naissance ? 🧬

Des supernovae à l'origine de deux extinctions massives sur Terre ? 💥

Le passé verdoyant du plus grand désert du monde 🐪

Après les campagnes antivaccins, la rougeole revient en force aux États-Unis 😷

Des puces quantiques plus proches que jamais ⚡

Pourrons-nous bientôt communiquer avec les dauphins grâce à l'IA ? 🐬

En déplaçant deux atomes, des chercheurs transforment le LSD en médicament surpuissant 💊

Des scientifiques parviennent à produire efficacement du carburant à partir de monoxyde de carbone 🛢️

Que nous apprend la découverte de cet insecte de 16 millions d'années ? 🐜

Avec 91km, l'accélérateur FCC fera passer le LHC pour un jouet ⚛️

Cette vitamine développe les fonctions cognitives du cerveau 🧠

Comment des impacts géants vaporisent les corps planétaires ☄️

Les Américains riches vivent moins longtemps que les Européens pauvres 💰

Attention à ce riz naturellement riche en arsenic 🍚

L'intelligence artificielle contre la mort subite 💀

L'inévitable formation d'un océan de magma basal sur Terre 🔥

Découverte d'une plante étrange sans chlorophylle 🌱

Existe-t-il des mélodies naturelles ? 🎶

Cette exoplanète présente une signature de vie bien plus forte que celle de la Terre 👽

L'origine énigmatique des rayons cosmiques les plus énergétiques ⚡

Le diagnostic de l'autisme remis en cause par l'intelligence artificielle 🩺

Imprimer en 3D avec la lumière du soleil ☀️

La pollution atmosphérique nuit gravement au cerveau 🧠

Le trou noir supermassif Ansky vient de se réveiller ⚫

Voici ce qui rend notre cerveau vraiment unique 🧠

Asymétrie matière-antimatière: une nouvelle pièce du puzzle dévoilée 🧩

Neige en inuit, goût en japonais... comment les langues décomposent la réalité ? 💬

La physique révèle les secrets d'un strike parfait au bowling 🎳

Le TDAH associé à la démence 🧠

Découverte d'une nouvelle forme d'intrication quantique, une première en 20 ans ⚛️

Le régime cétogène montre des surprises sur le cholestérol 🧐

Un tango observationnel révèle une Super-Terre 🔭

Cette expérience montre que la graisse brune augmente fortement la longévité 🕒

Page générée en 0.112 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise