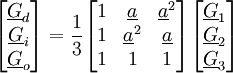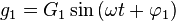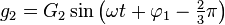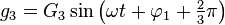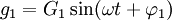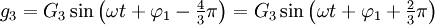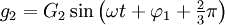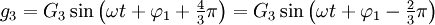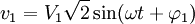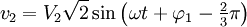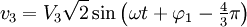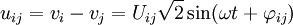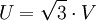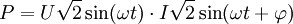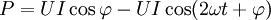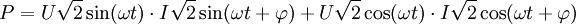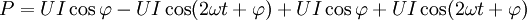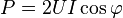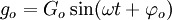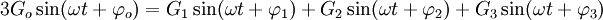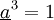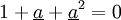Triphasé - Définition
Le triphasé est un système de trois tensions sinusoïdales de même fréquence qui sont déphasées entre elles (de 120 ° ou ?π radians dans le cas idéal). Si la fréquence est de 50 Hz par exemple, alors les trois phases sont retardées de ?50/3 seconde (soit 6,7 millisecondes). Lorsque les trois conducteurs sont parcourus par des courants de même valeur efficace, le système est dit équilibré.
Définitions de base
Grandeurs triphasées
Un système de grandeurs triphasées peut se mettre sous la forme :
Systèmes triphasés équilibrés et déséquilibrés
Un système de grandeurs (tensions ou courants) triphasées est dit équilibré si les 3 grandeurs, fonctions sinusoïdales du temps, ont la même amplitude : G1 = G2 = G3 = G
Dans le cas contraire, le système triphasé est dit déséquilibré
Systèmes triphasés directs et indirects
Si les 3 grandeurs passent par la valeur 0 dans l'ordre 1, 2, 3, 1, ..., le système triphasé est dit direct. Il peut alors se mettre sous la forme :
Si les 3 grandeurs passent par la valeur 0 dans l'ordre 1, 3, 2, 1, ..., le système triphasé est dit indirect. Il peut alors se mettre sous la forme :
Distribution triphasée
Une distribution triphasée comporte 3 ou 4 fils
- Trois conducteurs de phase
- Un conducteur de neutre qui n'est pas systématique mais qui est souvent distribué.
Tensions simples
Les différences de potentiel entre chacune des phases et le neutre constituent un système de tensions triphasées notées généralement V (V1N, V2N ,V3N) et appelées tensions simples ou tensions de phase. Mathématiquement, on peut noter :
Vi la valeur efficace, ω la pulsation, φi la phase à l'origine et t le temps.
Dans le cas de distributions équilibrées, on a V1 = V2 = V3 = V.
Tensions composées
Les différences de potentiel entre les phases constituent un système de tensions notées généralement U : (U12,U23,U31) et appelées tensions composées ou tensions de ligne.
Les tensions composées constituent un système de tensions triphasées si et uniquement si le système de tensions simples est un système équilibré. La somme des trois tensions composées est toujours nulle. Il en résulte que la composante homopolaire des tensions entre phases est toujours nulle (voir ci-dessous transformation de Fortescue)
Dans le cas de distributions équilibrées, on a :U12 = U23 = U31 = U
Relation entre tensions simples et composées
Dans le cas de distribution équilibrées, on a :
Intensités
Les courants de ligne sont notés I et les courants qui traversent un récepteur sont notés J (parfois appelés courant de phase). Dans un couplage dit 'étoile' I = J.
Dans un couplage dit 'triangle', il est nécessaire de décomposer chaque courant traversant les récepteurs. Ainsi on a:
- I1 = J21 + J31
- I2 = J23 − J21
- I3 = − J23 − J31
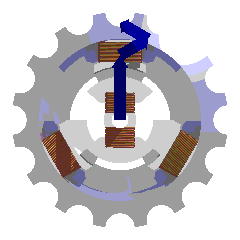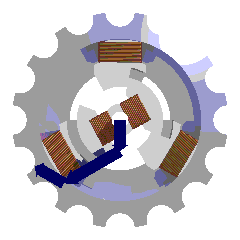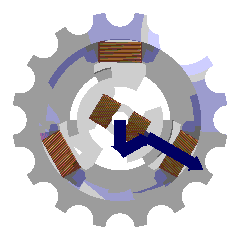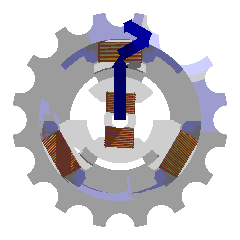
Récepteurs triphasés
Un récepteur triphasé est constitué de 3 dipôles. Si ces 3 dipôles sont absolument identiques, le récepteur est dit équilibré.
Un récepteur triphasé peut être relié à l'alimentation de 2 manières :
Un récepteur équilibré alimenté par un système équilibré de tensions absorbera 3 courants de ligne formant également un système triphasé équilibré.
Connexion d'un récepteur triphasé
Les trois dipôles qui constituent le récepteur triphasé sont reliés à 6 bornes conventionnellement disposées comme l'indique la figure ci-dessous.
L'avantage de cette disposition est de permettre la réalisation des deux couplages avec des barrettes d'égale longueur, la distance entre deux bornes contiguës étant constante. L'appareil est fourni avec trois barrettes identiques dont la longueur permet un câblage horizontal ou vertical. On doit utiliser ces barrettes de connexion afin de réaliser les couplages désirés :
Couplage étoile
Le couplage étoile des enroulements (couplage le plus fréquent) s'obtient en plaçant 2 barrettes de connexions de la manière suivantes :
Les 3 bornes restantes seront câblées avec les 3 conducteurs de phases.
Les 3 bornes reliées ensemble par les deux barrettes constituent un point qui sera au potentiel du neutre. Ce point peut être relié au neutre de la distribution, mais ce n'est pas une obligation, cela est même fortement déconseillé pour les machines électriques.
Couplage triangle
Le couplage triangle des enroulements s'obtient en plaçant 3 barrettes de connexions de la manière suivante :
Un câble de phase est relié ensuite à chaque barrette. Le câble de neutre n'est pas connecté.
Plaques signalétiques des récepteurs triphasés
La plaque signalétique d'un récepteur triphasé précise la valeur des deux tensions entre phases permettant de l'alimenter :
- Exemple
- Chauffe eau : 230 / 400 :
- La première valeur est la tension entre phase requise pour câbler le récepteur en triangle
- La deuxième valeur est la tension entre phase requise pour câbler le récepteur en étoile
Puissance consommée par un récepteur triphasé
Puissance active
Le théorème de Boucherot impose que cela soit la somme des puissances consommées par chacun des dipôles :
- en étoile :
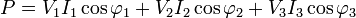
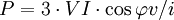
- en triangle :

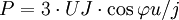
- Pour les récepteurs équilibrés et quel que soit le couplage, on peut écrire :
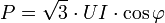
- Remarque : Dans ce cas,

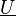
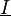
Intérêt du triphasé
Intérêt pour le transport de l'électricité
Le transport en triphasé permet d’économiser du câble et de diminuer les pertes par effet joule : 3 fils de phases suffisent (le neutre n'est pas transporté, il est "recréé" au niveau du dernier transformateur). En effet, le déphasage entre chaque phase est tel que, pour un système équilibré, la somme des trois courants est supposée nulle (si les trois courants ont la même amplitude, alors
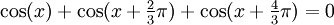
Intérêt pour la production de l'électricité
De meilleurs alternateurs
L'alternateur triphasé s'est imposé dès l'origine (avant 1900) comme le meilleur compromis[1].
Plus de 95 % de l’énergie électrique est produite par des alternateurs synchrones, des machines électromécaniques fournissant des tensions de fréquences proportionnelles à leur vitesse de rotation. Ces machines sont moins coûteuses et ont un meilleur rendement que les machines à courant continu (dynamos) qui délivrent des tensions continues (95 % au lieu de 85 %).
Les alternateurs (machines synchrones) triphasés qui produisent l'énergie électrique ont un meilleur rendement et un meilleur rapport poids/puissance qu'un alternateur monophasé de même puissance.
Annuler la puissance fluctuante
Supposons qu'un alternateur monophasé délivre 1000 A sous une tension de 1000 V et de fréquence 50 Hz. L'expression de la puissance délivrée se met sous la forme :
Donc la puissance active délivrée (le premier terme de la somme) est comprise entre 0 et 1 MW (elle dépend du facteur de puissance de la charge), mais la puissance fluctuante (le deuxième terme de la somme) est une puissance sinusoïdale de fréquence 100 Hz et d’amplitude obligatoirement égale à 1 MW. La turbine, du fait de son inertie, tourne avec une vitesse mécanique quasi constante, et donc à chaque instant elle fournit une puissance identique. Ces différences de puissance se traduisent par des oscillations de couples qui sont, en majeure partie, absorbées par l’élasticité de l’arbre de transmission et finissent par provoquer sa destruction.
Pour supprimer cette puissance fluctuante, les alternateurs de grande puissance doivent donc nécessairement produire un système de tensions polyphasées : il faut produire n phases (n ≥ 2) déphasées convenablement dans le temps.
Par exemple en diphasé:
La puissance fluctuante a bien été annulée.
Le choix qui a été fait pour l'ensemble des réseaux du monde est n = 3.
Transformation de Fortescue
Tout système de grandeurs triphasées déséquilibré peut se mettre sous la forme de la somme de trois systèmes équilibrés :
- Un système équilibré direct noté Gd.
- Un système équilibré inverse noté Gi.
- Un sytème de tension homopolaire noté Go (en réalité une grandeur monophasée que l'on divise en 3 pour le calcul matriciel).
Systèmes triphasés homopolaires
Comme expliqué précédemment, ce n'est pas vraiment un système triphasé car cela correspond à un système de 3 tensions en phase :
L'intérêt de cette décomposition est de faciliter l'écriture matricielle de la transformation de Fortescue.
Matrice de transformation
Le but est de trouver les valeurs de Gd, Gi et Go à partir de G1, G2 et G3.
Calcul de Go
Comme la somme des trois grandeurs d'un système équilibré est nulle, on à forcément :
Opérateur de rotation : a
- Remarque : Une grandeur soulignée représente le nombre complexe associé à la grandeur sinusoïdale considérée.
C'est un nombre complexe de module 1 et d'argument
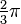
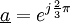
Le résultat de sa multiplication au nombre complexe associé à une grandeur correspond à une autre grandeur de même amplitude et déphasée de
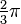
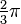
Il vérifie les propriétés suivantes :
Matrice de Fortescue