Icosaèdre - Définition
 |
|
| Type | Polyèdre régulier |
|---|---|
| Faces | Triangle |
| Éléments : · Faces · Arêtes · Sommets · Caractéristique |
20 30 12 2 |
| Faces par sommet | 5 |
| Sommets par face | 3 |
| Isométries | Ih |
| Dual | Dodécaèdre |
| Propriétés | Deltaèdre régulier et convexe |
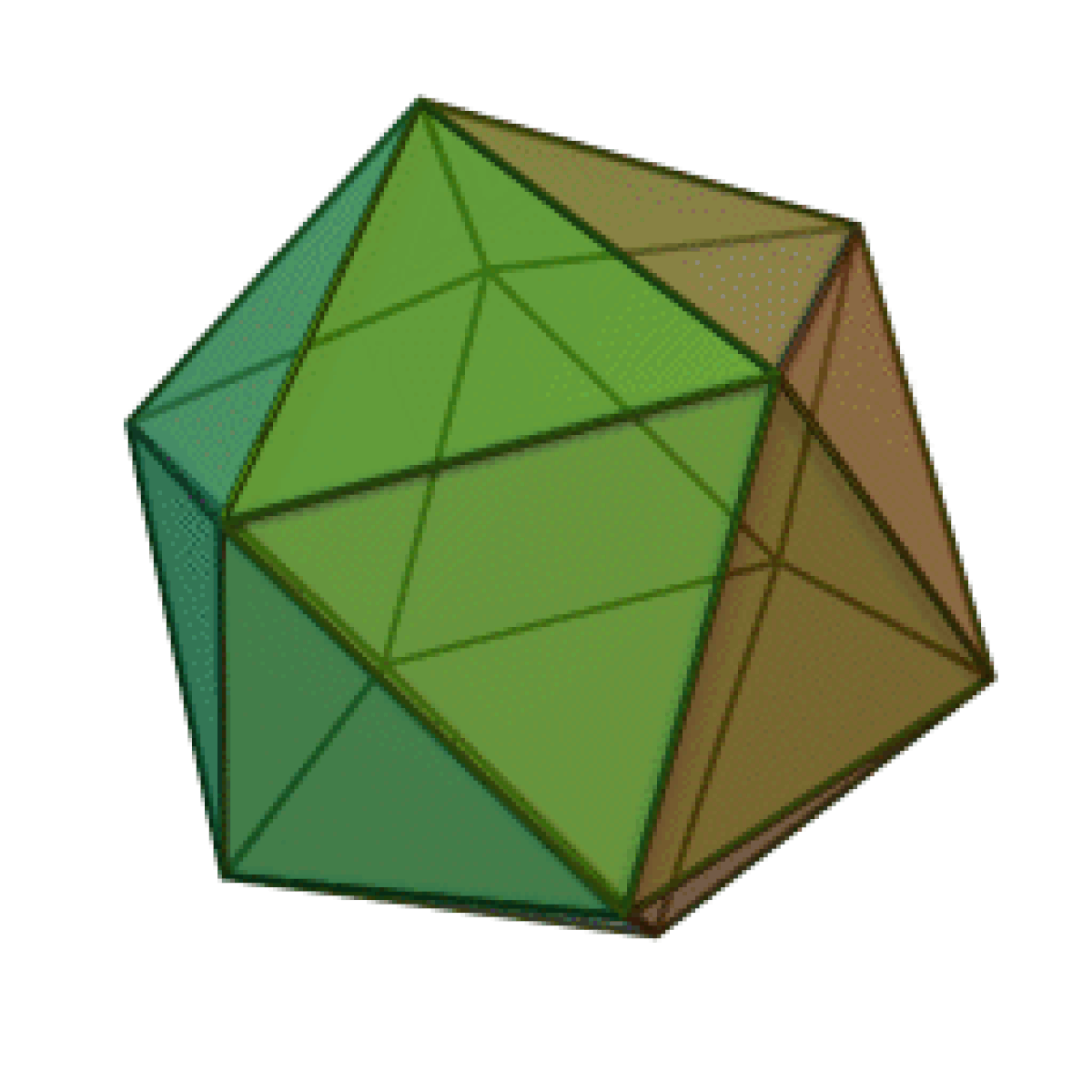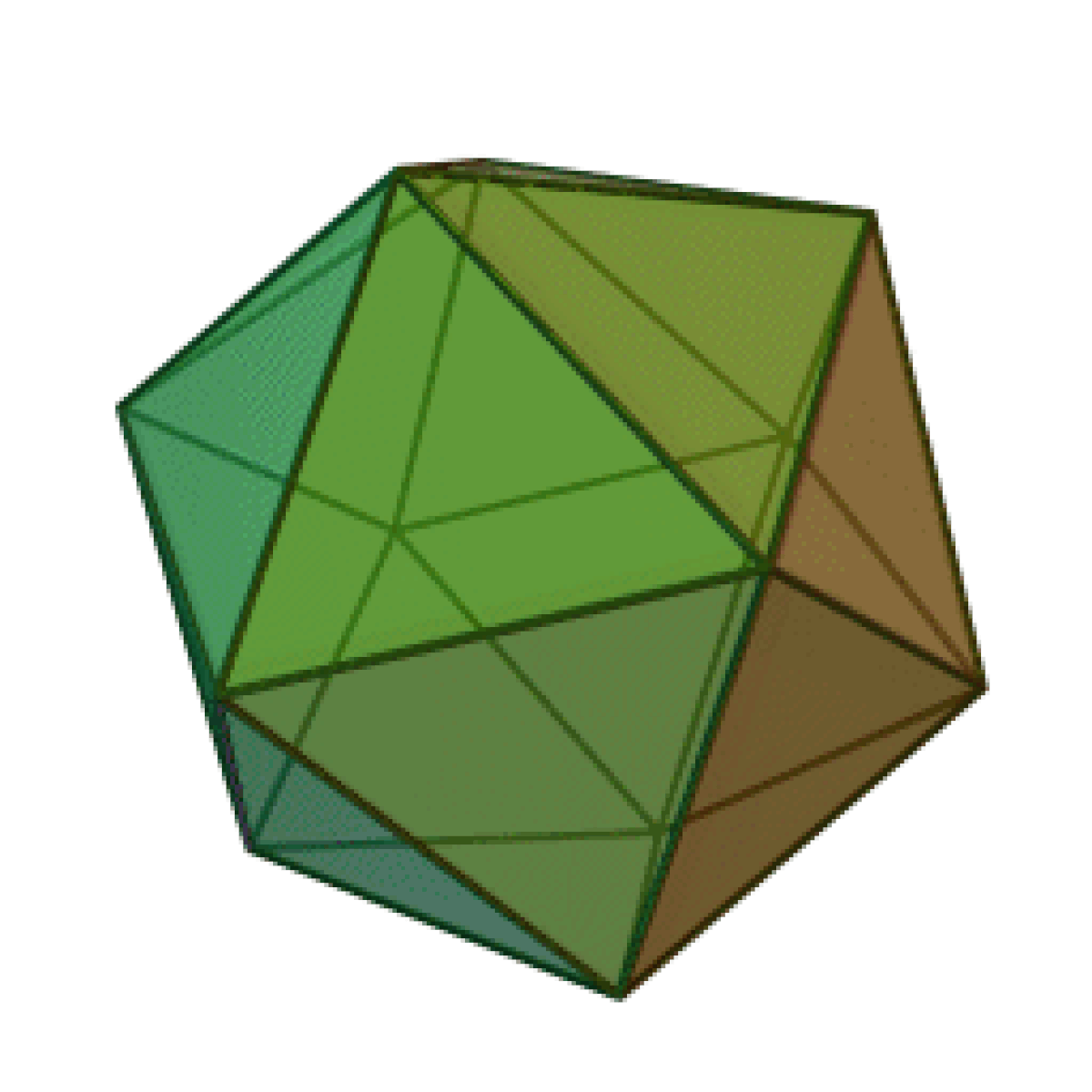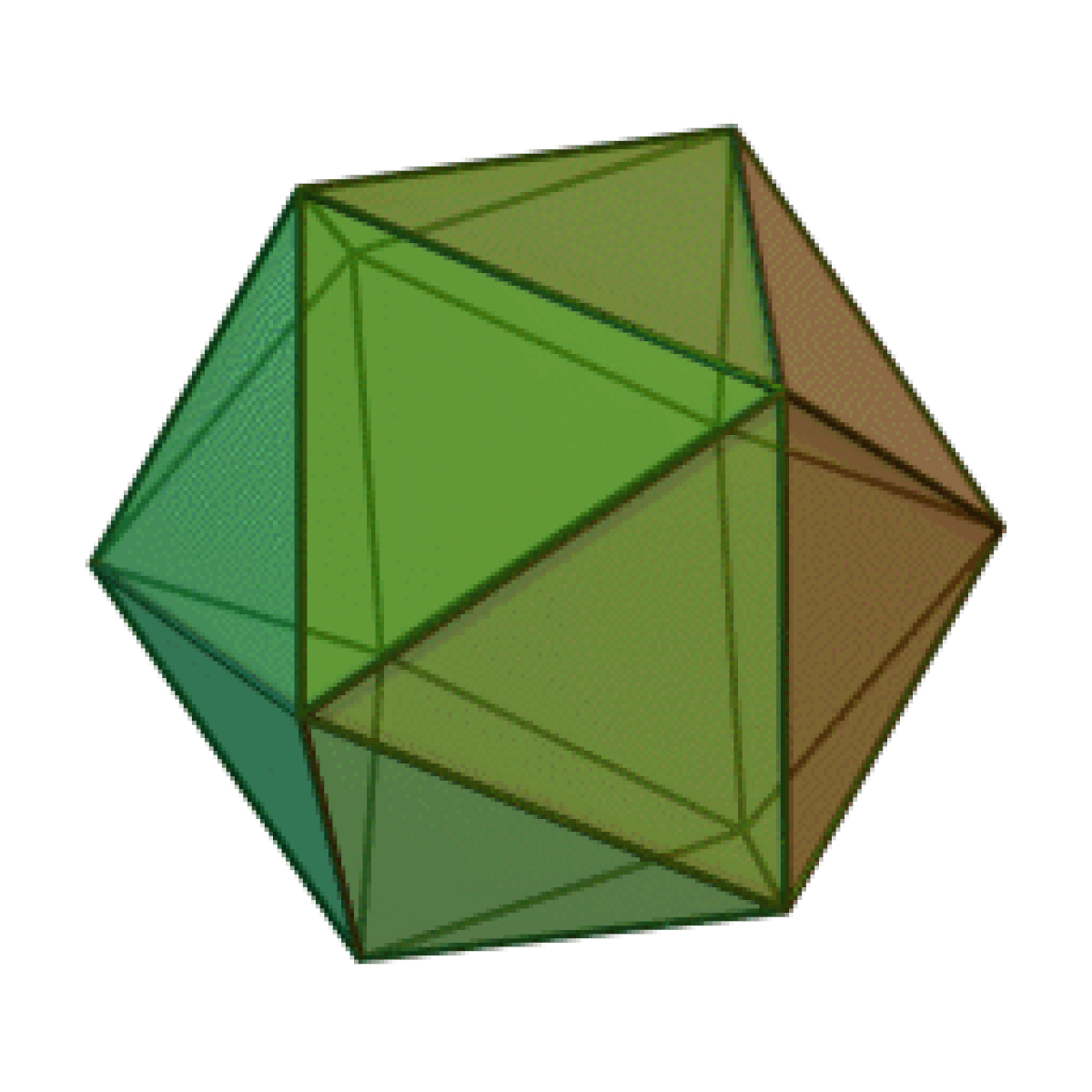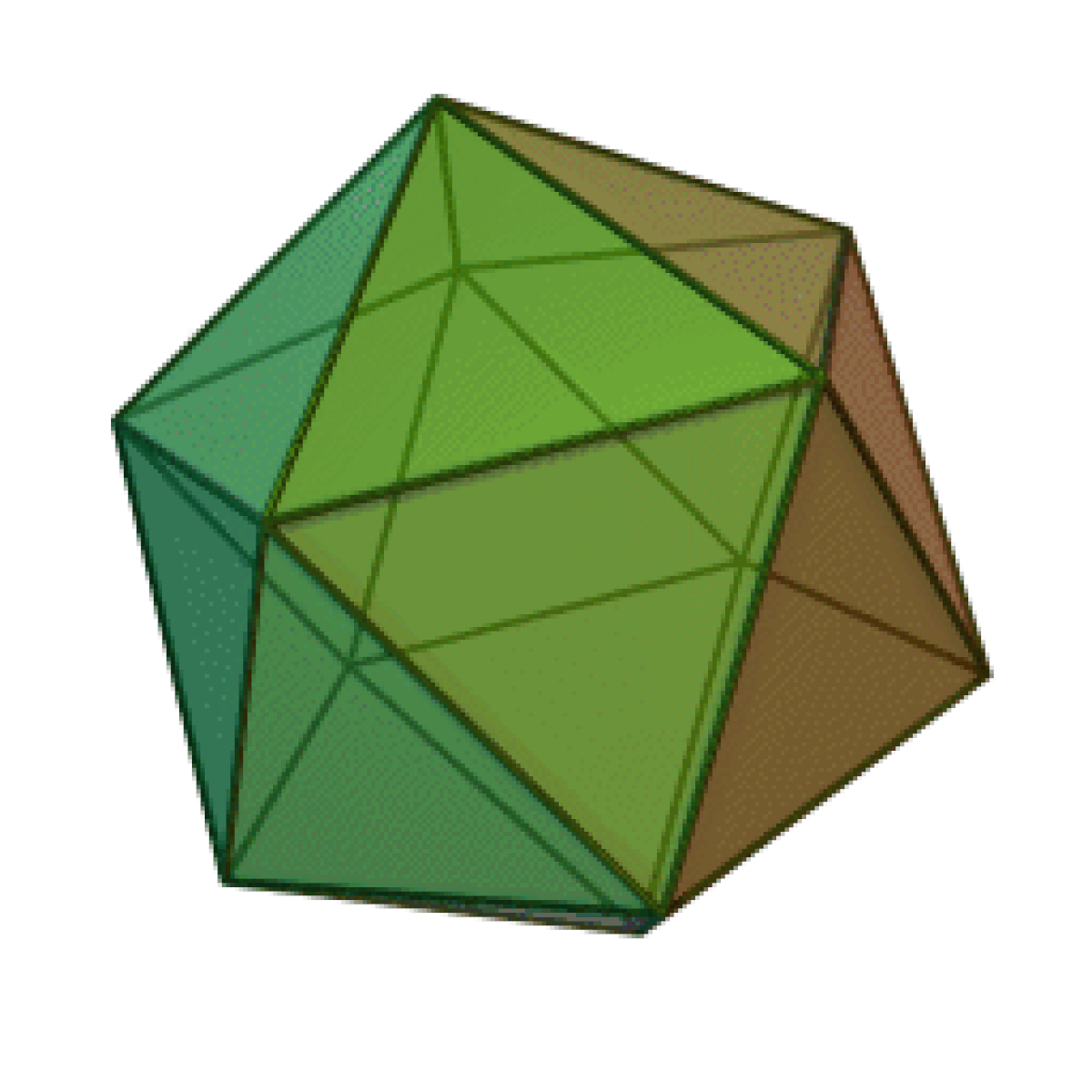
Un icosaèdre est un polyèdre à 20 faces. Le préfixe icosa-, d'origine grecque, fait référence au nombre de faces.
Icosaèdre régulier
L'icosaèdre régulier est le cinquième solide de Platon, polyèdre composé de 12 sommets et de 20 faces, chacun étant un triangle équilatéral, et dont 5 se rejoignent à chaque sommet. C'est le polyèdre régulier convexe ayant le plus grand nombre de faces.
L'angle dièdre est 138° 11' 32.
Si a est la longueur d'une arête :
- La surface vaut :
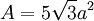
- La hauteur vaut :
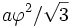
- Le rayon de la sphère inscrite est :
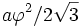
- Le rayon de la sphère circonscrite est :
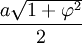
où
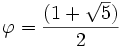
- Le volume vaut :
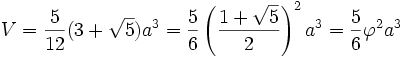
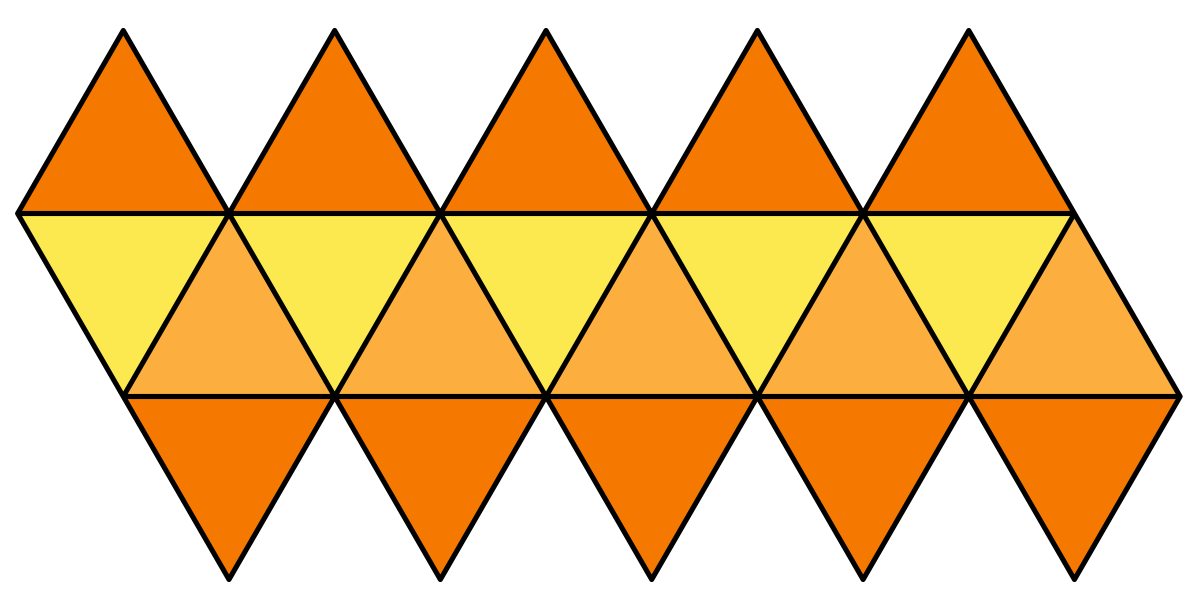
Patrons de l'icosaèdre régulier
Groupe d'isométries de l'icosaèdre régulier
Fascination de l'icosaèdre
Dans certains jeux de rôle, le dé à 20 faces (abrégé d20) est utilisé pour déterminer le succès ou l'échec d'une action. Ce dé est un icosaèdre.
En biologie moléculaire, beaucoup de virus, comme le virus de l'Herpès, ont la forme d'un icosaèdre. Les structures virales sont formées de sous-unités protéiques identiques répétées, et la forme d'un icosaèdre est la forme la plus adaptée pour assembler ces sous-unités, car elle permet un espace maximal pour le génome viral. En effet, parmi les solides de Platon, l'icosaèdre optimise la place occupée dans la sphère circonscrite.
En remplaçant chaque face de l'icosaèdre par une résistance de 1 ohm, la mesure de la résistance entre deux coins opposés donne 0.5 ohms, et entre deux coins adjacents 11/30 ohms.
La projection de Fuller (ou carte Dymaxion, crée par Richard Buckminster Fuller) est une projection gnomonique sur un icosaèdre.
Icosaèdre et dodécaèdre
En dépit des apparences, un icosaèdre inscrit dans une sphère occupe moins d'espace (60,54%) qu'un dodécaèdre inscrit dans une sphère (66,49%).

















































