Géométrie non euclidienne - Définition
On nomme géométrie non euclidienne une théorie géométrique modifiant au moins un des axiomes postulés par Euclide dans les Éléments.
Les différentes géométries non euclidiennes sont issues de la volonté de démontrer le cinquième postulat (le postulat, après que les quatre autres aient été déclarés des axiomes) qui semblait peu satisfaisant car trop complexe, et peut-être redondant. Ce à quoi Saccheri, procédant par l'absurde, avait échoué à la fin du XVIIe siècle.
Dans les Éléments d'Euclide, le postulat ressemble à la conclusion d'un théorème, mais qui ne comporterait pas de démonstration : Si une droite, tombant sur deux droites, fait les angles intérieurs du même côté plus petits que deux droits, ces droites, prolongées à l'infini, se rencontreront du côté où les angles sont plus petits que deux droits, et qu'on peut comprendre comme : Par un point extérieur à une droite, il passe toujours une parallèle à cette droite, et une seule.
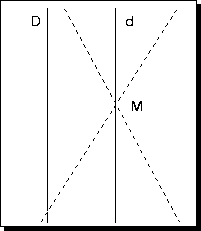
La droite d est la seule droite passant par le point M et parallèle à la droite D. Tout autre droite passant par M (comme par exemple les droites tracées en pointillée) est sécante avec D.
Durant plusieurs siècles, la géométrie euclidienne a été utilisée sans que l'on mette en doute sa validité. Elle a même été longtemps considérée comme l'archétype du raisonnement logico-déductif. Elle présentait en effet l'avantage de définir les propriétés intuitives des objets géométriques dans une construction mathématique rigoureuse.
Le développement des géométries non-euclidiennes
Les géométries à N - dimensions et les géométries non-euclidiennes sont deux branches séparées de la géométrie, qui peuvent être combinées, mais pas obligatoirement. Une confusion s'est établie dans la littérature populaire à propos de ces deux géométries. Parce que la géométrie euclidienne était à trois dimensions, on en concluait que les géométries non-euclidiennes comportaient nécessairement des dimensions supérieures.
C'est Gauss qui en 1824 avait formulé la possibilité qu'il existe des géométries alternatives à celles d'Euclide. On distingue les géométries à courbure négative, comme celle de Nicolaï Lobatchevsky (1829) et Bolyai (1832) (somme des angles d'un triangle inférieure à 180°, nombre infini de parallèles possibles à une droite par un point), des géométries à courbure positive comme celle de Riemann (1867) (somme des angles d'un triangle supérieure à 180°, parallèles se rejoignant aux pôles). La géométrie communément appelée " géométrie de Riemann " est un espace sphérique à trois dimensions, espace fini et cependant sans bornes,à courbure régulière, alternative au postulat euclidien des parallèles. Riemann a conçu par ailleurs une théorie étendue des géométries non-euclidiennes à N - dimensions (conférence de 1854).
L'idée de "géométrie non-euclidienne", sous-entend généralement l'idée d'un espace courbe, mais la géométrie d'un espace courbe n'est qu'une représentation de la géométrie non-euclidienne précise Sommerville dans "Les éléments de la Géométrie Non-Euclidienne" (Londres 1914). Il existe des espaces non-euclidiens à trois dimensions.
Les différents types de géométrie non euclidienne
La géométrie hyperbolique
Lobatchevsky, Felix Klein et Henri Poincaré ont créé des modèles de géométrie dans lesquelles on peut tracer une infinité de parallèles à une droite donnée et passant par un même point.
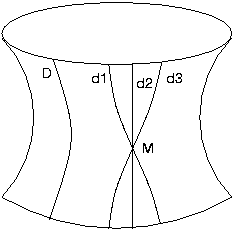
Il existe une infinité de droites qui comme d1, d2 et d3 passent par le point M et sont parallèles à la droite D.
Hormis le cinquième postulat, ces géomètries respectent toutes les autres définitions d'Euclide. Une droite est toujours définie comme la ligne de plus court chemin joignant deux points sur une surface. Il existe plusieurs modèles de géométrie hyperbolique à deux dimensions : le disque de Poincaré, le demi-plan de Poincaré, ...
La géométrie elliptique
Riemann a introduit un autre modèle de géométrie non euclidienne, la géométrie elliptique. Dans ce cas, par un point extérieur à une droite on ne peut mener aucune parallèle. Le modèle est très simple :
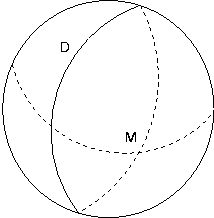
Il n'existe aucune droite passant par le point M et parallèle à la droite D.
- les points sont les paires de points antipodes d'une sphère.
- les droites sont les grands cercles (c'est-à-dire dire les cercles ayant le même centre que la sphère).
Espace géométrique, espace représentatif chez Poincaré
" L'espace moteur aurait autant de dimensions que nous avons de muscles " Cette affirmation de Poincaré dans La science et l'hypothèse est la marque de distinction la plus claire entre les deux sortes d'espace qu'il envisage, l'espace géométrique et l'espace représentatif.
Espace géométrique
Pour Poincaré, l’espace géométrique possède les propriétés suivantes:
- Il est continu
- Il est infini
- Il a trois dimensions
- Il est homogène, c’est-à-dire que tous ses points sont identiques entre eux
- Il est isotrope, c’est-à-dire que toutes les droites qui passent par un même point sont identiques entre elles.
Espace représentatif
Chez Poincaré, l'espace représentatif se manifeste sous une triple forme: l'espace visuel pur, l'espace tactile, l'espace moteur.
Les caractéristiques de l'espace représentatif sont les suivantes :
"Il n'est ni homogène, ni isotrope, on ne peut même pas dire qu'il ait trois dimensions." Pour Poincaré, nos représentations ne sont que la reproduction de nos sensations (visuelles, tactiles, motrices). Nous ne nous représentons donc pas les corps extérieurs dans l'espace géométrique (continu, infini, homogène, isotrope, à trois dimensions), mais nous raisonnons sur ces corps, comme s'ils étaient situés dans l'espace géométrique. "Il nous est aussi impossible de nous représenter les corps extérieurs dans l'espace géométrique qu'il est impossible à un peintre de peindre, sur un tableau plan, des objets avec leurs trois dimensions." " Les axiomes géométriques ne sont (donc) ni des jugements synthétiques a priori, ni des faits expérimentaux. Ce sont des conventions, ... des définitions déguisées... Une géométrie ne peut pas être plus vraie qu'une autre, elle peut simplement être plus commode. "
La quatrième dimension chez Poincaré
Pour Poincaré, l’accès à des objets à quatre dimensions ne saurait être que fortuit et notre base perceptive reste l’espace à 3 dimensions : "Une expérience quelle qu'elle soit, comporte une interprétation dans l'hypothèse euclidienne ".
Si Poincaré envisage un "solide invariable à quatre dimensions", le temps comme quatrième dimension, notion qui existe déjà chez d'Alembert dans son Encyclopédie de 1754, sera surtout développée chez Einstein avec le continuum d'espace-temps pseudo-euclidien de Minkowski (espace quadridimensionnel rigide).
Un tel espace-temps peut contenir le devenir d'un être à trois dimensions dans la relativité restreinte, puis variété pseudo-riemannienne avec ses systèmes de coordonnées curvilignes d'espace et de temps en relativité générale[1]. Son intersection avec un espace tridimensionnel donne le "présent" d'un univers[2].

















































