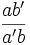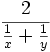Rapport anharmonique - Définition

Le rapport anharmonique ou birapport est un outil puissant dans la géométrie, en particulier la géométrie projective. Le nom de rapport anharmonique a été créé par Michel Chasles mais la notion lui est bien antérieure.

Rapport anharmonique de quatre points

Si ABCD sont quatre points distincts d'une droite (d) on appelle birapport ou rapport anharmonique de (A,B) et (C,D) le rapport des mesures algébriques suivant:

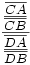
Les divisions sont supposées régulières. Le birapport de C,D par rapport à A, B est

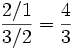
Les divisions sont supposées régulières. Le birapport de C, D par rapport à A, B est -1/3

Propriétés

Ce rapport est indépendant du repère choisi sur la droite (d) et de l'unité de longueur choisie.

Il est facile de voir que s'il on permute, en même temps A/B et C/D , on ne modifie pas le rapport anharmonique.

Ce rapport reste invariant pour de nombreuses transformations géométriques : isométrie, similitudes, transformation affine. La dualité par pôles et polaires réciproques conserve aussi le rapport anharmonique de quatre éléments d'une structure unidimensionnelle.

Il reste aussi invariant pour des homographies comme la projection centrale...

Si C est le barycentre de (A,a) et (B,b) et si D est celui de (A,a') et (B,b') alors le rapport anharmonique est

Ce qui explique d'ailleurs qu'une transformation conservant les barycentres conserve aussi les rapports anharmoniques

Rapport anharmonique de quatre droites concourantes

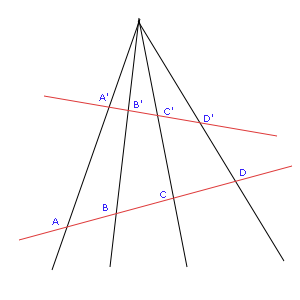
Un résultat important en géométrie projective stipule qu'une projection centrale conserve le rapport anharmonique . Il permet de dire dans la figure ci-jointe que les rapports anharmoniques de (A,B;C,D) et (A',B';C'D') sont égaux quelles que soient les droites qui portent la série des quatre points. (Une démonstration est réalisable en utilisant plusieurs fois le théorème de Thalès).

Puisque ce rapport est indépendant de la sécante aux quatre droites, ce rapport ne dépend que de la position relative des quatre droites. Il est alors appelé rapport anharmonique des droites

(d_A,d_B;d_C;d_D)

Voir Faisceau harmonique

Division harmonique

Lorsque le rapport anharmonique est égal à -1, on dit que les quatre points sont en division harmonique. Le point D est alors appelé le conjugué de C par rapport à A et B. On peut prouver que C est aussi le conjugué de D par rapport à ces même points.

Exemple 1: la suite harmonique

Le point d'abscisse 1/3 est le conjugué du point d'abscisse 1 par rapport aux points d'abscisse 0 et 1/2.

le point d'abscisse 1/4 est le conjugué de celui d'abscisse 1/2 par rapport aux points d'abscisse 0 et 1/3.

De manière générale, le point d'abscisse 1/(n+2) est le conjugué du point d'abscisse 1/n par rapport aux points d'abscisse 1/(n+1) et 0

On définit ainsi la suite de nombres 1, 1/2, 1/3, 1/4, ... appelée suite harmonique que l'on retrouve en musique pour définir la gamme harmonique

Exemple 2 : moyenne harmonique

Le conjugué de 0 par rapport à x et y est la moyenne harmonique de x et de y :

Exemple 3 : barycentre

Si C est le barycentre de (A,a) et (B,b) alors son conjugué par rapport à A et B est le barycentre de (A,-a) et (B,b)

Exemple 4 : bissectrices

Dans un triangle ABC, les bissectrices intérieure et extérieure issues de C coupent la droite (AB) en deux point D et E tels que A, B, D, E forment une divion harmonique

Exemple 5 : théorème d'Apollonius

L'ensemble des points M du plan tels que le rapport MA/MB est constant est un cercle de diamètre [CD] tel que A, B, C, D forment une division harmonique.

Exemple 6 : Polaire d'un point par rapport à deux droites

Rapport anharmonique, longueurs, aires et angles

Outre sa signification en termes de birapport de longueurs orientées, le rapport anharmonique concerne aussi les angles et les aires orientés. En effet l'aire des divers triangles tels que OAB peut s'exprimer de deux manières

- d'où, après simplifications de OH² ou de OA*OB*OC*OD l'égalité des 3 birapports: de longueurs, d'aires et de sinus.

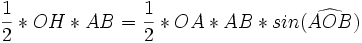
Rapport anharmonique sur un cercle

La propriété du birapport des sinus a une conséquence pour 6 points coycliques ABCDMP. Les angles et étant égaux ou supplémentaires, leurs sinus sont égaux. Le birapport des droites M(ABCD) est égal à celui des droites P(ABCD). En conséquence on peut parler du birapport de 4 points sur un cercle. On démontre, sans les sinus, en géométrie projective que cette propriété est vraie pour une conique quelconque (étant donnée une conique, si ABCDM sont fixes et si P parcourt la conique, alors le birapport des droites P(ABCD) est constant).

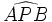
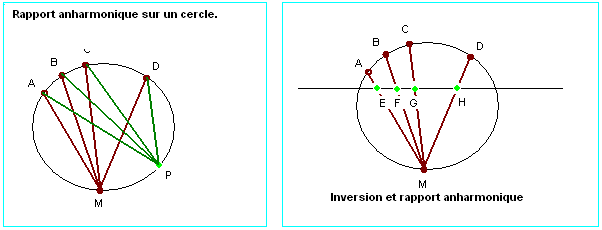
On peut en déduire que l'inversion de 4 points alignés, EFGH, de centre M, conserve leur birapport sur leurs images cocycliques ABCD.

Division harmonique, théorèmes de Ceva et de Ménélaüs

Le Théorème de Ceva et le Théorème de Ménélaüs sont reliés par un rapport harmonique.

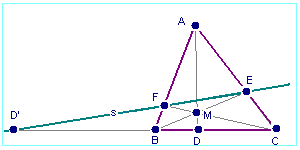
Les deux théorèmes impliquent deux relations :

et .

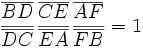
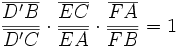
qui, après simplification, mènent à : , ce qui exprime une division harmonique. En passant cette propriété donne une construction du conjugué de D par rapport à BC, en prenant un point arbitraire A hors de (BC) et un point arbitraire M sur (AD).

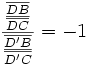
Voir quadrilatère complet