Méthode de Monte-Carlo - Définition

On appelle méthode de Monte-Carlo toute méthode visant à calculer une valeur numérique, et utilisant des procédés aléatoires, c'est-à-dire des techniques probabilistes. Le nom de ces méthodes fait allusion aux jeux de hasard pratiqués à Monte-Carlo.

Les méthodes de Monte-Carlo sont particulièrement utilisées pour calculer des intégrales en dimensions plus grandes que 1 (en particulier, pour calculer des surfaces, des volumes, etc.)

La méthode de simulation de Monte-Carlo permet aussi d'introduire une approche statistique du risque dans une décision financière. Elle consiste à isoler un certain nombre de variables-clés du projet telles que le chiffre d'affaires ou la marge... et à leur affecter une distribution de probabilités. Pour chacun de ces facteurs, on effectue un grand nombre de tirages aléatoires dans les distributions de probabilité déterminées précédemment, afin de déterminer la probabilité d'occurrence de chacun des résultats.

Le véritable développement des méthodes de Monte-Carlo s'est effectué, sous l'impulsion de John von Neumann et Stanislas Ulam notamment, lors de la Seconde Guerre mondiale et des recherches sur la fabrication de la bombe atomique. Notamment, ils ont utilisé ces méthodes probabilistes pour résoudre des équations aux dérivées partielles.

Théorie

Nous disposons de la définition de l'espérance mathématique d'une fonction g de variable aléatoire X, selon laquelle

f_X est la fonction de densité. Ceci peut être étendu aux probabilités discréte en sommant grâce à une mesure ν discréte, de type Dirac.

L'idée est de produire un échantillon (x₁,x₂,...,x_N) de la loi X, et de calculer un nouvel estimateur dit de Monte Carlo, à partir de cet échantillon.

Cet estimateur est construit à partir de la moyenne empirique, qui comme chacun sait est un estimateur sans biais de l'espérance:

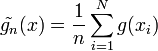
Ceci est l'estimateur de Monte Carlo. Nous voyons bien qu'en remplaçant l'échantillon par un ensemble de valeurs prises dans le support d'une intégrale, et de la fonction a intégrer, nous pouvons donc construire une approximation de sa valeur, construite statistiquement.

Exemples

Résolution du Problème du voyageur de commerce

La résolution du TSP demande du temps, et des algorithmes compliqués. La méthode de Monte-carlo peut fournir dans ce cadre une méthode de résolution efficace.

Détermination de la valeur de π (pi)

Cette méthode est proche de celle de Buffon.

Soit un point M de coordonnées (x,y) 0

On tire aléatoirement les valeurs de x et y.

Si x² + y² < 1 alors le point M appartient au disque de centre (0,0) de rayon 1.

La probabilité que le point M appartienne au disque est π/4.

En faisant le rapport du nombre de points dans le disque par rapport au nombre de tirage on obtient une approximation du nombre π/4 si le nombre de tirage est grand.

Détermination de la superficie d'un lac

Cet exemple est un classique en vulgarisation de la méthode de Monte-Carlo. Soit une zone rectangulaire ou carrée dont la longueur des côtés sont connus. Au sein de cette aire se trouve un lac dont la superficie est inconnue. Grâce aux mesures des côtés de la zone, on connaît l'aire du rectangle. Pour trouver l'aire du lac, on demande à une armée de tirer X coups de canon de manière aléatoire sur cette zone. On compte ensuite le nombre N de boulets qui sont restés sur le terrain, on peut ainsi déterminer le nombre de boulets qui sont tombés dans le lac : X-N. Il suffit ensuite d'établir un rapport entre les valeurs :

Par exemple, si le terrain fait 1000 m², que l'armée tire 500 boulets et que 100 projectiles sont tombés dans le lac alors la superficie du plan d'eau est de : 100*1000/500 = 200 m².

Bien entendu, la qualité de l'estimation s'améliore en augmentant le nombre de tirs et en s'assurant que les artilleurs ne visent pas toujours le même endroit mais couvrent bien la zone. Cette dernière remarque est à mettre en parallèle avec la qualité du générateur aléatoire qui est primordiale pour avoir de bons résultats dans la méthode de Monte-Carlo. Un générateur biaisé est comme un canon qui tire toujours au même endroit : les informations qu'il apporte sont réduites.

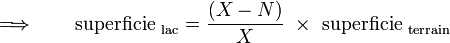
Application au modèle d'Ising