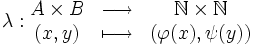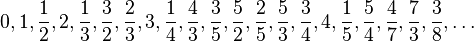Ensemble dénombrable - Définition
Un ensemble E est dit dénombrable s'il est équipotent à l'ensemble des entiers naturels



Naïvement, dire qu'un ensemble E est dénombrable signifie qu'il est possible de compter un à un chacun de ses éléments, et de leur attribuer un rang : on peut numéroter les éléments de E sans omission ni répétition, en utilisant tous les entiers naturels.
L'ensemble des entiers naturels est dénombrable, car un ensemble est toujours équipotent à lui-même, et tout ensemble équipotent à un ensemble dénombrable est lui-même dénombrable.
Un ensemble dénombrable est infini, car équipotent à

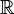
Vocabulaire
L'expression ensemble dénombrable a deux définitions :
- Certaines publications emploient cette expression non seulement dans le sens vu ci-dessus mais aussi pour désigner un ensemble fini
- D'autres utilisent cette expression uniquement pour les ensembles satisfaisant la définition, et préfèrent employer l'expression ensemble au plus dénombrable pour désigner un ensemble soit fini, soit dénombrable.
Il faut donc prendre garde à la convention utilisée lors de la lecture d'une publication sur le sujet. Dans cet article, c'est la seconde acception qui sera utilisée.
Ensembles usuels et dénombrabilité
- Par définition, l'ensemble

- L'ensemble
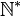
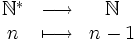
- L'ensemble des entiers naturels pairs, noté
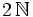
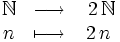
- L'ensemble des carrés parfaits, noté ici
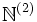
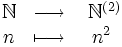
On doit à Galilée la remarque qu'il y a " autant " de carrés parfaits que d'entiers naturels, mettant ainsi en défaut l'affirmation classique (qu'on trouve dans les Éléments d'Euclide): " Le tout est plus grand que la partie. "
- L'ensemble

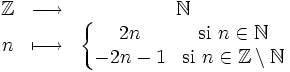
- L'ensemble
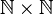
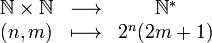
- L'ensemble

- L'ensemble
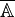


Quelques propriétés
Partie d'un ensemble dénombrable
- Toute partie A de

En effet, si A est fini, alors a fortiori A est au plus dénombrable.
Supposons maintenant A infini. Étant une partie non-vide de

Soit
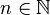
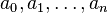
-
- (i)
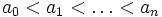
- (ii)
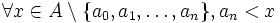
- (i)
L'ensemble
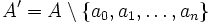
-
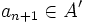
-
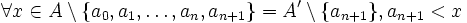
On a ainsi montré par récurrence l'existence d'une suite
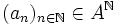
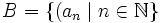
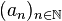
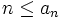
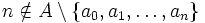
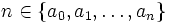
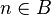
On a ainsi prouvé que A = B, et donc que A est dénombrable.
Dans tous les cas, A est donc au plus dénombrable.
- Toute partie d'un ensemble au plus dénombrable est au plus dénombrable.
Soit E un ensemble au plus dénombrable et F une partie de E. Soit



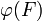

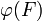
Produit d'ensembles dénombrables
Tout produit cartésien d'une famille finie d'ensembles dénombrables est dénombrable.
Soient A et B deux ensembles dénombrables. Il existe une bijection



Cette application est bijective de
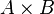
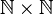
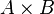
Une récurrence permet d'étendre ce résultat au produit cartésien de toute famille finie d'ensembles dénombrables.
Image et image réciproque d'ensembles dénombrables
Soient E et F deux ensembles non vides, et f une application de E dans F.
- 1. Si f est injective et si F est au plus dénombrable, alors E est au plus dénombrable.
f étant injective, elle induit une bijection de E sur f(E). Or, f(E) est une partie de F et est donc au plus dénombrable. E est donc au plus dénombrable.
- 2. Si f est surjective et si E est au plus dénombrable, alors F est au plus dénombrable.
E étant au plus dénombrable, il existe
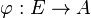
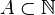

-
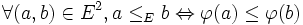
dès lors, toute partie non vide de E possède un minimum.
Soit
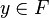
-
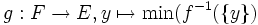
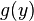
Par construction, pour tout
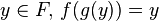
Corollaire : les trois propositions suivantes sont équivalentes :
- L'ensemble E est au plus dénombrable.
- Il existe une injection de E vers

- Il existe une surjection de

Réunion d'ensembles dénombrables
La réunion de toute famille dénombrable d'ensembles dénombrables est dénombrable
Plus formellement, si I est un ensemble dénombrable et si
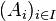
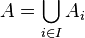


-
-
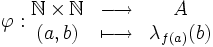
-

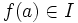
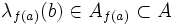
Montrons que

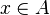
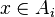
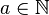
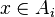

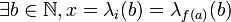
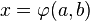
Ainsi,

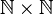
Toute réunion finie d'ensembles dénombrables est dénombrable
Dans le cas où I est fini, il suffit de reprendre la démonstration précédente, mais avec f surjective de

Toute réunion au plus dénombrable d'ensembles au plus dénombrables est au plus dénombrable
Dans le cas où certains Ai sont finis, il suffit de reprendre la démonstration précédente, mais avec λi surjective de

Dénombrabilité de l'ensemble des rationnels
On justifie ici, à l'aide de certaines des propriétés précédemment établies, la dénombrabilité de l'ensemble
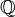
L'application
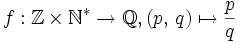
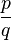
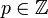
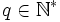
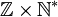
L'existence de cette surjection implique alors que
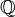
On peut aussi montrer que la suite
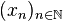

-
- x0 = 0
-
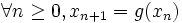
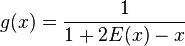
Voici les premières valeurs de la suite :