Algèbre nouvelle - Définition

L'Isagoge

Son nom exact est In artem analyticem Isagoge (1591) ; il est le programme déclaré de ce vaste projet axiomatique.

L'ouvrage, de 18 pages, disponible sur Gallica, est écrit en latin par François Viète. Il s'annonce comme le premier d'une série divisée en dix parties :

• In artem Analyticem Isagoge
• Ad Logiticem speciosam Nota priores
• Zeteticorum libri quinque
• De numerosa potestatum ad exegesim resolution
• De recognitione Aequationum
• Ad logiticem speciosam nota posteriores
• Effectionum geometricarum Canonica recensio
• Supplementum Geometria
• Analytica angularium sectionum in tres partes
• Varorium de rebus Mathematicis responsorum

Il fournit à lui seul une approche nouvelle de l'écriture algébrique et s'ouvre sur la fameuse dédicace à la princesse mélusinide Catherine de Parthenay dont on trouvera une traduction par Frédéric Ritter.

chapitre I : Présentation

Dans une première partie, Viète donne les définitions de son analyse spécieuse. Celle-ci se décompose dans un mouvement ternaire : Zététique, Poristique, Exégétique. Elle a pour but de fournir la Doctrine pour bien inventer en Mathématiques.

• La Zététique est la mise en équation du problème et la manipulation de cette équation pour la mettre sous une forme canonique qui donne lieu à une interprétation en termes de proportions.
• La Poristique est l'examen de la vérité des propositions au travers des théorèmes ordinaires.
• L'Exégétique, est la détermination, Vasset dira l'exhibition, des solutions, numériques ou géométriques, obtenues à partir des propositions générales de la poristique.

Il s'agit de la mise en place, concomitante, d'une axiomatique de calculs sur les grandeurs (connues et inconnues) et d'un programme, censé fournir des règles euristiques, qui impose trois étapes à la résolution d'un problème algébrique ou géométrique : la Formalisation, la Résolution générale, la Résolution particulière.

Viète y ajoute que, contrairement aux anciens analystes, sa méthode fait agir la résolution sur des symboles (non iam in numeris sed sub specie), ce qui en est un des apports majeurs. Il prédit en outre, qu'après lui, la formation à la Zététique se fera par l'analyse des symboles et non par celle des chiffres.

chapitre II De Symbolis aequalitum et proportionum

Viète continue, dans cette seconde partie, à décrire les symboles employés dans les égalités et les proportions ; il donne des règles axiomatiques :

• De 1 à 6 sur les propriétés de l'égalité :

La transitivité de l'égalité, sa conservation par somme, soustraction, produit, et division,

• de 7 à 11 sur les propriétés des lois sur les fractions.
• de 15 et 16 sur l'égalité de fractions.

chapitre III : De lege homogeneorum...

Viète poursuit ensuite en donnant les lois d'homogénéité ; distinguant ainsi les symboles selon leur puissances, 1 étant le côté (ou racine), 2 le carré, 3 le cube, etc. Cela exige que les facteur de ces puissances soient d'homogénéité complémentaire, qu'il note

1. Longueur, 2 Plane, 3 Solide, puis 4 Plane/Plane, 5 Plane/Solide, 6 Solide/Solide, etc comme s'il avait l'intuition qu'une géométrie puisse se déployer au-delà de l'ordinaire dimension 3.

chapitre IV De praeceptis logistices speciosae

Viète fournit dans ce quatrième chapitre les préceptes de la logique spécieuse, c'est-à-dire les axiomes d'addition, de produit, etc, de symboles désignant des grandeurs de natures comparables.

Dans un premier temps, son attention se porte sur l'addition des grandeurs de même ordre, leur soustraction, en donnant des règles comme A − (B + D) = A − B − D ou A − (B − D) = A − B + D

Puis, dans un second temps sur la dénomination des produits de quantités homogènes, sur la dénomination des quotients. Il note alors

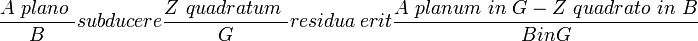
ce qu'on note aujourd'hui sans s'attacher à marquer l'homogénéité des facteurs.

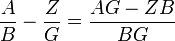
chapitre V : Des lois de la Zététique

Dans ce chapitre se trouve renfermés les fondements de la formulation des équations et particulièrement dans le point 5 de ce chapitre, l'idée qu'il convient de réserver certaines lettres aux quantités connues (datas) et d'autres aux quantités inconnues (incertitus), Viète désignant, dans une première version, les premières par des voyelles et les secondes par des consonnes.

Suivent alors quelques propositions.

L'ouvrage se termine sur deux courts chapitres qui décrivent comment en pratique, il convient de mener l'analyse du problème, sa résolution et sa vérification géométrique.

chapitre VI : Des théorèmes de l'examen poristique

Viète développe l'idée que, une fois la modélisation achevée par l'art de la zététique, le mathématicien produit ses théorèmes selon son invention et dans les règles de la syntaxe, comme cela a été établi depuis l'antiquité avec Apollonius, Théon et Archimède.

chapitre VII : De la Rhétique ou exégétique

Divisant l'exégétique en deux parts, une numéreuse et une géométrique, Viète explicite dans ce chapitre la nécessité de transformer la 'formule' générale obtenue à la fin de l'examen poristique en un résultat chiffré ou une construction géométrique. Le mathématicien doit, selon les cas, se faire arithméticien, en montrant qu'il sait extraire les racines et calculer leurs affectations ou géomètre et établir par une figure le résultat vrai. Il précise d'ailleurs que le résultat obtenu sur les lettres est également vrai, mais d'une vérité d'une autre nature qu'il ne précise pas.

chapitre VIII : Épilogue

Dans cette dernière partie, Viète définit encore quelques notations, et résume les vingt-neuf étapes du raisonnement ; il y définit notamment les racines d'ordre 1 et 2 (en fait carrée et cubique dans la nomenclature actuelle). À la fin de ce chapitre il annonce que, par cette méthode, on pourra résoudre le problème de tous les problèmes, à savoir : ne laisser aucune question irrésolue ou Non nullum probeblum solvere

Variantes de 1631

Le manuscrit publié par Vasset contient en place de la définition de la poristique et de l'exégétique, quelques résultats sur le développement du binôme (jusqu'au degré 6) et des théorèmes généraux de poristique dont la façon d'insérer tant de moyennes proportionnelles qu'on voudra entre deux longueurs.

Ce qui signifie que la suite A⁶,A⁵B,A⁴B²,A³B³,A²B⁴,AB⁵,B⁶ est géométrique.

Traduisant Viète, Vasset écrit :

A -B cubus cubus aequabitur A cubo-cubus - 6 A quadrato-cubus in B +15 A quad.quad. i n B quad. -20 A cubus in B cubum + 15A quadratum in B quad.-quad- 6 A B quad.-cub. + B cubus-cubus

en place de (A − B)⁶ = A⁶ − 6A⁵B + 15A⁴B² − 20A³b³ + 15A²B⁴ − 6AB⁵ + B⁶.

Il donne ensuite la règle de formation des coefficients binomiaux (déjà connue de Tartaglia et de Stiffel), notant que pour former les coefficients du développement, il suffit d'additionner, dans le développement de la puissance précédente, le premier et le second coefficient, le second et le troisième, etc. Ce qui donne en pratique le triangle de Pascal.