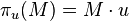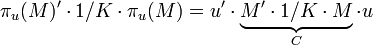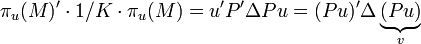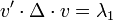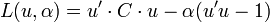Analyse en composantes principales - Définition

Exemples introductifs

Les deux axes d'une ACP sur la photo d'un poisson

Premier exemple

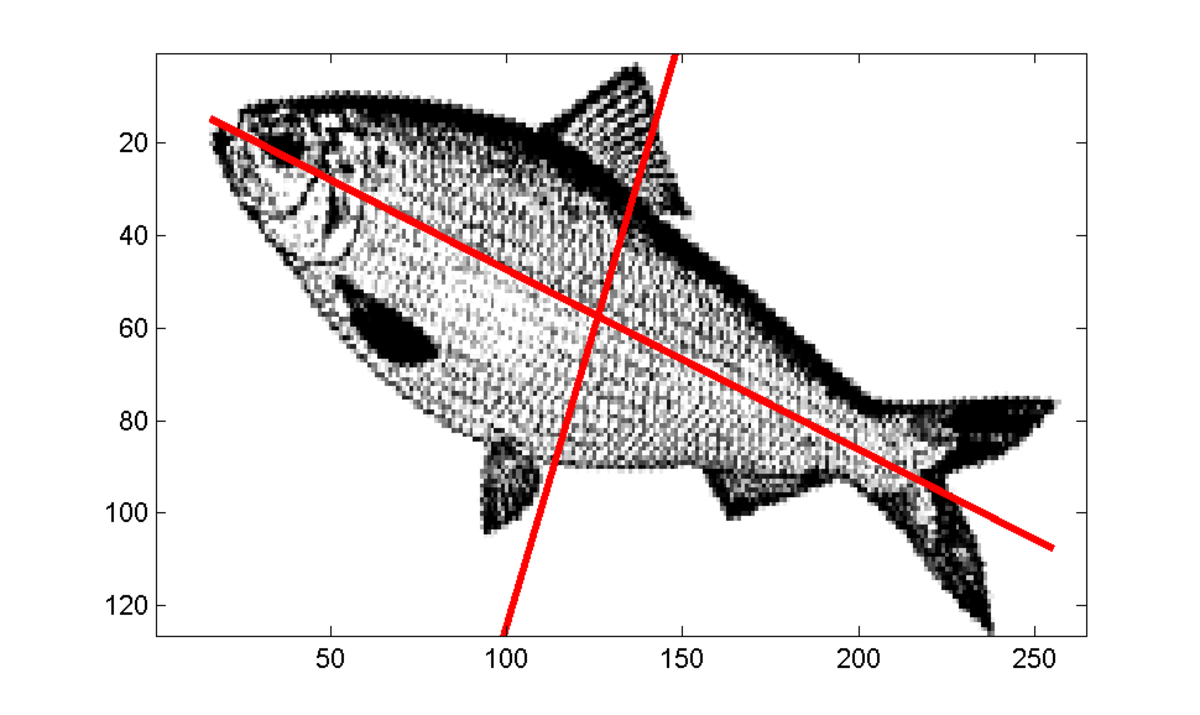
Dans le cas d'une image, comme dans la figure ci-contre, les pixels sont représentés dans un plan et considérés comme une variable aléatoire à deux dimensions. L'ACP va déterminer les deux axes qui expliquent le mieux la dispersion de l'objet, interprété comme un nuage de points. Elle va aussi les ordonner par inertie expliquée, le second axe étant perpendiculaire au premier.

Second exemple

Dans une école imaginaire, on n'enseigne que deux matières sur lesquelles les élèves sont notés: le français et les mathématiques. En appliquant l'ACP au tableau de notes, on dégagera probablement en premier axe des valeurs par élève très proches de leur moyenne générale dans les deux matières. C'est cet axe qui résumera au mieux la variabilité des résultats selon les élèves. Mais un professeur voulant pousser l'analyse des résultats, s'intéressa aussi au second axe, qui ordonne les élèves selon l'ampleur de leurs écarts entre les deux notes, et indépendamment du premier axe.

On comprend l'intérêt de la méthode d'ACP quand on étend l'analyse à 10 matières enseignées: la méthode va calculer pour chaque élève 10 nouvelles valeurs, selon 10 axes, chacun étant indépendant des autres. Les derniers axes apporteront très peu d'information au plan statistique: ils mettront probablement en évidence quelques élèves au profil singulier. Selon son point de vue d'analyse, le professeur veillera à ces élèves dans sa pratique quotidienne, corrigera peut-être une erreur qui s'est glissée dans son tableau, mais ne prendra pas en compte les derniers axes s'il s'agit d'une réflexion pédagogique plus globale.

La puissance de l'ACP est qu'elle sait aussi prendre en compte des données de nature hétérogène: par exemple un tableau des différents pays du monde avec le PNB par habitant, le taux d'alphabétisation, le taux d'équipement en téléphones portables, le prix moyen du hamburger, etc... Elle permet d'avoir une intuition rapide des effets conjoints entre ces variables.

Résultats théoriques

Si les sections précédentes ont travaillé sur un échantillon issu de la loi conjointe suivie par X₁, …, X_N, que dire de la validité de nos conclusions sur n'importe quel autre échantillon issu de la même loi ?

Plusieurs résultats théoriques permettent de répondre au moins partiellement à cette question, essentiellement en se positionnant par rapport à une distribution gaussienne comme référence.

Critère d'inertie

Dans la suite de cet article, nous considèrerons que le nuage est transformé (centré et réduit si besoin est). Chaque X_n est donc remplacé par ou . Nous utiliserons donc la matrice M pour noter ou suivant le cas.

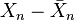
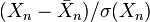
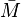
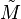
Le principe de l'ACP est de trouver un axe u, issu d'une combinaison linéaire des X_n, tel que la variance du nuage autour de cet axe soit maximale.

Pour bien comprendre, imaginons que la variance de u soit égale à la variance du nuage; on aurait alors trouvé une combinaison des X_n qui contient toute la diversité du nuage original (en tout cas toute la part de sa diversité captée par la variance).

Un critère couramment utilisé est la variance de l'échantillon (on veut maximiser la variance expliquée par le vecteur u). Pour les physiciens, cela a plutôt le sens de maximiser l'inertie expliquée par u (c'est-à-dire minimiser l'inertie du nuage autour de u).

Projection

Finalement, nous cherchons le vecteur u tel que la projection du nuage sur u ait une variance maximale. La projection de l'échantillon des X sur u s'écrit :

la variance empirique de π_u(M) vaut donc :

où C est la matrice de covariance.

Comme nous avons vu plus haut que C est diagonalisable dans une base orthonormée, notons P le changement de base associé et Δ la matrice diagonale formée de son spectre :

Après cette réécriture, nous cherchons le vecteur unitaire v qui maximise v'Δv, où Δ = Diag(λ₁, …, λ_N) est diagonale (rangeons les valeurs de la diagonale de Δ en ordre décroissant). On peut rapidement vérifier qu'il suffit de prendre le premier vecteur unitaire ; on a alors :

Plus formellement, on démontre ce résultat en maximisant la variance empirique des données projetées sur u sous la contrainte que u soit de norme 1 (par un Multiplicateur de Lagrange α) :

On obtient ainsi les deux résultats suivants:

1. u est vecteur propre de C associé à la valeur propre λ₁
2. u est de norme 1

La valeur propre λ₁ est la variance empirique sur le premier axe de l'ACP.

On continue la recherche du deuxième axe de projection w sur le même principe en imposant qu'il soit orthogonal à u.

Diagonalisation

La diagonalisation de la matrice de corrélation (ou de covariance si on se place dans un modèle non réduit), nous a permis d'écrire que le vecteur qui explique le plus d'inertie du nuage est le premier vecteur propre. De même le deuxième vecteur qui explique la plus grande part de l'inertie restante est le deuxième vecteur propre, etc.

Nous avons vu en outre que la variance expliquée par le k-ième vecteur propre vaut λ_k.

Finalement, la question de l'ACP se ramène à un problème de diagonalisation de la matrice de corrélation.

Numériquement

Numériquement, la matrice M étant rectangulaire, il est plus économique de la décomposer en valeurs singulières, puis de recombiner la décomposition obtenue, plutôt que de diagonaliser M' M.