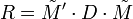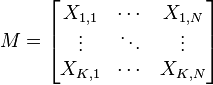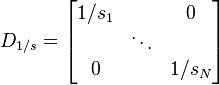Analyse en composantes principales - Définition

Introduction

L'Analyse en Composantes Principales (ACP) est une méthode de la famille de l'analyse des données et plus généralement de la statistique multivariée, qui consiste à transformer des variables liées entre elles (dites "corrélées" en statistique) en nouvelles variables indépendantes les unes des autres (donc "non corrélées"). Ces nouvelles variables sont nommées "composantes principales", ou axes. Elle permet au praticien de réduire l'information en un nombre de composantes plus limité que le nombre initial de variables.

Il s'agit d'une approche à la fois géométrique (représentation des variables dans un nouvel espace géométrique selon des directions d'inertie maximale) et statistique (recherche d'axes indépendants expliquant au mieux la variabilité - la variance - des données). Lorsqu'on veut alors compresser un ensemble de N variables aléatoires, les n premiers axes de l'ACP sont un meilleur choix, du point de vue de l'inertie ou la variance expliquée (cf plus loin).

Histoire

Extrait de l'article de Pearson de 1901: la recherche de la "droite du meilleur ajustement"

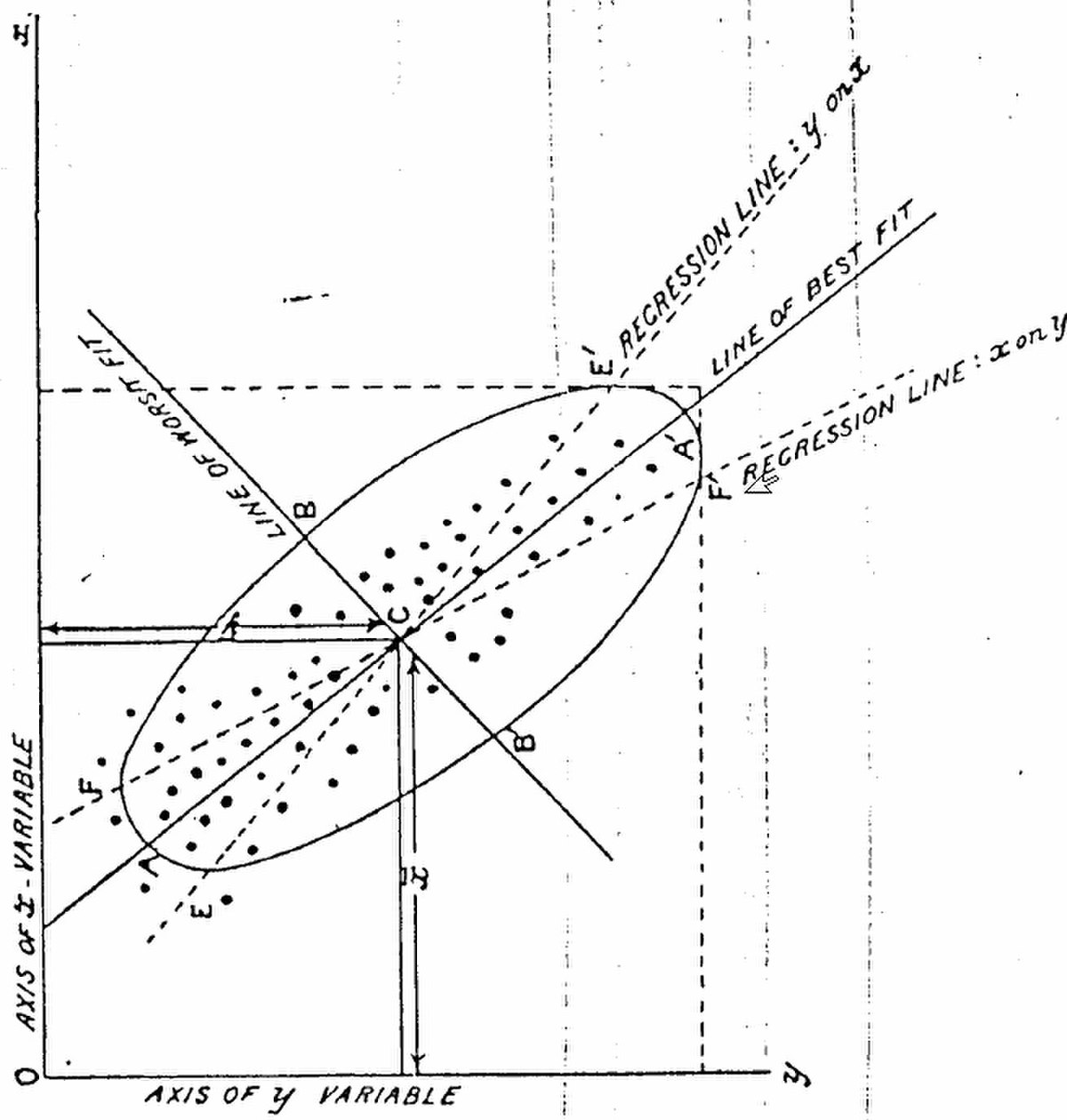
L'ACP prend sa source dans un article de Karl Pearson publié en 1901. Le père du Test du χ² y prolonge ses travaux dans le domaine de la régression et des corrélations entre plusieurs variables. Pearson utilise ces corrélations non plus pour expliquer une variable à partir des autres (comme en régression), mais pour décrire et résumer l'information contenue dans ces variables.

Encore connue sous le nom de transformée de Karhunen-Loève ou de transformée de Hotelling, l'ACP a été de nouveau développée et formalisée dans les années 30 par Harold Hotelling . La puissance mathématique de l'économiste et statisticien américain le conduira aussi à développer l'analyse canonique, généralisation des analyses factorielles dont fait partie l'ACP.

Les champs d'application sont aujourd'hui multiples, allant de la biologie à la recherche économique et sociale, et plus récemment le traitement d'images. L'ACP est majoritairement utilisée pour:

• décrire et visualiser des données ;
• les décorréler ; dans la nouvelle base, constituée des nouveaux axes, les variables ont une corrélation nulle ;
• les débruiter, en considérant que les axes que l'on décide d'oublier sont des axes bruités.

Échantillon

On applique usuellement une ACP sur un ensemble de N variables aléatoires X₁, …, X_N connues à partir d'un échantillon de K réalisations conjointes de ces variables.

Cet échantillon de ces N variables aléatoires peut être structuré dans une matrice M à K lignes et N colonnes.

Chaque variable aléatoire X_n = (X_{1, n}, …, X_{K, n})' a une moyenne et un écart type σ_Xn.

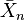
Poids

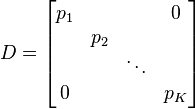
Si les réalisations (les éléments de la matrice M) sont à probabilités égales alors chaque réalisation (un élément X_i,j de la matrice) a la même importance 1 / n dans le calcul des caractéristiques de l'échantillon. On peut aussi appliquer un poids p_i différent à chaque réalisation conjointes des variables (cas des échantillons redressés, des données regroupées, ...). Ces poids, qui sont des nombres positifs de somme 1 sont représentés par une matrice diagonale D de taille K:

Dans le cas le plus usuel de poids égaux, où I est la matrice identité.

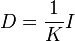
Transformations de l'échantillon

Le vecteur est le centre de gravité du nuage de points ; on le note souvent g. On a g = M'D1 où 1 désigne le vecteur de R^K dont toutes les composantes sont égales à 1.

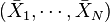
La matrice M est généralement centrée sur le centre de gravité :

.

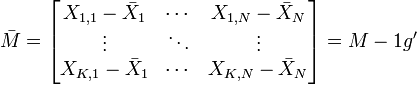
Elle peut être aussi réduite :

.

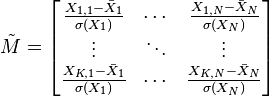
Le choix de réduire ou non le nuage de points (i.e. les K réalisations de la variable aléatoire (X₁, …, X_N)) est un choix de modèle :

• si on ne réduit pas le nuage : une variable à forte variance va « tirer » tout l'effet de l'ACP à elle ;
• si on réduit le nuage : une variable qui n'est qu'un bruit va se retrouver avec une variance apparente égale à une variable informative.

Calcul de covariances et de corrélations

Une fois la matrice M transformée en ou , il suffit de la multiplier par sa transposée pour obtenir:

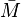
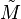
• la matrice de variance-covariance des X₁, …, X_N si M n'est pas réduite ;
• la matrice de corrélation des X₁, …, X_N si M est réduite.

Ces deux matrices sont carrées (de taille N), symétriques, et réelles. Elles sont donc diagonalisables dans une base orthonormée.

De façon plus générale, la matrice de variance-covariance s'écrit . Si l'on note D_{1 / s} la matrice diagonale des inverses des écarts-types:

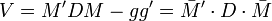
et la matrice diagonale des inverses des variances, alors on a:

.

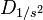
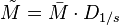
La matrice des coefficients de corrélation linéaire entre les N variables prises deux à deux, notée R, s'écrit:

.