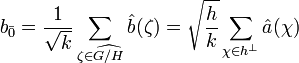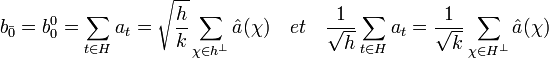Analyse harmonique sur un groupe abélien fini - Définition
La liste des auteurs de cet article est disponible ici.
Théorie de l'analyse harmonique
Transformée de Fourier
L'égalité de Parseval dans le cas d'un espace de dimension finie montre que tout élément a de C[G] vérifie l'égalité suivante :

Ici (as) désigne les coordonnées de a dans la base canonique et (aχ) les coordonnées de a dans la base des caractères.
-
- La transformée de Fourier d'un élément a de C[G] correspond à la fonction généralement notée
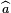
- La transformée de Fourier d'un élément a de C[G] correspond à la fonction généralement notée
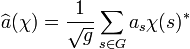
-
- La transformée de Fourier est une application linéaire de l'algèbre de G dans son dual.
Egalité de Parseval
Le produit hermitien génère une isométrie canonique entre l'algèbre de G et son dual. Il est donc possible de les identifier, dans ce contexte, la propriété suivante est vérifiée :
-
- La transformée de Fourier sur le groupe G est une isométrie linéaire de l'algèbre du groupe G dans l'algèbre de son dual ce qui se traduit par l'égalité suivante, dite de Parseval :
![\forall a, b \in \mathbb C[G] \quad <a|b>_{\mathbb C[G]} =<\hat a|\hat b>_{\mathbb C[\widehat G]}](https://upload.wikimedia.org/math/e/4/7/e4736958c8025e8629cc6ef4c162027f.png)
Si b est égal à a, alors comme le groupe dual est une base orthonormale de son algèbre :
![<\hat a|\hat a>_{\mathbb C[\widehat G]}=\frac 1g \sum_{\chi \in \widehat G} \hat a (\chi)^*.\hat a (\chi)= \frac {1}{g^2} \sum_{\chi \in \widehat G} \sum_{s,t \in G} a_s^*\chi(s).a_t\chi(t)^* = \frac {1}{g^2} \sum_{\chi \in \widehat G} \sum_{s \in G} |a_s|^2 = \frac 1g \sum_{s \in G} |a_s|^2 = <a|a>_{\mathbb C[G]} \;](https://upload.wikimedia.org/math/5/6/f/56f73375048e1fc61611d37e583e0de7.png)
Enfin, dans le cas général :


On en déduit :

Le même calcul sur <a + b , i(a + b)> montre que les parties imaginaires sont aussi égales. Ce qui démontre le caractère isométrique de la transformation.
L'aspect injectif de la transformation provient du fait qu'elle est une isométrie, la surjectivité se se démontre en remarquant que les deux espaces de départ et d'arrivée ont même dimension.Formule de Plancherel
-
- La formule suivante, dite d'inversion de Plancherel, est vérifiée.
![\forall a \in \mathbb C[G] \quad a = \frac 1{\sqrt g} \sum_{\chi \in \widehat G} \widehat a(\chi) \chi \;](https://static.techno-science.net/illustration/Definitions/autres/2/26b517872b05ee078db56ec87061d388_681c1aae157057bb3b638d00b62284c7.png)
En effet, les produits hermitiens de chacun des deux membres de l'égalité par un même caractère sont égaux :

Produit de convolution
Le produit de convolution se définit simplement dans ce contexte :
-
- Soit a et b deux éléments de l'algèbre du groupe G ayant pour coordonnées (as) et (bs), le produit de convolution de a et de b, noté a * b, est l'élément de l'algèbre ayant les coordonnées (cs) définies par :
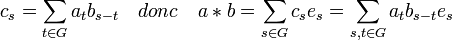
On dispose de la proposition suivante :
-
- Soit a et b deux éléments de l'algèbre du groupe G, la transformée de Fourier de a * b est le produit des transformées de Fourier de a et de b.
![\forall a,b \in \mathbb C[G] \quad \widehat {a*b} \,(\chi) = \hat a (\chi).\hat b (\chi)\;](https://static.techno-science.net/illustration/Definitions/autres/b/be7c9a4a4411096f7e8aee1f2f3d2bd7_b838f4b1d60af952917535c411322e52.png)
En effet, si χ est un caractère du groupe :
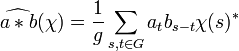
Si l'on note u la valeur s - t, on obtient :
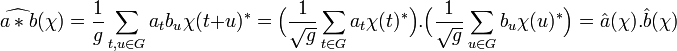
On en déduit les propriétés usuelles du produit de convolution :
-
- Le produit de convolution est une opération interne de l'algèbre du groupe commutative, associative, distributive par rapport à l'addition.
On peut exprimer ces propriétés de la manière suivante :
-
- La structure (C[G], + , *) est une algèbre semi-simple isomorphe à l'algèbre du dual de G et donc à C[G].
En effet, il suffit de remarquer que G et son dual sont isomorphes.
Dualité de Pontryagin
-
- Soit H un sous-groupe de G, on appelle groupe orthogonal de H, souvent noté
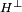
- Soit H un sous-groupe de G, on appelle groupe orthogonal de H, souvent noté
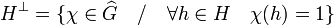
La dualité de Pontryagin s'exprime à travers les trois propriétés suivantes :
-
- G et son bidual sont canoniquement isomorphes.
- Le dual du quotient G/H est isomorphe à l'orthogonal de H.
- Le dual de H est isomorphe au quotient du dual de G par l'orthogonal de H.
-
- G et son bidual sont canoniquement isomorphes.
La démonstration est donnée dans le paragraphe Bidual de l'article caractère d'un groupe fini.
-
- Le dual du quotient G/H est isomorphe à l'orthogonal de H.
Soit S la surjection canonique de G dans G/H, considérons l'application φ du dual de G/H dans le dual de G définie par :
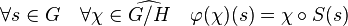
Si χ est un caractère de G/H, alors φ(χ) est la composée de deux morphismes donc est un morphisme et il est à valeur dans C*, φ(χ) est donc un caractère de G. On remarque de plus que φ est clairement un morphisme de groupe.
Le noyau de S est égal à H, φ possède donc une image incluse dans l'orthogonal de H. Montrons alors que tout élément ζ de l'orthogonal de H possède un antécédent par φ. On remarque que ζ est constant sur toutes les classes de G/H, en effet :
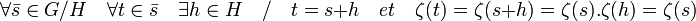
Soit χ le caractère du groupe G/H défini par :
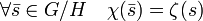
La fonction χ est bien définie car ζ est constant sur toutes les classes de G/H, elle définit bien un morphisme et χ est un caractère de G/H. Son image par φ est clairement égal à ζ. L'application φ possède donc pour image l'orthogonal de H. Son noyau est composé du caractère constant égal à un sur toutes les classes de G/H et l'application φ est donc injective, elle est donc un isomorphisme entre le dual de G/H et le groupe orthogonal de H, ce qui termine la démonstration.
-
- Le dual de H est isomorphe au quotient du dual de G par l'orthogonal de H.
Soit ψ l'application du dual de G dans le dual de H qui à un caractère du groupe G associe sa restriction à H. L'application ψ est un morphisme de groupe.
Son noyau est composé des caractères constants égaux à 1 sur H, c'est-à-dire à l'orthogonal de H. Par passage au quotient, on obtient un morphisme θ du quotient du dual de G par l'orthogonal de H à valeur dans le dual de H. La proposition précédente montre l'égalité entre les ordres des ensembles de départ et d'arrivée de θ, et comme θ est injective, la proposition est démontrée.Formule sommatoire de Poisson
Dans ce paragraphe H désigne un sous-groupe de G, h son ordre et k l'ordre du groupe orthogonal de H. L'égalité h.k = g est donc vérifiée. On note a un élément de l'algèbre de G et as ses coordonnées dans la base canonique.
-
- L'égalité suivante, dite formule sommatoire de Poisson est vérifiée :
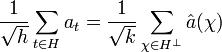
Soit b0 l'élément de l'algèbre de coordonnées (bs0) dans la base canonique de C[G] définies par les égalités suivantes :
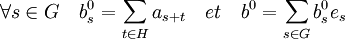
Les coordonnées de b0 sont constante sur chaque classe de G/H, ce qui permet de définir un élément b de l'algèbre du groupe G/H dont les coordonnées dans la base canonique indexée par les éléments de G/H sont :
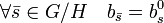
Appliquons alors la formule de Plancherel à l'élément b au point de coordonnées l'élément nul de G/H :
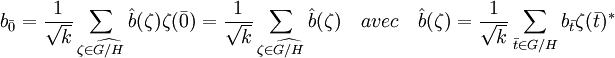
La dualité de Pontryagin montre qu'il existe un unique caractère χ de G tel que si t est un élément de
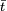
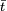
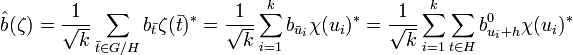
De plus, le caractère χ est constant sur chaque classe de G/H, on en déduit :
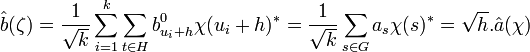
La dualité de Pontryagin indique que si ζ décrit les caractères de G/H, alors χ décrit le groupe orthogonal de H, on en déduit :