André Weil - Définition
La liste des auteurs de cet article est disponible ici.
Travaux
Il laisse des contributions remarquables dans nombre de domaines, et en premier lieu en géométrie algébrique et en théorie des nombres. Son travail doctoral conduisit au théorème de Mordell-Weil. Il formula l'argument de descente infinie, et pour ce faire, il définit une mesure de la taille des points rationnels d'une variété algébrique ; et il initia la cohomologie galoisienne, qui ne fut appelée ainsi que deux décennies plus tard. Ces deux aspects ont largement été développés depuis pour devenir des objets centraux de la géométrie algébrique actuelle.
Parmi ses plus grands travaux figure la preuve donnée en 1940, en prison, de l'hypothèse de Riemann pour les fonctions zêta des courbes sur les corps finis. Les conjectures de Weil ont largement influencé les géomètres algébristes depuis 1950 ; elles furent prouvées par Bernard Dwork, Alexandre Grothendieck (qui, pour les attaquer, mit sur pied un gigantesque programme visant à transférer les techniques de topologie algébrique en théorie des nombres), Michael Artin et enfin Pierre Deligne qui démontra, en 1973, l'hypothèse de Riemann sur les corps finis, partie la plus profonde des conjectures de Weil.
Dans les années 1930, il fournit une preuve du théorème de Riemann-Roch, à la suite des travaux de Claude Chevalley.
En topologie générale, il introduit le concept d'espace uniforme. Son travail sur les faisceaux fut très peu publié, mais apparut dans ses correspondances avec Henri Cartan à la fin des années 1940.
Plus basiquement, il a introduit la notation
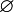
Distinctions
Il a reçu de nombreuses distinctions académiques dont le Prix Wolf de Mathématiques en 1979 et le Prix de Kyōto en 1994. Il a été membre honoraire de la London Mathematical Society, élu à l'académie des sciences de Paris et à la National Academy of Sciences aux États-Unis.
À sa mort, le seul honneur mentionné dans sa biographie officielle indiquait simplement « Membre, Académie des Sciences et des Lettres de Poldévie », un pays imaginaire où aurait enseigné le tout aussi imaginaire mathématicien Nicolas Bourbaki.
Bibliographie
- Sylvie Weil, Chez les Weil, Buchet-Chastel, Paris, 2009.

















































