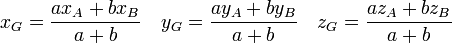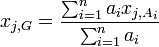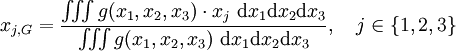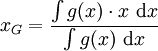Barycentre (physique) - Définition

Développement mathématique

Les mathématiques généralisent la construction d'Archimède du point d'équilibre de deux points affectés de deux masses positives progressivement à des ensembles plus complexes. Les coefficients peuvent être négatifs : Le barycentre des points A et B affectés des masses a et b (a + b non nul) est l'unique point G tel que

.

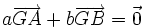
Les coordonnées de G sont alors

Le nombre de points peut passer à trois points, quatre points et se généraliser à n points. Si la somme des masses a_i est non nulle, le barycentre du système est le point G tel que

.

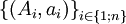
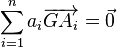
Les coordonnées sont données par les formules, pour j variant de 1 à la dimension de l'espace

C'est sous cette forme qu'il devient un outil puissant en géométrie affine.

Le nombre de points peut même devenir infini, permettant de trouver le barycentre d'une courbe ou d'une surface.

Si l'ensemble constitue un domaine D continu, à chaque point M du domaine on affecte une densité g(M) où g est une fonction continue (un champ scalaire). Le barycentre est alors le point G tel que

dans l'espace ou dans le plan .

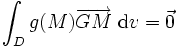
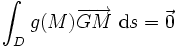
Si les points M ont pour coordonnées (x₁;x₂,x₃) la fonction de densité s'écrit g(x₁,x₂,x₃) et les coordonnées de G s'écrivent

Si l'on se ramène à une dimension, ou bien si l'on considère chaque coordonnée séparément, on retrouve la formule de la moyenne pondérée :

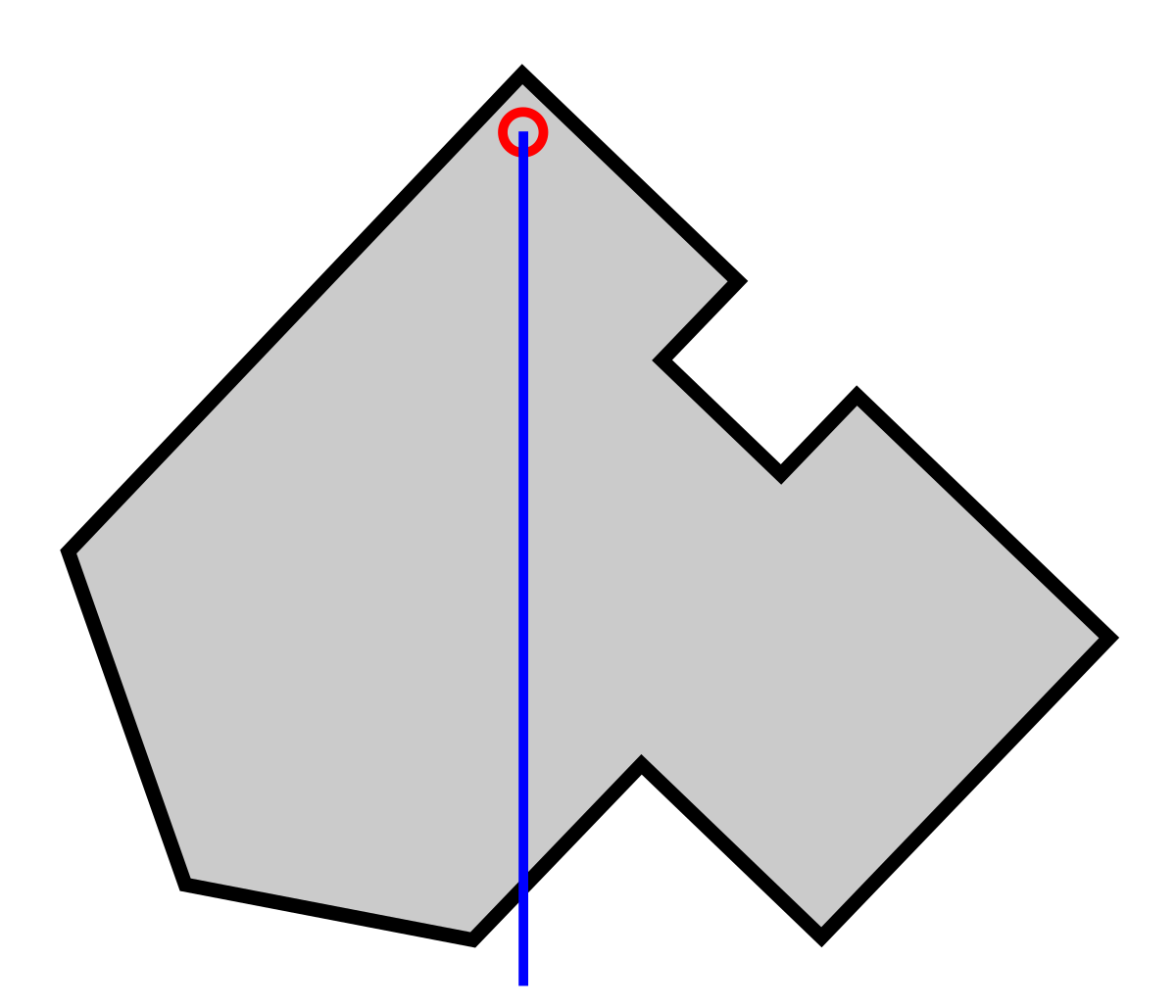
Localisation du centre de gravité d'une plaque à deux dimensions

Cette méthode est utile lorsque l'on souhaite trouver le centre de gravité d'un objet plan dont la forme est complexe et dont on ne connaît pas les dimensions exactes.

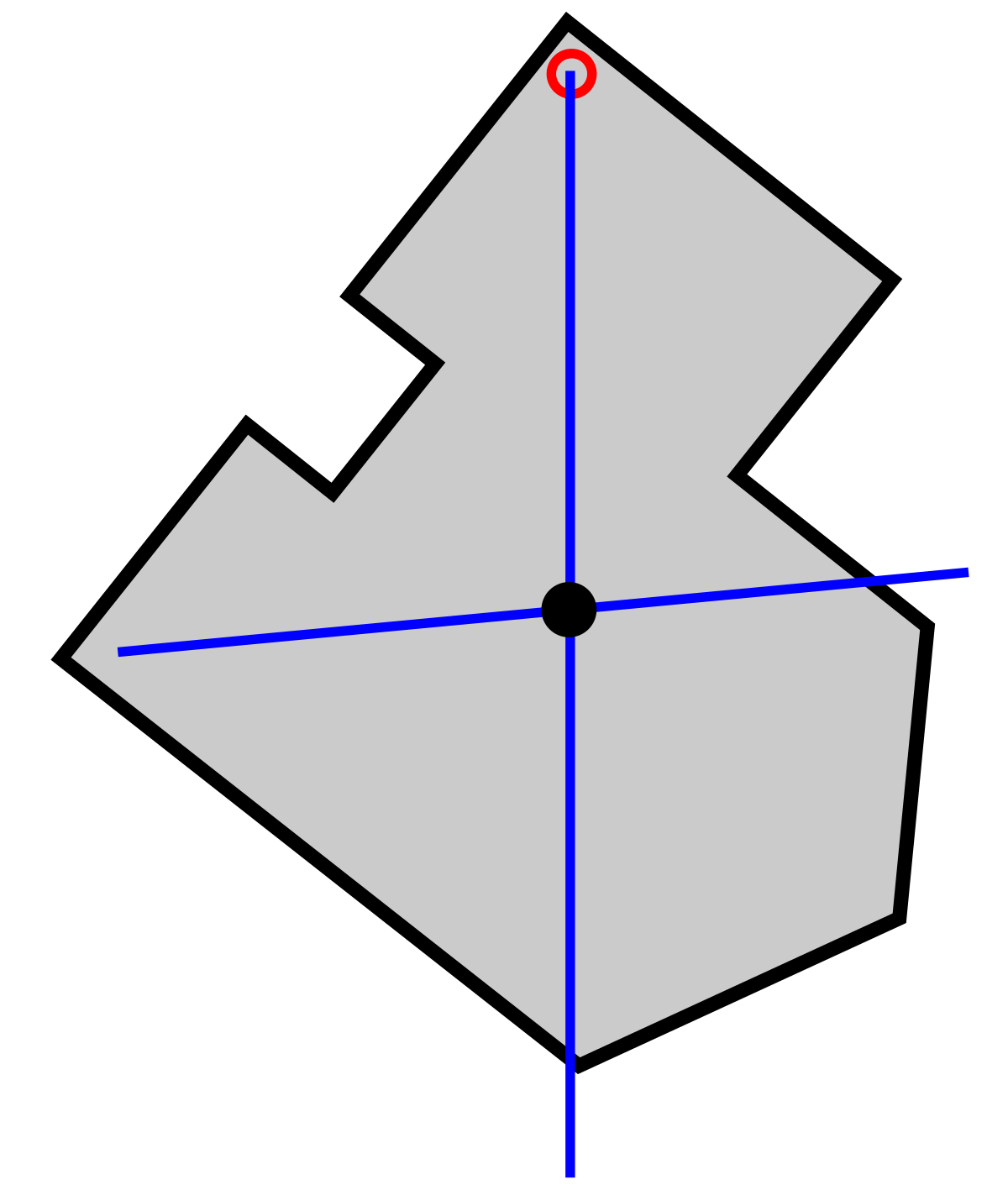
Étape 1: Une plaque de forme arbitraire.	Étape 2: Suspendre la plaque en un point proche d'un sommet et attendre la position d'équilibre. À l'aide d'un fil à plomb, tracer la verticale passant par ce point.	Étape 3: Suspendre la plaque en un autre point et tracer une seconde verticale. Le centre de gravité est à l'intersection des deux droites.

Astronomie

Animation impliquant 2 corps de faible différence de masse. Le barycentre se trouve à l'extérieur du corps principal comme dans le cas du couple Pluton/Charon.

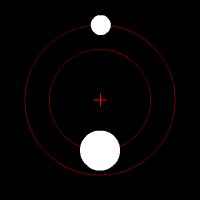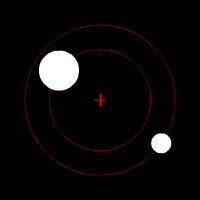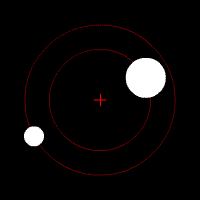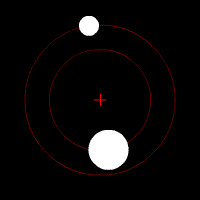
On parle de barycentre en ce qui concerne le couple formé par un corps stellaire possédant un satellite. Le barycentre est le point autour duquel l'objet secondaire gravite. Si la plupart des couples connus possède leur barycentre à l'intérieur de l'objet principal, il existe des exceptions notables :

• Le cas du couple Pluton/Charon : la différence de masse entre ces deux corps est relativement faible, le barycentre se trouve donc à l'extérieur de Pluton. Pour certains astronomes, plutôt que de parler de planètes et de satellites, il conviendrait dans ce cas précis de retenir la notion de « planète double ».
• Plusieurs astéroïdes reproduisent le cas de figure ci-dessus.
• Le barycentre du couple Jupiter/Soleil se trouve à l'extérieur de ce dernier à environ un rayon solaire de distance.
• On retrouve aussi cette particularité chez certaines étoiles doubles