Brisure spontanée de symétrie - Définition

Exemples

Dans les systèmes magnétiques (ferromagnétiques, antiferromagnétiques, ferrimagnétiques), la symétrie de rotation SO(3) des moments magnétiques et l'invariance par renversement du temps sont brisées spontanément.

Dans les cristaux liquides nématiques, l'invariance par rotation SO(3) est également en une symétrie de rotation autour d'un axe appelé directeur. Si est un vecteur unitaire parallèle à cet axe, la transformation de en ne change évidemment pas la direction de cet axe, et on peut donc choisir indifféremment n ou − n pour décrire le même état nématique. Cela constitue une différence importante avec le magnétisme où le changement du signe de l'aimantation ne redonne pas l'état thermodynamique initial.

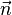
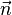
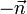
Dans les cristaux liquides smectiques A, les molécules s'organisent en couches séparées par une distance déterminées. Toutefois, à l'intérieur des couches, les molécules n'ont pas d'ordre à longue distance. Dans cet exemple, la symétrie de translation est brisée uniquement dans la direction perpendiculaire aux couches, et la symétrie de rotation est réduites aux rotations autour d'un axe orthogonal aux couches.

Dans les alliages métalliques cristallins, on peut observer des états ordonnés où l'un des atomes formant l'alliage occupe préférentiellement un site du réseau. Il en résulte un abaissement de la symétrie par rapport à celle de l'état à haute température dans lequel le site pouvait être occupé par un atome de l'une ou l'autre espèce. Dans ce cas, la brisure de symétrie réduit un groupe de translation discret à un sous groupe, alors que dans les exemples précédents la symétrie était brisée dans un groupe continu.

La symétrie brisée n'est pas toujours associée à des transformations géométriques. Par exemple, dans les supraconducteurs et dans les superfluides, la symétrie brisée est une symétrie de jauge continue abelienne U(1). C'est également le cas des brisures de symétries étudiées en physique des hautes énergies qui correspondent à des brisures de symétries pour des groupes non abeliens.

Théorème de Mermin-Wagner-Hohenberg-Coleman

En 1966, N. D. Mermin et H. Wagner ont établi un théorème montrant qu'une brisure spontanée d'une symétrie continue était impossible dans un système bidimensionnel. Une démonstration de ce théorème, utilisant uniquement l'inégalité de Bogoliubov peut être trouvée dans le livre de C. Itzykson et J. M. Drouffe. En 1967, P. C. Hohenberg a étendu ce théorème aux superfluides et aux supraconducteurs. Ce théorème a été reformulé par Sidney Coleman en 1973 dans le cadre de la théorie quantique des champs qui a montré que la théorie des champs hypothétique qui décrirait les bosons de Goldstone dans le cas d'une brisure spontanée de symétrie en dimension (1+1) ne pouvait pas satisfaire les axiomes de Wightman. Le théorème de Mermin-Wagner-Hohenberg-Coleman a comme conséquence que les modèles O(N) avec N > 1 en deux dimensions ne peuvent pas présenter d'ordre à longue distance.

Dans le cas N = 2, on a le modèle XY qui possède la transition de Berezinskii-Kosterlitz-Thouless, entre un désordre complet à haute température et un quasi-ordre à longue distance à basse température. Pour , le modèle O(N) est dans une phase désordonnée à toute température. Dans sa version théorie des champs, le théorème de Mermin-Wagner-Hohenberg-Coleman permet d'affirmer qu'une chaine de spins antiferromagnétique ne peut pas posséder un état de Néel même au zéro absolu.