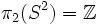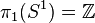Brisure spontanée de symétrie - Définition

Introduction

En physique, le terme brisure spontanée de symétrie renvoie au fait que, sous certaines conditions, certaines propriétés de la matière ne respectent pas les équations décrivant le mouvement des particules. Cette notion joue un rôle important en physique des particules et en physique de la matière condensée.

Définition

À haute température (ou à haute énergie), la matière forme un gaz ou un plasma et cet état possède toutes les symétries des équations décrivant le mouvement des particules. À basse température, la matière peut se trouver dans un état qui ne possède pas toutes les symétries des équations microscopiques, mais seulement un sous-groupe du groupe de symétrie complet. Ce phénomène est appelé brisure spontanée de symétrie. Un exemple concret d'état de la matière possédant une brisure spontanée de symétrie est l'état solide cristallin. Un cristal n'est en effet invariant que sous l'action d'un groupe de symétrie discret comprenant des translations discrètes, des réflexions et des rotations de 60°, 90°, 120°, 180° autour de plan ou d'axes particuliers, alors que l'équation de Schrödinger qui décrit le mouvement des électrons et des noyaux qui constituent ce cristal est invariante sous n'importe quelle translation, rotation ou réflexion.

Il existe en physique de la matière condensée de nombreux autres exemples de brisures spontanées de symétries.

Conséquences physiques des brisures de symétries

Lorsqu'une symétrie est brisée spontanément dans un système physique, il existe un nouveau paramètre qui est invariant sous l'action du sous-groupe laissant invariant l'état à symétrie brisée. Ce nouveau paramètre n'est en revanche pas invariant sous l'action du groupe complet laissant invariantes les équations du mouvement microscopiques. Ce paramètre est appelé le paramètre d'ordre et il mesure l'importance de la brisure de symétrie. L'orbite de ce paramètre d'ordre, sous l'action du groupe complet de symétrie, donne l'ensemble des états, physiquement non équivalents, dans lesquels la symétrie est brisée. Pour donner un exemple concret, dans le cas du magnétisme, le paramètre d'ordre est le vecteur aimantation, et l'orbite du paramètre d'ordre sous l'action du groupe de symétrie est la sphère S². L'existence d'un paramètre d'ordre est à la base de la théorie de Landau des transitions de phase. Dans un état à symétrie brisée, il existe des forces qui tendent à imposer une valeur uniforme du paramètre d'ordre dans tout le système. Ce phénomène est appelé rigidité généralisée. L'exemple le plus banal est l'existence d'un module de cisaillement dans un solide en plus du module de compression. Dans le cas d'un supraconducteur, c'est l'existence d'une rigidité généralisée qui permet d'expliquer la circulation d'un courant sans dissipation. La rigidité généralisée du supraconducteur combinée à l'invariance de jauge électromagnétique est également responsable de l'effet Meissner, comme l'a discuté P. W. Anderson. En physique des particules, un phénomène analogue, le phénomène de Higgs, permet d'expliquer la formation d'une masse pour les particules de jauge.

La description des états d'un système possédant une brisure de symétrie en termes d'un paramètre d'ordre permet également de classifier les défauts qui peuvent apparaitre dans un système au moyen des méthodes de la topologie algébrique. En effet, un état où le paramètre d'ordre varie dans l'espace peut être décrit au moyen d'une application de dans l'espace quotient du paramètre d'ordre. Par exemple, un état inhomogène d'un système magnétique peut etre représenté comme une application de dans la sphère S², et un état inhomogène d'un supraconducteur comme une application de dans la sphère S¹. Il peut exister des défauts stables du paramètre d'ordre seulement si l'application ne peut pas etre déformée continument en une application constante. De façon plus précise, la théorie de l'homotopie permet d'affirmer que si le groupe π₀ est non trivial, les défauts de type paroi sont stables, si le groupe π₁ est stable les défauts de type ligne sont stables, et si le groupe π₂ est non-trivial, les défauts de type point sont stables. En particulier, comme , un système magnétique peut présenter des défauts de type point, mais comme π₁(S²) = 0, il ne peut pas posséder de défauts de type ligne. Dans le cas du supraconducteur, , donc les lignes sont des défauts topologiquement stables. Ces défauts correspondent bien évidemment aux vortex. La théorie topologique permet également de prédire que ces vortex ont une charge quantifiée.