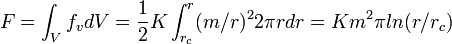Nématique - Définition

Introduction

Texture dans une phase nématique.

.

L'état nématique est un état de la matière intermédiaire entre les phases solide cristalline et liquide. Les molécules, de forme allongée, sont réparties sans ordre de position (comme dans un liquide) mais en demeurant en moyenne parallèles les unes aux autres, c'est-à-dire avec un ordre d'orientation à longue portée (comme dans un cristal).

Généralités

Orientation moyenne des molécules et directeur n.

Les molécules composant le nématique ont une forme cylindrique, la plupart des propriétés caractéristiques des nématiques en découle. Ainsi, le fluide nématique diffère du liquide isotrope par l'alignement spontané des molécules. La phase nématique naît de cet ordre d'orientation des molécules à grande distance, c'est un comportement collectif. L'orientation moyenne des molécules est appelée le directeur et est définie à π près.

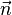
La substance est biréfringente, optiquement uniaxe positif. L'observation d'un échantillon au microscope montre des fils à l'intérieur. En référence à ces défauts, observés dans les fluides cristallins de O. Lehman, G. Friedel nomma cette phase « nématique » (du grec νεμα « fil »). Ce terme lui fut inspiré par sa fille Marie, bonne hélléniste, lors d'une après-midi de détente.

Si la viscosité de la phase nématique est du même ordre de grandeur que celle de la phase liquide isotrope, une forte anisotropie existe, la substance coule plus facilement lorsque l'écoulement est dans le sens du directeur que lorsqu'il est dans un plan perpendiculaire. Dans ce dernier cas, l'écoulement peut tendre à modifier l'orientation du directeur. L'étude de l'écoulement d'un nématique sous contrainte est appelée nématodynamique.

Le diagramme de phase classique est modifié, la phase nématique s'intercalant entre la phase liquide et la phase solide (ou/et une phase smectique le cas échéant), certaines substances possédant un point triple liquide-nématique-solide et d'autres susceptibles d'accepter la phase nématique pour une pression nulle.

Disinclinaisons

Les fils observés au microscope dans les nématiques sont des lignes de dislocation dans le fluide. Pour comprendre les disinclinaisons, il est possible d'utiliser l'approximation d'élasticité isotrope, on pose alors K₁₁ = K₂₂ = K₃₃ = K.

L'expression de l'énergie libre se simplifie et devient :

Disposition des molécules dans le cas m=-1/2

.

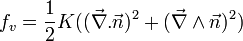
On considère une ligne de disinclinaison le long de l'axe z, le directeur étant contraint dans le plan (x,y), il fait un angle θ(x,y) avec l'axe x. Dans ce référentiel, le directeur a pour coordonnées (cos(θ), sin(θ),0).

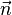
L'expression se calcule alors en fonction de θ :

.

Disposition des molécules dans le cas m=1/2

Cette énergie libre est minimale lorsque Δθ = 0.

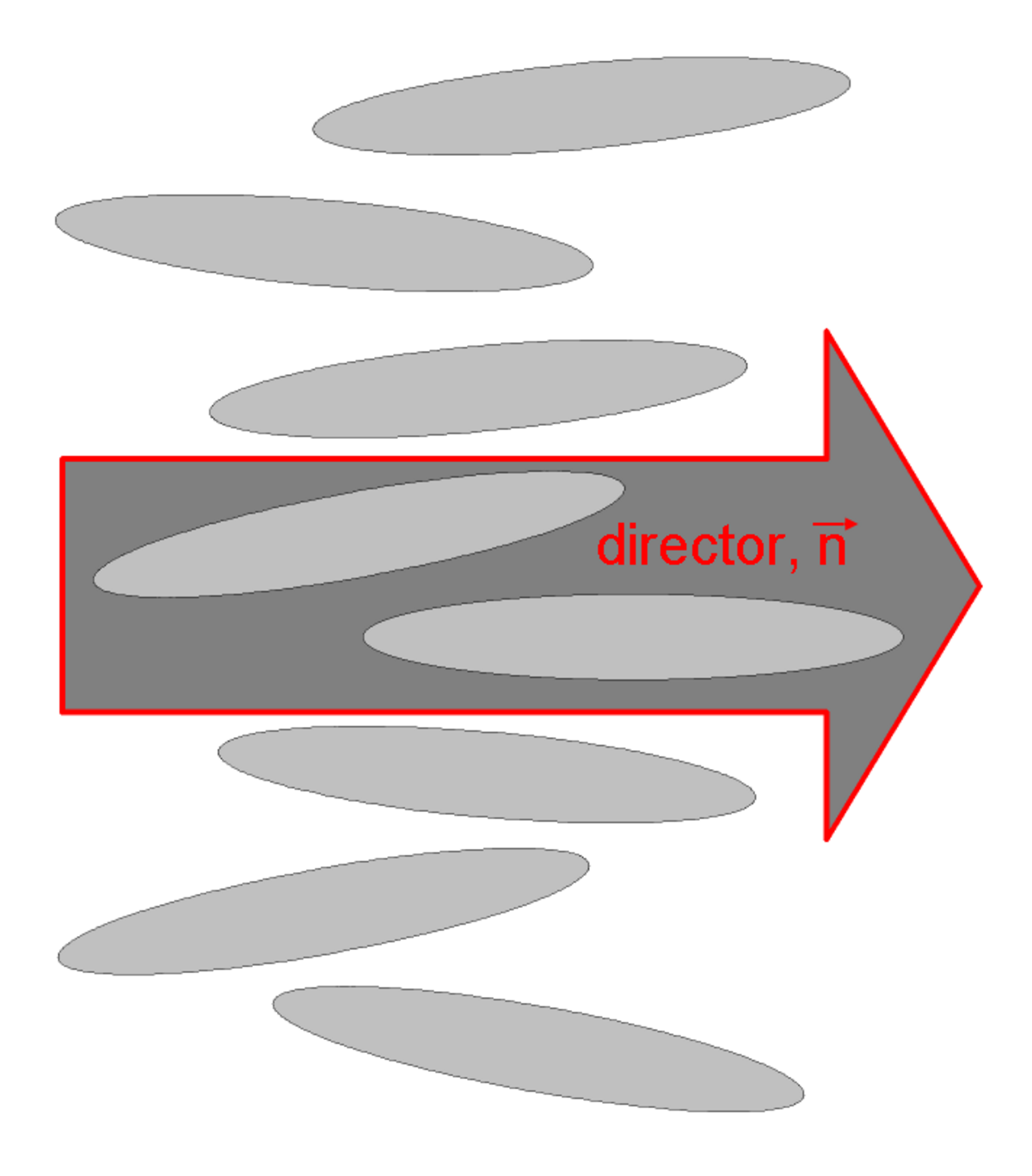
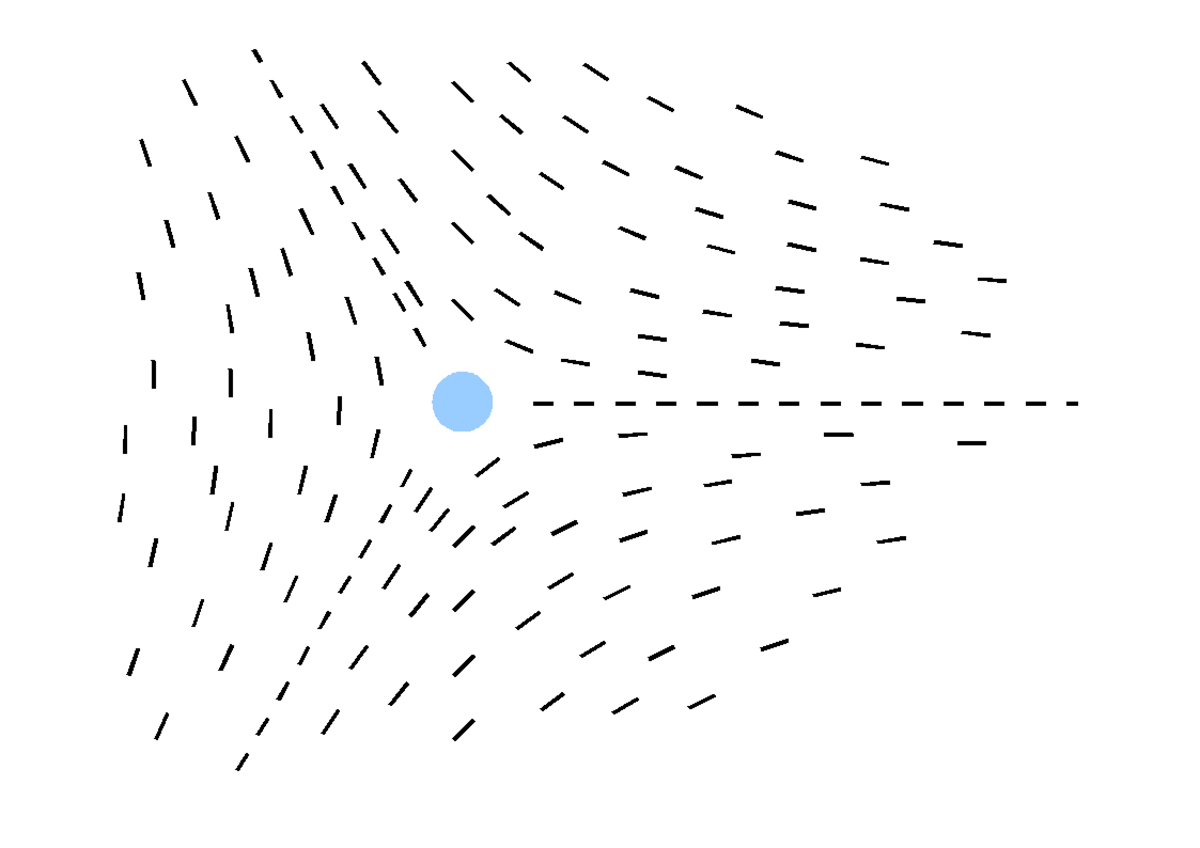
Les solutions θ=constante correspondent à un champ uniforme. Les solutions sont du type θ= m φ + constante où tg(φ) = y / x avec m entier ou demi-entier (car le directeur est défini à π près), la constante correspondant à une rotation du directeur. Cette équation permet de tracer les configurations du directeur correspondant aux différentes disinclinaisons observées, avec une singularité au centre.

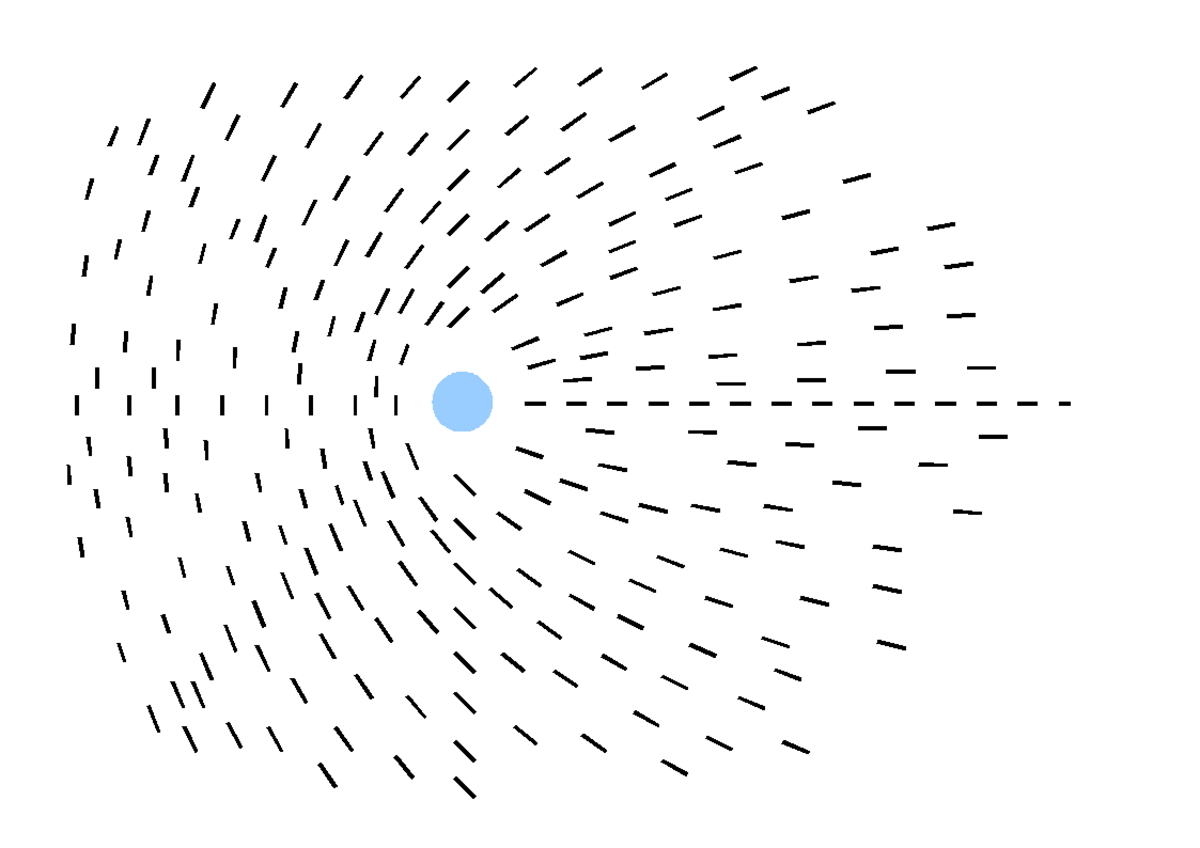
L'énergie par unité de longueur de la distorsion s'écrit finalement :

où r_c est le rayon de coupure (de l'ordre de la dimension moléculaire) que l'on peut estimer en comparant l'énergie du nématique à celle de la phase isotrope. De plus, comme l'énergie libre dépend de m², les configurations avec m petit sont plus favorables.