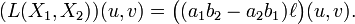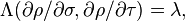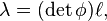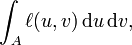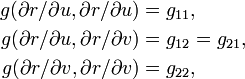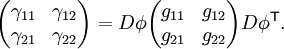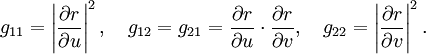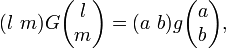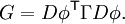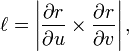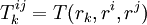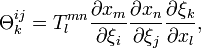Champ (mathématiques) - Définition

Champ scalaire

Il n'y a guère de difficulté à concevoir un champ scalaire, à partir d'un exemple physique : la température dans une cuisine. Il fait chaud à côté des radiateurs en hiver, et à côté des appareils de cuisson, quand ils fonctionnent. Il fait chaud aussi près d'une casserole chaude, ou d'une cafetière qui vient d'être remplie. Mais il fait froid dans les assiettes où on vient de poser deux boules de glace. En revanche, il fait chaud derrière le frigo. N'oublions pas que s'il y a des gens, l'air chauffe au contact de leur peau, et de leur vêtement, sauf par un jour de canicule.

La température est bien un nombre qui varie en fonction du lieu et du temps.

Champ de tenseurs sur une surface

Maintenant qu'on a compris ce qu'est un champ de vecteurs et un champ de covecteurs sur une surface S, on peut définir un champ de tenseurs sur cette même surface, en considérant plusieurs exemples.

On commence par un cas très utile : un champ de tenseurs qui permet de décrire l'élément d'aire. On définit en chaque point de S une forme bilinéaire alternée L(u,v) par son action sur les paires de vecteurs tangents. Il suffit pour cela de connaître l'action de L sur les deux vecteurs et  :

,

étant une fonction de u et v. A ce moment-là, si X_j désigne un champ de vecteurs tangent, pour avec pour coordonnées a_j et b_j, on aura

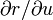
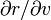
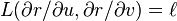
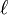
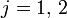
La formule de changement de carte se déduit au moyen du raisonnement du paragraphe précédent : si en coordonnées grecques, la même forme bilinéaire est définie par

alors

la vérification étant immédiate.

On peut alors définir une mesure signée sur S en posant, pour A une partie mesurable de S que la mesure de A est donnée par

pourvu que A soit entièrement contenu dans un ouvert admettant la paramétrisation par r(u,v). Si ce n'est pas le cas, on découpe A en une réunion disjointe d'ensembles mesurables, chacun d'eux étant contenu dans l'image d'une représentation paramétrique. Les détails de ce découpage importent peu, en vertu des formules de changement de variable.

On remarque que si tous les changements de carte, c'est-à-dire les φ ont des matrices de déterminant positif, et si les sont tous positifs, la mesure ainsi définie est positive.

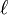
On passe maintenant à un autre cas pratique : des tenseurs symétriques contravariants et des tenseurs symétriques covariants.

Un tenseur symétrique covariant g est connu par son action sur les vecteurs de base :

les g_ij étant des fonctions de u et v.

Le changement de carte respecte les principes précédents : si le même tenseur covariant a des coordonnées γ_ij dans les coordonnées latines, et on trouve

Ici le signe en exposant désigne la transposition.

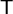
En particulier, si la matrice des coefficients de g est définie positive, il en est de même de la matrice des coefficients de γ.

Prenons comme tenseur covariant celui qu'induit la topologie euclidienne, c'est-à-dire :

Dans ce cas, la longueur d'un vecteur tangent, dont on connaît les coordonnées locales a et b est donnée par g₁₁a² + 2g₁₂ab + g₂₂b².

On peut aussi définir un tenseur symétrique contravariant, qui servira à mesurer la longueur des vecteurs cotangents. On remarque qu'il est possible de transformer un vecteur tangent en vecteur cotangent à l'aide du tenseur métrique covariant. Il suffit de poser , et on vérifie facilement que les changements de variable se font dans le sens covariant.

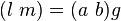
Il serait commode dans ce cas que la longueur de mesurée à l'aide du tenseur métrique contravariant soit égale à la mesure de par le tenseur métrique covariant, et cela revient à écrire

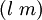
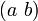
et comme cette relation doit avoir lieu pour tout choix de vecteur tangent de coordonnées a,b, cela revient à demander l'identité matricielle gGg = g, qui revient à imposer que la matrice du tenseur G soit l'inverse de la matrice du tenseur g.

Une fois G ainsi défini, on vérifie immédiatement que le changement de carte est donné par

L'élément de volume peut être, lui aussi, déduit du contexte euclidien. Il suffit de poser

en notant le produit vectoriel ordinaire.

On peut définir un tenseur de n'importe quelle variance sur la surface S. Par exemple un tenseur deux fois covariant et une fois contravariant sur S sera en chaque point de S une application trilinéaire du produit de l'espace tangent par deux copies de l'espace cotangent dans . Notons la base de l'espace tangent et définissons une base de l'espace cotangent par r_i(r^j) = δ_ij.

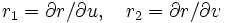
A ce moment-là, un tenseur T une fois contravariant et deux fois covariant est défini par son action sur tout triplet r_i,r^j,r^k, donc par le tableau de nombres

et la formule du changement de cartes peut être écrite

en utilisant la convention de sommation des indices répétés, c'est-à-dire en sommant dans le deuxième membre par rapport à l,m et n.