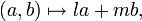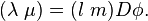Champ (mathématiques) - Définition

Champ de vecteurs cotangents sur une surface

On considère encore la surface S du paragraphe précédent, mais au lieu de définir un champ de vecteurs tangents, on définit un champ de formes linéaires, agissant sur les vecteurs tangents. En d'autres termes, pour chaque (u,v) dans , on définit une paire (l(u,v),m(u,v)) de nombres réels, et on définit l'action de cette forme linéaire par

pour tout champ de vecteurs tangent de coordonnées a,b.

Comme précédemment, on peut se poser la question d'un changement de coordonnées locales. Supposons que dans les coordonnées (σ,τ), le même champ de formes linéaires ait les coordonnées λ(σ,τ),μ(σ,τ). On doit alors avoir

(la + mb)(φ(σ,τ)) = (λα + μβ)(σ,τ),

pour tout champ tangent.

On suppose que (a,b) et (α,β) sont liés par la relation

.

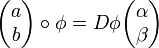
Un calcul élémentaire fournit alors

On constate que le changement de coordonnées pour les formes linéaires « va dans le sens contraire » du changement de coordonnées pour les vecteurs.

Les champs de formes linéaires sont aussi appelés, en particulier par les physiciens « vecteurs covariants », puisque le changement de variable va dans le même sens que la transformation φ : φ va des coordonnées grecques aux coordonnées latines, et le champ de formes linéaires en coordonnées latines s'exprime en fonction des coordonnées grecques et de la matrice jacobienne de φ. En revanche, les coordonnées grecques d'un champ de vecteurs s'expriment en fonction des coordonnées latines de celui-ci et de la matrice jacobienne de φ.

Si on adopte des notations indexée, avec x_i et ξ_j comme au paragraphe précédent, et en remplaçant respectivement par l¹,l² et par λ¹,λ², la formule de changement de coordonnées devient

,

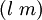
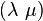
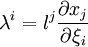
avec la convention de sommation des indices répétés.

Remarquons que la physique fournit une abondance de champs qui doivent être considérés comme cotangents. L'exemple le plus connu est le champ électrique, puisque, du point de vue dimensionnel, c'est une différence de potentiel par unité de longueur. De plus, il a les propriétés qu'on attend dans cette situation : c'est un vecteur qu'on peut intégrer agréablement le long d'une courbe de l'espace, en en prenant le produit scalaire avec le vecteur tangent. Cette propriété est caractéristique d'une forme différentielle de degré 1. Elle sera vérifiée pour tout champ dérivant d'un potentiel scalaire.

Les mathématiciens construisent un nouvel objet : on attache tous les espaces vectoriels de formes linéaires cotangentes à la surface S et on obtient ce qu'on appelle le fibré cotangent à S.

Champs sur des variétés

La définition de champs sur des variétés est une généralisation des définitions et des calculs précédents.

La plupart des variétés différentielles dont on se sert en pratique peuvent être plongées dans un espace de dimension finie (Théorème de Whitney), mais on peut se représenter une variété abstraite comme suit : elle est formée de morceaux ouverts de l'espace , avec des lois de recollement. Plus précisément, on se donne des ouverts U_i de , et pour toute paire i,j d'indices distincts des applications lisses φ_ij allant d'un ouvert V_ij de U_i dans un ouvert V_ji de U_j, sous les conditions suivantes :

1. est l'application identité de V_ij ;
2. est l'application identité sur son ensemble de définition pour tout triplet d'indices distincts i,j et k.

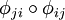
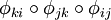
On définit alors une relation d'équivalence sur la réunion disjointe des U_j en posant

si x = y ou si x et y appartiennent respectivement a V_ij et V_ji et l'on a la relation y − φ_ij(x).

En d'autres termes, les U_i sont des morceaux de caoutchouc, on doit coller la languette V_ij sur la languette V_ji en appliquant chaque point x sur un point y = φ_ij(x). Bien sûr il faut que tout ceci reste compatible là où il y a collage de trois languettes ensemble (ou plus), et cela est assuré par la deuxième relation.

La réflexivité et la symétrie de cette relation sont immédiate ; pour la transitivité, il faut remarquer que si y = φ_ij(x) et z = φ_jk(y), alors la deuxième condition sur les φ_ij implique que x = φ_ki(z).

La variété abstraite est alors simplement le quotient de la réunion disjointe des U_j par cette relation d'équivalence.

Pour passer au fibré tangent, et donc définir des champs tangents, on peut se contenter de considérer la réunion disjointe des et la relation d'équivalence (x,v)˜(y,w) s'il y a égalité ordinaire ou si x est dans V_ij, y dans V_ji, y = φ_ij(x),w = Dφ_ij(x)v. C'est une relation symétrique et réflexive. On obtient la transitivité en différentiant la relation .

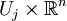
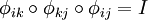
Pour passer au fibré cotangent, on part aussi de la somme disjointe des , mais cette fois-ci la relation d'équivalence entre (x,l) et (y,m), avec l et m des formes linéaires, impose m = lDφ_ij.

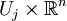
On laisse au lecteur le soin d'imaginer ce qui se passera avec un tenseur de n'importe quel ordre, c'est-à-dire une forme k-linéaire, j fois contravariante et k − j fois covariante, ou de se reporter à l'article tenseur.