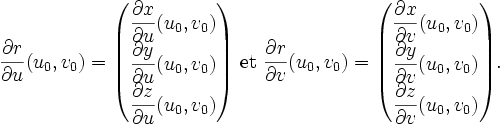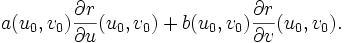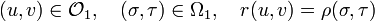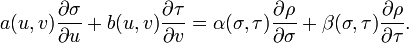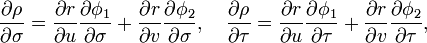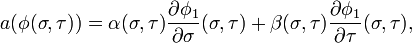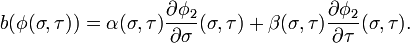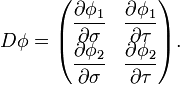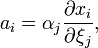Champ (mathématiques) - Définition

Introduction

Un champ est une application qui associe aux points d'un objet, généralement multidimensionnel, des valeurs scalaires, vectorielles ou tensorielles.

Vision physique et vision mathématique des champs

La notion de champ est d'origine physique, et elle sert à décrire des quantités variant en fonction de leur point de définition : champ de température, champ de densité, champ de vitesse, champ de forces, champ de pression, champ de gravitation, champ électrique, champ magnétique.

Comme la physique s'intéresse à des phénomènes d'observation, un des fondements de l'étude des champs en physique est la notion suivante de symétrie : quel que soit le choix du système de coordonnées qu'on choisit pour faire une description analytique, les phénomènes physiques ne changent pas.

Cette notion permet aux mécaniciens et aux physiciens de faire une différence entre vecteurs et pseudo-vecteurs. Les seconds changent de sens avec l'orientation de l'espace, et du point de vue mathématique, une vision simple consiste à définir les pseudo-vecteurs comme un couple formé d'un vecteur et d'un signe, + ou -, avec une relation d'équivalence , le signe étant caractéristique de l'orientation de l'espace. Une vision plus savante dira qu'un pseudovecteur est une densité, c'est-à-dire un tenseur d'une espèce particulière.

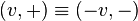
Plus généralement, que ce soit en mécanique classique ou relativiste, on a besoin de prendre des coordonnées curvilignes. La notion de covariance d'un champ exprime précisément que la physique est indépendante du choix de coordonnées. Il sera donc implicite pour un physicien qu'un champ est covariant.

Mais les mathématiciens décomposent ces notions, et en particulier ils ne posent pas d'entrée de jeu qu'un champ satisfait des propriétés de symétrie et, en particulier, de covariance. En revanche, ils vont prendre de multiples précautions pour décrire un champ dans le cas non scalaire, c'est-à-dire vectoriel ou tensoriel, dans le but de construire des notions intrinsèques, c'est-à-dire indépendantes du choix de coordonnées.

Ainsi, si est un ouvert de l'espace , un champ scalaire est une application de dans , et un champ vectoriel ou champ de vecteurs est une application d' dans . Enfin un champ de tenseurs est une application de dans l'espace vectoriel des applications k-linéaires de dans . Dans cette dernière définition, V est un espace de dimension p, V ^* est son dual, il y a j facteurs V et k − j facteurs V ^* , avec bien sûr .

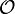
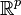
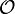
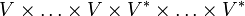
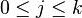
Il existe des versions complexes de cet ensemble de définitions : il suffit de remplacer par dans les ensembles d'arrivée.

Champ de vecteurs tangents sur une surface

L'exemple physique le plus simple d'un champ de vecteurs tangent est celui d'un champ de vitesses : si des particules se déplacent sur une surface qui n'est pas plane, leurs vitesses sont tangentes à la surface. En supposant ces particules si fines et si nombreuses qu'on puisse les représenter par un modèle continu, leurs vitesses moyennes dans de très petits volumes donnent une bonne idée de ce que serait un champ de vecteurs tangent à la surface.

Avant de développer la notion de champ sur une variété abstraite, il faut étudier un cas concret : un champ de vecteurs tangent sur une surface S plongée dans . Localement, elle peut être paramétrée par trois fonctions continûment différentiables x(u,v),y(u,v),z(u,v), avec (u,v) dans un ouvert de .

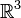
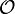
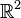
Notons pour simplifier

.

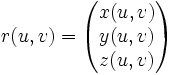
Les r(u,v) forment donc un champ de vecteurs à 3 composantes sur .

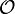
Le plan tangent en x₀ = x(u₀,v₀),y₀ = y(u₀,v₀),z₀ = z(u₀,v₀) est engendré par les vecteurs

si ces deux vecteurs sont indépendants. On fait cette hypothèse systématiquement. Cette condition porte sur la nature de la description par les fonctions x,y,z de u et v.

Par conséquent, un vecteur tangent en x₀,y₀,z₀ à la surface est une combinaison linéaire de la forme

Les coordonnées locales d'un champ tangent à la surface S sont donc un couple de deux nombres a(u,v) et b(u,v).

Si localement, S admet un autre paramétrage ξ(σ,τ),η(σ,τ),ζ(σ,τ), avec (σ,τ) dans un ouvert Ω, on note ρ le champ de vecteurs de coordonnées ξ, η, ζ.

Un champ de vecteur tangent aura pour coordonnées α(σ,τ) et β(σ,τ) dans ce choix de coordonnées locales.

Supposons, de plus, que l'image par r de recoupe l'image ρ(Ω) par ρ de Ω. Il est alors légitime de se demander comment sont reliées les coordonnées a,b et les coordonnées α,β.

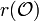
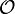
On montre, au moyen du théorème des fonctions implicites que l'identité

r(u,v) = ρ(σ,τ)

avec les conditions

sont des vecteurs indépendants

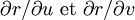
et

sont des vecteurs indépendants

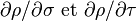
implique l'existence locale d'un difféomorphisme entre (σ,τ) et (u,v).

Plus précisément, pour tout choix de (σ₀,τ₀) et (u₀,v₀) satisfaisant la relation r(u₀,v₀) = ρ(σ₀,τ₀), on peut trouver deux voisinages ouverts respectifs de (u₀,v₀) et (σ₀,τ₀), et , et deux applications continûment différentiables φ de Ω₁ dans et ψ de dans Ω₁ tels que la relation

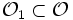
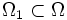
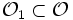
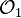
implique

Si un champ tangent a pour coordonnées (a,b) dans et (α,β) dans Ω₁, alors on peut écrire l'identité

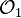
On différentie la relation r(φ(σ,τ)) = ρ(σ,τ) par rapport à σ et τ, et on obtient, grâce au théorème de dérivation des fonctions composées :

et si on substitue ces identités dans la relation donnant les deux représentations du champ de vecteurs, on trouve

On a simplement utilisé le fait que et forment une base.

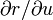
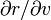
Une autre manière de noter la relation entre (a,b) et (α,β) consiste à utiliser la matrice jacobienne

Avec cette notation, il vient

.

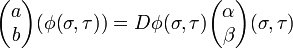
On peut noter un peu différemment ce qui précède. Si on remplace (u,v) par x₁,x₂ et σ,τ par ξ₁,ξ₂, et de même a,b par a₁,a₂ et α,β par α₁,α₂, alors la formule du changement de carte ci-dessus devient

avec la convention de sommation des indices répétés ; on somme dans la formule ci-dessus, par rapport à j.

Le point de vue des physiciens est que la relation ci-dessus caractérise un champ de vecteurs tangents sur la surface S. Le point de vue des mathématiciens est un peu différents : il consiste à voir la surface S et la collection de ses plans tangents en chaque point comme un nouvel objet : le fibré tangent à S. Bien sûr, cela revient au même, il faut seulement être conscient de cette terminologie en lisant la littérature.