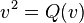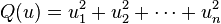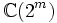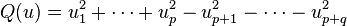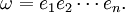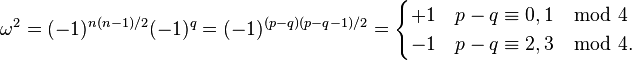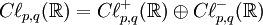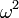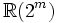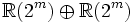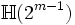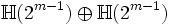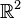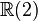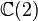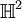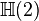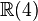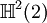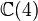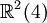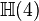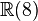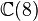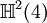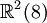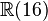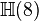Classification des algèbres de Clifford - Définition

Introduction

En mathématiques, en particulier dans la théorie des formes quadratiques non dégénérées sur les espaces vectoriels réels et complexes, les algèbres de Clifford de dimension finie ont été complètement classées. Dans chaque cas, l'algèbre de Clifford est isomorphe à une algèbre de matrices sur , , ou (les quaternions), ou à une somme directe de deux de ces algèbres, bien que ce ne soit pas la manière canonique.

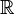
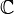
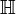
Notation et conventions. Dans cet article, nous utiliserons la convention de signe (+) pour la multiplication de Clifford, c’est-à-dire

pour tous les vecteurs , où Q est la forme quadratique sur l'espace vectoriel V. Nous désignerons l'algèbre de matrices avec les entrées dans l'algèbre de division K par K(n). La somme directe des algèbres sera désignée par K²(n) = K(n) ⊕ K(n).

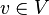
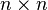
Le cas complexe

Le cas complexe est particulièrement simple : chaque forme quadratique non dégénérée forme sur un espace vectoriel complexe est équivalente à la forme diagonale standard

où n = dim V, donc, il existe essentiellement une seule algèbre de Clifford dans chaque dimension. Nous noterons l'algèbre de Clifford sur avec la forme quadratique standard par .

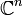
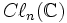
Il existe deux cas séparés à considérer, suivant que n est pair ou impair. Lorsque n est pair, l'algèbre est centrale simple et donc, par le théorème d'Artin-Wedderburn est isomorphe à l'algèbre de matrice sur . Lorsque n est impair, le centre inclus non seulement les scalaires mais aussi les pseudoscalaires (éléments de degré n). Nous pouvons toujours trouver un pseudoscalaire normalisé tel que . Définissons les opérateurs

.

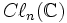
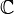
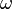
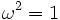
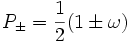
Ces deux opérateurs forment un ensemble complet d'éléments idempotents orthogonal, et puisqu'ils sont centraux, ils donnent une décomposition de en une somme directe de deux algèbres

où .

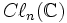
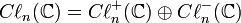
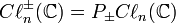
Les algèbres sont simplement les espaces propres positifs et négatifs d' et les sont simplement les opérateurs de projection. Puisque est impair, ces algèbres sont mélangées par  :

.

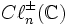
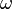
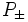
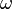
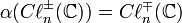
et par conséquent isomorphes (puisque est un automorphisme). Ces deux algèbres isomorphes sont chacune simple centrale et donc, de nouveau, isomorphes à une algèbre de matrices sur . Les tailles de ces matrices peuvent être déterminées à partir du fait que la dimension de est . Ce que nous obtenons alors, c'est la table suivante :

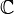
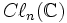
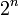
n
2m
2m+1

La sous-algèbre paire de est (non-canoniquement) isomorphe à . Lorsque n est pair, les sous-algèbres paires peuvent être identifiées avec les matrices diagonales en blocs (lorsqu'elles sont séparées en matrice en bloc 2 ×2). Lorsque n est impair, les sous-algèbres paires sont ces éléments de pour lesquels les deux facteurs sont identiques. En rassemblant l'une et l'autre pièce, cela donne un isomorphisme avec .

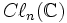
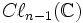
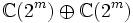
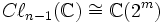
Le cas réel

Le cas réel est légèrement plus compliqué, exhibant une périodicité 8 plutôt que 2. Chaque forme quadratique non dégénérée sur un espace vectoriel réel est équivalent à la forme diagonale standard :

où n = p + q est la dimension de l'espace vectoriel. La paire d'entiers (p, q) est appelée la signature de la forme quadratique. L'espace vectoriel réel avec cette forme quadratique est souvent noté . L'algèbre de Clifford sur est notée .

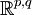
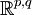
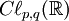
Une base orthonormale standard {e_i} pour consiste en n = p + q vecteurs mutuellement orthogonaux, p est de norme +1 et q est de norme -1. L'algèbre aura par conséquent p vecteurs dont le carré sera +1 et q vecteurs dont le carré sera -1. L'unité pseudoscalaire dans est définie par

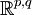
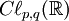
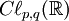
Le carré d' est donné par

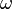
À noter, à la différence du cas complexe, qu'il n'est pas toujours possible de trouver un pseudoscalaire dont le carré est +1.

La classification s'ensuit : si n est paire (de manière équivalente, si p - q est pair) l'algèbre est simple centrale et donc est isomorphe à une algèbre de matrices sur ou par le théorème d'Artin-Wedderburn. Si n (ou p - q) est impair, alors l'algèbre n'est pas simple centrale mais possède plutôt un centre qui inclut les pseudoscalaires aussi bien que les scalaire. Si n est impair et alors, comme dans le cas complexe, l'algèbre se décompose en une somme directe d'algèbres isomorphes

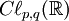
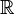
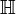
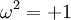
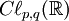
chacune est simple centrale et donc isomorphe à l'algèbre de matrice sur ou . Si n est impair et alors le centre de est isomorphe à et peut être considérée comme une algèbre complexe. Comme une algèbre complexe, elle est simple centrale et donc, isomorphe à une algèbre de matrice sur .

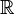
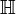
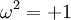
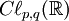
Tout indique qu'il existe trois propriétés qui déterminent la classe de l'algèbre  :

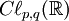
• n est pair/impair,
• ,
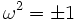
• La classe de Brauer de l'algèbre (n pair) ou de la sous-algèbre paire (n impair) est ou .

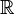
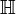
Chacune de ces propriétés dépend seulement de la signature p - q modulo 8. La table de classification complète est donnée ci-dessous. La taille des matrices est déterminée par la condition que ont une dimension .

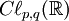
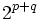
p - q mod 8			p - q mod 8
0	+		1	+
2	-		3	-
4	+		5	+
6	−		7	−

Ce qui suit est une table de cette classification pour p + q \le 8. Ici p + q est placé verticalement et p - q horizontalement (par ex. l'algèbre est trouvée ligne 4, colonne - 2).

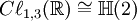
	8	7	6	5	4	3	2	1	0	- 1	- 2	- 3	- 4	- 5	- 6	- 7	- 8
0
1
2
3
4
5
6
7
8
	+	-	-	+	+	-	-	+	+	-	-	+	+	-	-	+	+

Il existe une toile embrouillée de symétrie et de relations dans la table ci-dessus. Par exemple, la table entière est symétrique par rapport à la colonne 1 (aussi bien que la colonne 5, - 3 et - 7). Se déplacer sur 4 emplacements dans n'importe quelle ligne donne une algèbre identique.