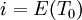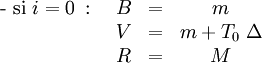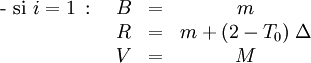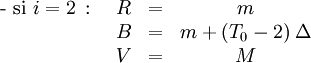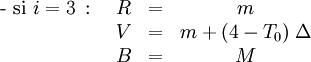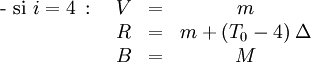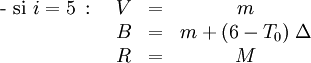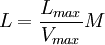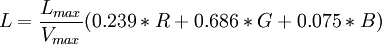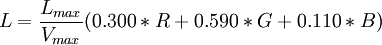Codage informatique des couleurs - Définition
La liste des auteurs de cet article est disponible ici.
Généralisation du modèle de couleur
Considérons l'espace à 3 dimensions basé sur les composantes
- Rouge,
- Vert, et
- Bleu
où tous les points ont une position définie dans un repère orthonormé par les 3 coordonnées (r,v,b).
L'œil humain n'est capable de percevoir qu'une partie de cet espace. L'ensemble des points de cet espace qui correspond aux possibilités visuelles de l'œil humain forme un volume convexe ou patatoïde, qui, projeté sur un plan convenablement orienté, donne une figure en forme de fer à cheval comme le montre l'image suivante, où les nombres à 3 chiffres, placés près du bord du fer à cheval, représentent les valeurs en nanomètres des longueurs d'onde associées aux couleurs monochromatiques saturées de l'arc-en-ciel :
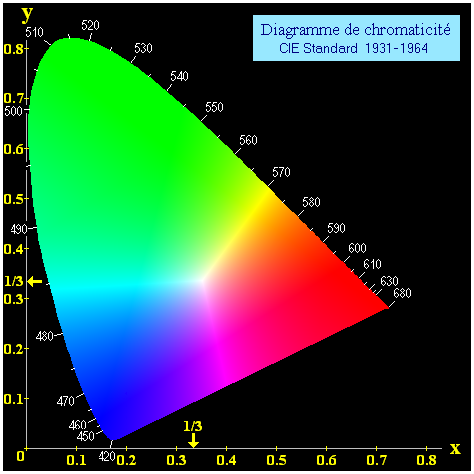
Ce patatoïde correspond à ce que l'on appelle le gamut de l'œil humain. La figure ci-dessous, qui représente pour chaque type de support d'image (film, moniteur d'ordinateur, imprimante) un gamut distinct (et toujours plus réduit que celui de l'œil humain) illustre bien la pauvreté de certains supports en termes de rendu réel des couleurs.
Maintenant, imaginons le cube de unitaire où M=(255,255,255). Suivant ce cube, M sera la couleur blanche tandis que (0,0,0) est noir. Si on se positionne maintenant suivant cet axe [OM) depuis le point M, on observe
- un disque autour de ce point dont la couleur passe du Rouge, puis au Vert au Bleu puis revient au Rouge (si on fait un tour complet) avec tous les intermédiaires.
- suivant les rayons de ce disque, la couleur est pastel vers le centre et saturée vers le bord.
- suivant l'axe [OM), on a une couleur qui est claire en allant vers M et sombre à allant vers O.
On a retrouvé ainsi le repère TSL ou HSL.
Une façon de représenter ce repère est de projeter le rayon de saturation et l'angle de teinte sur un cylindre qui est déplié suivant sa hauteur, on obtient le schéma suivant :
La transformation RVB/TSL est une simple transformation de repère qui peut être réalisée par une série de rotations et de translations combinées avec un passage d'un système de coordonnées cartésiennes à un système de Coordonnées polaires ; Les correspondent à une transformation de ce type (parmi d'autres possibles).
On constate à partir de maintenant que la représentation dite en « RVB » ne peut proposer qu'un gamut réduit des possibilités :
- soit le cube propose des combinaisons inaffichables ou invisibles,
- soit le cube est inscrit dans le patatoïde.
Le choix pratiqué a été le second. On a donc cherché d'autres formes de repères qui permettent d'agrandir le gamut.
Par exemple, si on utilise pour r, v et b des réels au lieu d' entiers, on peut obtenir un dégradé de teintes parfait car continu.
En outre, le recours à une échelle logarithmique plutôt que linéaire permettra d'obtenir plus de dynamique sur une zone choisie.
Par ces artifices, il devient dès lors possible de disposer de plus d'informations que le support (voire l'œil) ne peut en afficher.
Cette catégorie de procédés appartient aux images dites HDR.
Formules de changement de système de codage
RVB vers TSL
Voici maintenant les formules mathématiques qui régissent le passage des coordonnées R, G, B d'une couleur donnée aux coordonnées T, S, L de la même couleur, et réciproquement (les formules ci-dessous correspondent notamment sous Windows au codage utilisé dans l'utilitaire Paint livré avec les divers systèmes d'exploitation de Microsoft tournant avec des processeurs en 32 bits) :
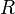
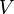
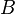

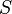
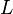
- Calcul de la teinte

On doit d'abord calculer les 3 grandeurs préalables suivantes :
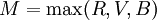
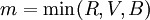
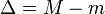

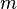
puis la valeur de
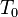
- si R est supérieur à V et à B :
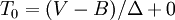
- si V est supérieur à B et à R :
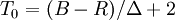
- si B est supérieur à R et à V :
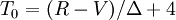
et enfin, en déduire la teinte

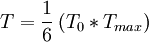
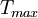
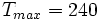
- Calcul de la saturation
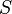
- si
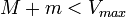
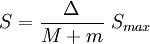
- si
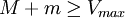
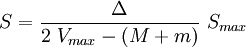
avec
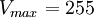
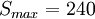
- Calcul de la luminance
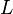
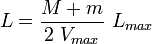
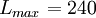
Remarques : les formules donnant la valeur de la teinte

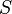
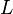
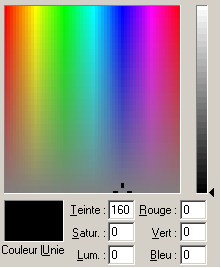
- si R, V et B sont tous égaux, alors T est égal à 160 (dans Paint) et S est égal à 0 (teinte grise complètement désaturée), et réciproquement ;
- si R, V et B sont tous égaux à 0, alors L est égal à 0 (noir absolu), et réciproquement ;
- si R, V et B sont tous égaux à
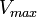
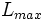
Voici donc quelques variantes:
- pour la luminance:
-
- pour la saturation:
-
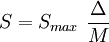
-
Note :
TSL vers RVB

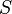
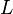
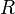
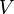
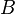
- Calculs préalables : on doit commencer, comme dans le cas précédent, par calculer les 4 grandeurs intermédiaires
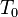

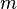

Sachant que l'on a :
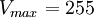
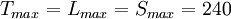
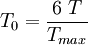
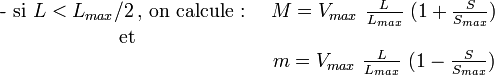
![\begin{matrix}\mbox{- si }L \ge L_{max}/2\,\mbox{, on calcule : } & M=V_{max}\ \left [\frac{L}{L_{max}}\ (1-\frac{S}{S_{max}})+\frac{S}{S_{max}}\right ]\\\mbox{et} & \ \\ \ & m=V_{max}\ \left [\frac{L}{L_{max}}\ (1+\frac{S}{S_{max}})-\frac{S}{S_{max}}\right ] \end{matrix}](https://static.techno-science.net/illustration/Definitions/autres/c/c8084046d3f662d832ff622ce2febbc6_2553299a27461778340b4d251a9e1672.png)
d'où l'on peut tirer :
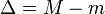
Il devient dès lors possible de déterminer les valeurs des 3 composantes
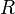
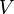
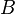
Note :
![M = V_{max}\ \left [\frac{L}{L_{max}}\right ]\](https://static.techno-science.net/illustration/Definitions/autres/8/8d23df6a5591922e497472e13952fcab_4ca1e6421b0ad33bb1120a99e1f74387.png)
puis
![\Delta = M\ \left [\frac{S}{S_{max}}\right ]\](https://static.techno-science.net/illustration/Definitions/autres/2/27d40596b65badf59e1b367fd6f71555_472444d42a0ddcf4afdc8bbf1a6090ce.png)
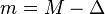
.
- Calcul des trois composantes
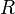
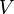
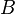
Les formules à utiliser dépendent de la valeur de la partie entière de
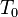
Soit :