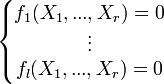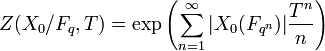Conjectures de Weil - Définition

Énoncé des conjectures de Weil

Soit f₁(X₁,...,X_r),...,f_l(X₁,...,X_r) des polynômes à coefficients entiers. On peut projeter ces polynômes dans n'importe quel corps fini F_q, simplement si q = p^k en prenant les coefficients de ces coefficients modulo p. En fait, on cherche à étudier les racines d'un système d'équations polynômiales

On peut donc considérer l'ensemble des solutions du système étudié, où les polynômes sont à coefficients dans F_q. Les conjectures de Weil nous donnent de nombreuses informations lorsque l'on s'intéresse au nombre de ces solutions. Formalisons cette idée.

Ces équations définissent une variété algébrique sur F_q, où ce qui revient au même, un schéma séparé de type fini sur F_q. En effet, si on considère l'idéal I = (f₁,...,f_l) de F_q[X₁,...,X_r], soit A = F_q[X₁,...,X_r] / I, alors le schéma sur F_q est le spectre d'anneau de A, X = SpecA. L'ensemble des solutions du système ci-dessus dans est en bijection avec , de manière que le problème initial devient le calcul de | X(F_q) | .

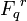
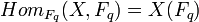
On notera par la suite X₀ = | X(F_q) | . Lorsqu'on considérera X₀ comme une variété sur , on notera: .

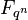
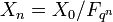
L'objet essentiel d'étude apparaissant dans les conjectures de Weil est la fonction zêta de X_n = X₀ / F_q, c'est une série formelle à coefficients rationnels définie comme suit:

où est le nombre de points rationnels de X_n = X₀ / F_q, c'est-à-dire le nombre de solutions dans du système d'équations.

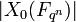
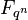
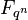
Conjectures de Weil: Si X₀ / F_q est lisse (c'est-à-dire si les équations ne possèdent pas de singularité) et projective (c'est-à-dire si les équations polynomiales sont homogènes) de dimension d alors:

1. Z(X₀ / F_q,T) est une fonction rationnelle de T à coefficients dans .
2. Équation fonctionnelle : Il existe des entiers K et tels que:
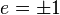
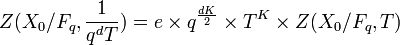
3. Hypothèse de Riemann sur les corps finis : la fonction zêta de X₀ / F_q se met sous la forme: où P_i, , est un polynôme de Weil de poids i. De plus, on a avec .
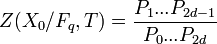
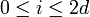
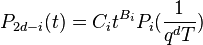
4. Lien avec la topologie : Si X₀ / F_q est la projection sur F_q d'une variété projective complexe non-singulière V^an, alors le degré de P_i est le i-ème nombre de Betti de V^an. Plus précisément, soir R un anneau muni d'un morphisme surjectif et d'un morphisme injectif . Soit M un R-schéma propre et lisse tel que et . On a alors pour tout i, .

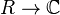
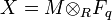
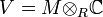
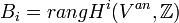
La partie rationnelle (la rationalité de la fonction zêta) fut démontrée par Bernard Dwork en 1959 grâce à des méthodes p-adiques. C'est véritablement le travail de Grothendieck qui inspirera plus tard Deligne pour mettre un point final à la démonstration. En effet, Grothendieck rénove la géométrie algébrique en se lançant dans un travail monumental duquel sortiront ses Éléments de géométrie algébrique. Par cet ouvrage, d'une extrême généralité, il étend la géométrie algébrique : il l'étend en particulier à l'étude d'équations définies sur des anneaux, et non sur des corps comme on le faisait auparavant, ce qui permet d'attaquer les problèmes posés sur les entiers. Il démontrera ainsi en 1963-1964 les points 1., 2. et 4. par une démonstration différente de celle de Dwork. En ce qui concerne l'hypothèse de Riemann, beaucoup plus délicate, il faut attendre 1973 pour que Pierre Deligne, inspiré surtout par les travaux de Weil, Serre et Grothendieck, propose une démonstration.

La cohomologie de Weil

Weil suggéra que les conjectures découlaient de l'existence d'une "théorie cohomologique de Weil" appropriée pour les variétés sur les corps finis, similaire à la cohomologie usuelle avec des coefficients rationnels pour les variétés complexes. Son idée était que si F est l'automorphisme de Frobenius sur le corps fini, alors le nombre de points de la variété X sur le corps d'ordre q^m est le nombre de points fixés de F^m (agissant sur tous les points de la variété X définis sur la clôture algébrique). En topologie algébrique, le nombre de points fixés d'un automorphisme peut être établi en utilisant le théorème du point fixe de Lefschetz, donnant une somme alternée des traces sur les groupes cohomologiques. Donc, s'il existait des groupes cohomologiques similaires pour les variétés sur les corps finis, alors la fonction zêta pourrait être exprimé en termes de ceux-ci.

Le premier problème avec ceci est que le corps de coefficient pour une théorie cohomologique de Weil ne peut pas être le corps des nombres rationnels. Pour voir ceci, considérons le cas d'une courbe elliptique supersingulière sur un corps fini de caractéristique p. L'anneau d'endomorphisme de ceci est une algèbre de quaternion sur les rationnels, et agirait sur le premier groupe cohomologique, qui serait un espace vectoriel à 2 dimension sur le corps de coefficient par analogie avec le cas d'une courbe elliptique complexe. Néanmoins, une algèbre de quaternion sur les rationnels de peut pas agir avec un espace vectoriel à deux dimensions sur les rationnels. Le même argument élimine la possibilité que le corps de coefficient soit le corps des réels ou les nombres p-adiques, parce que l'algèbre de quaternion est encore une algèbre de division sur ces corps. Néanmoins, il n'élimine pas la possibilité que le corps de coefficient soit le corps des nombres l-adiques pour quelques nombres premiers l≠p, parce que sur ces corps l'algèbre de division se sépare et devient une algèbre matricielle, qui peut agir sur un espace vectoriel à 2 dimensions. Grothendieck et Michael Artin sont parvenus à construire des théorie cohomologiques appropriées sur le corps des nombres l-adiques pour chaque nombre premier l≠p, appelée cohomologie l-adique.