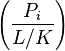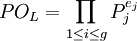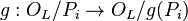Décomposition des idéaux premiers dans les extensions galoisiennes - Définition

Introduction

En mathématiques, l'interaction entre le groupe de Galois d'une extension galoisienne de corps de nombres (ou de corps de nombres p-adiques, ou de corps de fonctions), et la manière dont les idéaux premiers de l'anneau des entiers algébriques factorisent sous forme de produits d'idéaux premiers de , est à la base de nombreux développement fructueux en théorie algébrique des nombres.

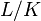
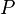
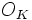
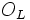
Le cas d'une extension non nécessairement galoisienne est traitée dans l'article Décomposition des idéaux premiers. Les notions d'extension ramifiée, d'extension décomposée y sont envisagées ; ces notions doivent certainement être familière pour aborder la lecture du présent article. Dans le cas d'une extension galoisienne, la structure supplémentaire se traduit au niveau de ces propriétés, via, certains sous-groupes du groupe de Galois : le groupe de décomposition et le groupe d'inertie, mais aussi les groupes de ramification supérieurs.

Ces notions sont quelquefois attribuées à David Hilbert par l'appellation théorie d'Hilbert. Il existe une analogie géométrique, la ramification des surfaces de Riemann, qui est plus simple du fait qu'une seule sorte de sous-groupe de doit être considéré, plutôt que deux. Ceci était certainement familier avant Hilbert.

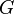
Les propriétés fondamentales

Sur les indices

Soit la factorisation d'un idéal premier P de O_K dans O_L :

comme un produit d'idéaux premiers distincts , avec les indices de ramification , alors agit transitivement sur . C’est-à-dire, les facteurs idéaux premiers de P dans L forment une orbite unique sous les automorphismes de L sur K. L'unicité de la décomposition en produit d'idéaux premiers permet alors de montrer que l'indice de ramification est indépendant de j. De même pour les degrés d'inertie f_j, en regardant cette fois l'action du groupe de Galois sur les corps résiduels (on explique plus en détail ci-dessous cette action, ce qui est plus technique). Ces deux assertions sont fausses en général pour les extensions non galoisiennes.

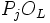
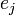
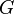
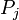
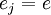
On obtient alors la relation suivante

[L:K] = n = efg

où g est le nombre d'idéaux premiers distincts intervenant dans la décomposition de l'idéal P.

Théorie de Galois

Cependant, la relation obtenue sur les indices ne traduit qu'une petite partie de la richesse introduite par la structure galoisienne. En effet, si g est un élément du groupe de Galois, alors g agit sur L en laissant K invariant, et, par restriction, O_L en laissant O_K invariant. Un idéal premier P_i de O_L au-dessus d'un idéal premier P de O_K étant donné, on vérifie facilement que l'action passe au quotient :

est un isomorphisme de O_K/P-espaces vectoriels entre les corps résiduels. Pour obtenir un automorphisme, il est intéressant de se restreindre au cas où g(P_i)=P_i. On appelle groupe de décomposition, noté D_Pi de l'idéal P_i l'ensemble des éléments du groupe de Galois qui vérifient cette relation. La relation fondamentale en termes de théorie de Galois devient alors :

où le morphisme de droite est celui qu'on vient de définir. Sa surjectivité constitue un théorème. Quant à son noyau, on le définit comme étant le groupe d'inertie. Ces objets contiennent l'information qui était codé par les indices de ramification et degré d'inertie dans le cas non galoisien : le cardinal du groupe d'inertie est l'indice de ramification, celui du groupe de décomposition est le produit du degré d'inertie et de l'indice de ramification

Application de la correspondance de Galois

Les sous-corps correspondant, par la correspondance de Galois, aux sous-groupes qu'on vient de définir, admettent une interprétation arithmétique simple : le groupe de décomposition correspond à l'extension totalement décomposée maximale, et le groupe d'inertie à l'extension non ramifiée maximale.

Le symbole d'Artin

Dans le cas d'une extension non ramifiée en un premier P_i, le groupe d'inertie est trivial, comme remarqué précédemment. La relation fondamentale devient alors un isomorphisme entre le groupe de décomposition en P_i et le groupe de Galois de l'extension des corps résiduels. Dans le cas où les corps résiduels sont finis, ce qui est vrai en particulier pour les corps de nombres et les corps de nombres p-adiques, le groupe de Galois de l'extension de corps résiduels est cyclique et admet un générateur privilégié : l'endomorphisme de Frobenius. Son image dans le groupe de décomposition est alors appelé symbole d'Artin pour le premier P_i, et noté . C'est un objet à la base de la théorie des corps de classes.