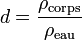Densité - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Histoire et terminologie - Densité des gaz - Expression de la densité - Densité et flottabilité - Densité pour les solides et les liquides - Densité et flottation des minerais métalliques - Densité des principaux métaux utilisés - Densité des liquides biologiques en médecine

Densité des gaz

La densité des gaz est calculée à partir de la densité de l'air. La valeur de référence prise est la masse d'un litre d'air à 0 °C sous une pression de 760 mmHg, soit 1,29349 g.

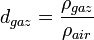
On a ainsi $d_{gaz}=\frac {\rho_{gaz}} {\rho_{air}}$

Il existe une façon commode de relier la masse molaire M d'un gaz et sa densité. En effet, en considérant un gaz parfait, $P V = n R T$ d'où :

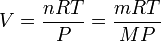
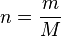
$V=\frac{nRT}{P}=\frac {mRT}{MP}$ avec $n=\frac {m}{M}$

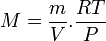
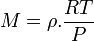
On a donc $M=\frac{m}{V}.{\frac{RT}{P}}$ ou $M=\rho.\frac{RT}{P}$

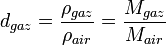
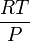
et $d_{gaz}=\frac{\rho_{gaz}}{\rho_{air}}=\frac{M_{gaz}}{M_{air}}$ avec $\frac{RT}{P}$ pris identique pour l'air et le gaz considéré.

En tenant compte de la composition de l'air et des masses molaires respectives (78% de diazote, 21% de dioxygène et 1% d'argon environ), il est facile de montrer que : $M a i r = 29 g . m o l - 1$ , soit $M g a z = 29. d$

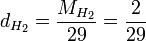
Par exemple, la densité du dihydrogène est $d_{H_{2}}=\frac {M_{H_{2}}}{29} = \frac {2}{29}$

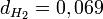
Soit $d_{H_{2}}=0,069$ environ.

Il découle de cette relation que plus un gaz a une masse molaire élevée, plus il est dense. Il est ainsi facile de prévoir que le dioxyde de carbone (CO₂) sera plus dense que l'air et que les gaz les moins denses sont le dihydrogène et l'hélium.

Le composé gazeux le plus dense à température ambiante est l'hexafluorure de soufre,SF₆.

Expression de la densité

La densité, notée d, s'exprime de la sorte :

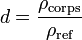
$d= \frac{\rho_{\rm corps}}{\rho_{\rm ref}}$

où $ρ corps$ est la masse volumique du corps considéré, et $ρ ref$ est la masse volumique du corps de référence.

Densité et flottabilité

Comparaison de deux corps avec densités supérieure et inférieure à un.

La densité peut indiquer la flottabilité d'un corps par rapport à l'eau douce. En effet, si la densité d'un corps est supérieure à 1 comme pour une vis métallique (voir illustration) le corps en question coule dans l'eau. À l'inverse, si la densité d'un corps est inférieure à 1 comme pour un bouchon de liège (voir illustration) le corps en question flotte sur l'eau. Dans l'eau de mer ou une solution saline à gradient de salinité, ces chiffres sont à ajuster.

Cas particulier de l'eau liquide

D'une manière générale quand un corps liquide refroidit sa densité augmente et devient maximale à la température de solidification. De plus le corps solide est généralement plus dense que le corps liquide. L'eau fait exception : sa densité maximale est atteinte non pas à 0 °C mais à 3,98 °C et la glace est moins dense que l'eau liquide. Cette particularité permet à l'eau tiède, à l'eau très froide et à la glace de flotter sur de l'eau à 3,98 °C. Si l'eau se comportait comme la plupart des autres corps, la glace tomberait au fond des lacs, des rivières et des océans, où la vie serait alors pratiquement impossible, du moins sous la forme que nous connaissons.

Parmi les métaux moins denses à l'état solide qu'à l'état liquide, il existe l'argent et le bismuth. Cela pose des problèmes importants lors du moulage, à cause du gonflement qui accompagne la solidification.

Densité pour les solides et les liquides

Le plus souvent, l'eau est utilisée comme corps de référence pour la densité des liquides et des solides. Dans ce cas, la masse volumique de l'eau est prise égale à 1 000 kg.m^-3 (ou à 1 kg.dm^-3, ou à 1 kg/L, ou encore 1 g/cm³). Il s'agit de la masse volumique de l'eau à 3,98 °C et à pression atmosphérique. En effet, l'eau possède une particularité parmi les liquides : sa densité et sa masse volumique sont maximales, non pas à sa température de fusion (0 °C) comme la plupart des liquides, mais à 3,98 °C. Or en métrologie, le fait de prendre comme référence une propriété physique qui passe par un extremum est très intéressant : au voisinage de cet extremum la propriété physique varie très peu. Ainsi au voisinage de 3,98 °C, une imprécision sur la détermination de la température exacte affecte très peu la masse volumique de l'eau et donc le résultat d'une mesure de densité.

La densité devient :

où $ρ corps$ est la masse volumique du corps considéré et $ρ eau$ est la masse volumique de l'eau (1000 kg/m³).

Pour corriger les valeurs mesurées à d'autres températures que la température de référence, il faut exploiter la courbe de variation de la masse volumique de l'eau en fonction de la température pour en déduire la masse volumique des matériaux à la température des mesures.

Histoire et terminologie

Densité et flottation des minerais métalliques