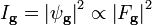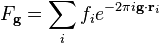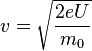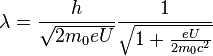Diffraction des électrons - Définition

Théorie

Interaction électronique avec la matière

Contrairement à d'autres types de radiation utilisés dans les études de diffraction sur des matériaux, comme les rayons X ou les neutrons, les électrons sont des particules chargés qui interagissent avec la matière par la force de Coulomb. Ceci signifie que les électrons incidents ressentent à la fois l'influence des noyaux atomiques positivement chargés et celle des électrons environnants. Pour comparaison, les rayons X interagissent avec la distribution spatiale des électrons de valence, alors que les neutrons sont diffusés par les noyaux atomiques par interaction forte. De plus, le moment magnétique des neutrons est non-nul, et ils sont parfois diffusés par les champs magnétiques. En raison de ces différentes formes d'interaction, les trois types de rayonnement sont pertinents pour différents types d'études.

Intensité des faisceaux diffractés

Dans l'approximation cinétique de la diffraction de l'électron, l'intensité d'un faisceau diffracté est donnée par :

Ici, est la fonction d'onde du faisceau diffracté et est le facteur de structure donné par :

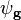
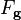
dans lequel est le vecteur de diffusion du faisceau diffracté, est la position d'un atome i dans la maille unitaire et f_i est le pouvoir de diffusion de l'atome, aussi appelé facteur de forme atomique. La somme est effectuée sur tous les atomes de la maille unitaire.

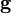
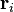
Le facteur de structure décrit la façon dont un faisceau incident d'électrons est diffusé par les atomes d'une maille unitaire cristalline, en prenant en compte les différents pouvoirs de diffusion des éléments grâce au terme f_i. Les atomes étant distribués dans le volume de la maille unitaire, il existe une différence de phase lorsque l'on considère l'amplitude diffusée entre deux atomes. Cette phase est prise en compte dans les termes exponentiels de l'équation.

Le facteur de forme atomique d'un élément dépend du type de radiation considéré. Les électrons interagissant avec la matière de manière différente des rayons X (par exemple), les facteurs de formes atomiques seront différents pour les deux cas.

Longueur d'onde des électrons

La longueur d'onde d'un électron est donnée par l'équation de De Broglie :

.

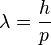
Ici h est la constante de Planck et p la quantité de mouvement de l'électron. Les électrons sont accélérés dans un potentiel électrique U jusqu'à atteindre la vitesse requise :

où m₀ est la masse de l'électron, et e la charge élémentaire. La longueur d'onde de l'électron est alors donnée par :

.

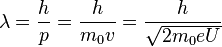
Ainsi, dans un microscope électronique, le potentiel d'accélération est habituellement de plusieurs milliers de volts, permettant à l'électron d'atteindre une proportion appréciable de la vitesse de la lumière. Un SEM peut ainsi fonctionner à des potentiels d'accélération typiquement de l'ordre de 10 000 volts (10 kV) donnant à l'électron une vitesse d'environ 20 % de celle de la lumière, alors qu'un TEM fonctionne vers 200 kV, portant l'électron à 70 % de la vitesse de la lumière. À ces vitesses, les effets relativistes doivent être pris en compte. On peut démontrer que la longueur d'onde des électrons est modifiée selon :

où c est la vitesse de la lumière. Le premier terme correspond au terme non-relativiste comme décrit plus haut, le second correspond au facteur relativiste. La longueur d'onde des électrons à 10 kV est donc de 12 3×10^-12 m (12,3 pm) alors que dans un TEM à 200 kV la longueur d'onde est de 2,5 pm. En comparaison, la longueur d'onde des rayons X utilisés en diffraction X est de l'ordre de 100 pm (Cu K_α : λ = 154 pm).