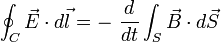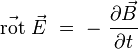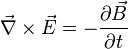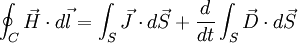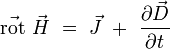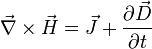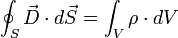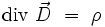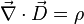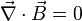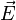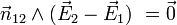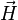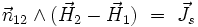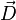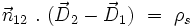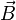Électrodynamique des milieux continus - Définition

Introduction

L'électrodynamique des milieux continus décrit les phénomènes électromagnétiques macroscopiques se déroulants au sein d'un milieu matériel, décrit comme un milieu continu.

L'hypothèse du milieu continu

Si l'on regarde la matière de « très près » (échelle nanoscopique), la matière est granulaire, faite d'atomes. Mais à l'œil nu (donc en se plaçant à notre échelle macroscopique), un objet solide ou fluide semble continu, c'est-à-dire que ses propriétés semblent varier progressivement, sans à-coups.

L'hypothèse des milieux continus consiste à considérer des milieux dont les propriétés caractéristiques qui nous intéressent — densité, élasticité, etc. — sont continues. Une telle hypothèse permet d'avoir recours aux outils mathématiques reposant sur les fonctions continues et/ou dérivables.

Des hypothèses supplémentaires peuvent éventuellement être faites ; ainsi un milieu continu peut être :

• linéaire
• homogène : ses propriétés sont les mêmes en tout point.
• isotrope : ses propriétés ne dépendent pas du repère dans lequel elles sont observées ou mesurées.
• parfait : le milieu se polarise ou s'aimante instantanément lorsqu'un champ extérieur est appliqué
• ohmique : lorsque le milieu est conducteur, la densité de courant qui le traverse est proportionnelle au champ électrique.

Lois fondamentales

En général, afin de décrire l'électrodynamique des milieux, l'on pose les 3 postulats fondamentaux suivants:

Équations de Maxwell macroscopiques

Quel que soit le milieu continu, les équations dites de Maxwell permettent de décrire l'évolution des grandeurs électromagnétiques dans ce milieu, et s'écrivent dans le système international des unités comme :

Loi	Forme "intégrale"	Forme "locale"
Loi d'induction de Faraday		ou
Loi de Maxwell-Ampère		ou
Loi de Gauss		ou
Absence de monopôles magnétiques		ou

Relations de passage

Les relations précédentes gouvernent l'évolution des grandeurs électromagnétiques dans chaque milieu continu, toutefois il est donc nécessaire d'y ajouter les règles qui décrivent le passage d'un milieu à l'autre :

Relation de passage	Forme "locale"
Continuité de la composante tangentielle de
Saut de la composante tangentielle de
Saut de la composante normale de
Continuité de la composante normale de

Où et ρ_s représentent respectivement le vecteur densité superficielle de courant, et la densité superficielle de charge, qui peuvent exister à l'interface séparant les deux milieux.

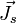
A noter que ces relations de passage ne sont pas indépendantes des équations de Maxwell, elles peuvent très bien en être déduites tout naturellement. Une démonstration rigoureuse existe au sens mathématique en utilisant la théorie des distributions de L. Schwarz, et en considérant que les équations de Maxwell sont vraies au sens des distributions. Cependant, pour des raisons pratiques, il est beaucoup plus commode de considérer séparément les équations de Maxwell prises au sens des fonctions, et les relations de passage.

Force exercée sur une charge

Voir l'article sur la Force électromagnétique ou Force de Lorentz. Dans un milieu continu, cela permet d'expliquer l'effet Hall ou la force de Laplace.