Fraction continue - Définition

Usages

Les usages des fractions continues sont innombrables. On trouvera par exemple dans Fraction continue et approximation diophantienne les preuves de l'irrationalité de e ou de π, dans Fraction continue d'un nombre quadratique un exemple de résolution d'équation de Pell-Fermat ou dans approximant de Padé un prolongement analytique de la série entière de la fonction tangente. Les usages donnés ici ne nécessitent pour leur compréhension que les propriétés décrites dans cet article.

Équation diophantienne linéaire

Claude-Gaspard Bachet de Méziriac a compris la relation entre les fractions continues et l'équation diophantienne linéaire.

L'équation diophantienne linéaire est l'équation suivante, où a, b et c sont des nombres entiers et où les solutions recherchées sont formées d'un couple d'entiers :

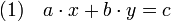
L'identité de Bézout indique que, si c est un multiple du plus grand commun diviseur de a et b, il existe toujours une solution. La fraction continue offre une méthode effective pour trouver toutes les solutions. Illustrons là par l'exemple 1245.x + 279.y = 6. Le développement en fraction continue de 1245/279 est égal à [4,2,6,7]. Calculons les différentes réduites, on trouve 4, 9/2, 58/13 puis 415/93. L'algorithme s'arrête, ce qui signifie que 415/93 est égal à 1245/279. En utilisant les coefficients de l'avant dernière réduite, on remarque que :

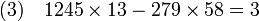
Dans cet exemple, 3 est le plus grand commun diviseur entre 1245 et 279. Ce résultat n'est pas le fruit du hasard, l'avant dernière réduite est toujours composée d'un couple solution de l'équation de Bézout et le résultat du dernier calcul est nécessairement le plus grand commun diviseur au signe près. En effet, notons h_j et k_j la j^ième réduite de la fraction a / b. Si n est l'indice de la dernière réduite, alors a / b est égal à h_n / k_n. Une des premières propriétés assure que :

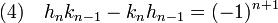
On en déduit qu'un diviseur commun à h_n et k_n divise le terme de gauche et donc le terme de droite de l'égalité (4), comme les seuls diviseurs de ±1 sont ±1, les deux termes h_n et k_n sont premiers entre eux. On en déduit que a = p.h_n et b = p.k_n et :

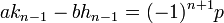
Cette solution démontre bien, au signe près, la propriété illustrée dans l'exemple (3). Il ne reste plus qu'à multiplier par 2 pour obtenir une solution :

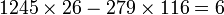
Les autres solutions s'obtiennent par adjonction d'une solution nulle. Une solution nulle est toujours de la forme (n.93, n.415) qui s'obtiennent comme les coefficients de la dernière réduite. On obtient finalement :

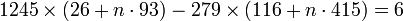
Automate planétaire

Christian Huygens construit un automate planétaire pour déterminer les positions relatives des corps célestes du système solaire.

Christian Huygens souhaite construire, à l'aide d'un mécanisme de type horlogerie un automate représentant le mouvement des planètes autour du soleil : « Ayant trouvè et fait exécuter depuis peu une machine automate qui représente les mouvements des Planètes dont la construction est d'une façon particulière et assez simple à raison de son effet, au reste d'une grande utilité à ceux qui étudient ou observent le cours des astres. ». La difficulté à laquelle il est confronté est liée au rapport de la durée d'une année terrestre et de celle de Saturne. En un an, la Terre tourne de 359° 45' 40'' 30''' et Saturne de 12° 13' 34'' 18'''. Le rapport est égal à 77 708 431/2 640 858. Combien faut-il de dents sur les deux engrenages supportant respectivement la Terre et Saturne ?

Huygens sait que les fractions continues offrent le meilleur compromis, ce qu'il exprime ainsi : « Or, lorsqu’on néglige à partir d’une fraction quelconque les derniers termes de la série et celles qui la suivent, et qu’on réduit les autres plus le nombre entier à un commun dénominateur, le rapport de ce dernier au numérateur sera voisin de celui du plus petit nombre donné au plus grand; et la différence sera si faible qu’il serait impossible d’obtenir un meilleur accord avec des nombres plus petits. ».

Un calcul en fraction continue montre que :

On obtient la suite de fractions : 29/1, 59/2, 147/5, 206/7, 1 177/40 ... Les deux premières solutions ne sont guère précises, dans le premier cas, à la fin d'une rotation de Saturne, la position de la terre est fausse à près d'un demi-tour, dans l'autre cas l'erreur dépasse 4°. La cinquième est techniquement difficile, elle demande la fabrication d'une roue à plus de 1 000 dents ou plusieurs roues. La quatrième offre une précision proche de 3/1 000. C'est celle que choisit Huygens.

Si la terre fait cents tours complets, sur l'automate planétaire Saturne en fait 700/206, soit trois tours et un angle de 143° 18'. Dans la réalité, Saturne a tourné de 143° 26'. Soit une erreur de 8 minutes d'angle, largement inférieure aux imprécisions mécaniques de l'horloge. Un calcul analogue montre que la fraction 147/5 donne, dans le même contexte, une erreur supérieure à un degré, pour une mise en œuvre d'une difficulté technique comparable.