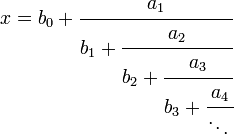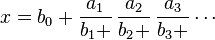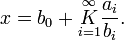Fraction continue - Définition
La liste des auteurs de cet article est disponible ici.
Fraction continue généralisée
Notations
Une fraction continue généralisée est une généralisation des fractions continues où les numérateurs et dénominateurs partiels peuvent être des réels ou complexes quelconques :
où an (n > 0) sont les numérateurs partiels et les bn les dénominateurs partiels, en particulier le coefficient b0 est appelé la partie entière de la fraction.
Des notations plus compactes sont employées :
Alfred Pringsheim les écrivait comme suit :
-
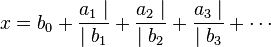
Karl Friedrich Gauss utilisa une notation rappelant la notation Σ des séries ou Π du produit infini:
où la lettre K est l'initiale de Kettenbrüche, signifiant "fraction continue" en allemand. Cette notation suggère cependant des simplifications de diviseurs communs aux numérateurs et dénominateurs partiels, qui modifient la fraction continue.
Équation du second degré

Un exemple d'illustration de l'arrivée naturelle d'une fraction continue généralisée est l'équation du second degré. Étudions le cas particulier, correspondant celle de Bombelli, la première connue en Europe :
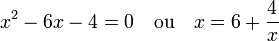
En remplaçant x par sa valeur, on obtient, comme valeur de x :
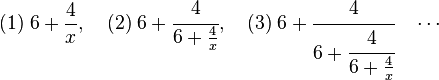
En notation de Pringsheim, la fraction f prend la forme suivante :
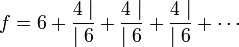
Cette fois ci, aucun théorème n'indique la convergence a priori d'une fraction continue de cette nature. Un calcul manuel montre que les premières réduites sont 2, 9/2, 28/9, 101/8, 342/101. On vérifie bien que cette suite tend vers une des deux racines, ici celle égale à 3 + √13. D'une manière générale, si l'équation admet au moins une racine réelle et si le coefficient de x dans l'équation du second degré n'est pas nul, cette fraction continue généralisée tend vers la racine de plus grande valeur absolue. En revanche, dans les autres cas, la fraction continue n'est pas convergente, ainsi aucun théorème ne peut garantir la convergence d'une fraction continue quelconque. Ce résultat est l'œuvre d'Euler. À l'époque de Bombelli, l'intérêt principal de cette fraction continue était d'offrir une méthode d'extraction de racine, le calcul de la fraction permet d'approcher √13 avec toute la précision souhaitée.
Étudions le cas général de l'équation du second degré :
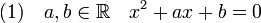
Si le cas semble ne pas tout à fait être général car le coefficient dominant, celui de x2 est égal à 1, il est possible de remarquer qu'en divisant par ce coefficient l'équation du second degré, on revient à la situation étudiée.
La méthode proposée ici est générale pour l'étude de la convergence d'une fraction continue généralisée. Les relations de récurrences deviennent, si on ajoute un indice -1 :
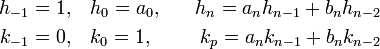
Ici (an) désigne la suite des coefficients des dénominateurs, correspondant au cas de la fraction continue simple et (bn) à celle des coefficients des numérateurs, égaux à 1 dans le cas d'un fraction simple.
Il devient possible d'écrire les relations de récurrence de manière matricielle. Si Hn désigne la matrice colonne de coordonnées hn et hn-1 et Kn son équivalent pour le dénominateur, la relation de récurrence s'écrit aussi :
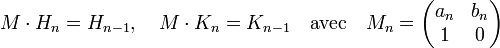
La question, dans le cas général, revient à une multiplication de matrice 2x2. Si Nn désigne la matrice produit des Mj pour j plus petit ou égal à n, on obtient :
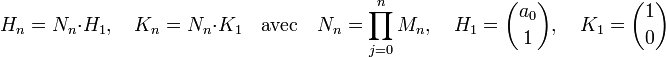
Pour le cas particulier de l'équation qui nous intéresse, le problème n'est pas si complexe car an est égal à -a et bn à -b, et on remarque que kn est égal à hn-1. La matrice Mn est ainsi indépendante de n et la résolution de la question revient à calculer les puissances d'une matrice 2x2. Une autre manière de voir les choses est de remarquer que la relation de récurrence est linéaire et d'appliquer directement les résultats. L'objectif de la suite de la démonstration est l'illustration d'un cas simple d'un produit de n matrices 2x2, configuration fréquente dans le cas de l'étude d'une fraction continue.
La méthode la plus simple de résolution est, si possible, de diagonaliser M, ce qui revient à écrire que M est égal à P.D.P -1 où D désigne une matrice diagonale et P une matrice de passage. La matrice Nn est égale à P.D n.P -1. Pour cela, il est nécessaire de trouver les valeurs propres δ1 et δ2 de la matrice M, qui correspondent aux racines du polynôme caractéristique, qui se trouve être celui de l'équation (1). Deux cas se présentent :
-
- Les racines de l'équation (1) sont distinctes (complexes ou réelles) :
Si les valeurs propres sont distinctes, il existe deux vecteurs propres libres, qui forment une base. La matrice Dn est diagonale de valeurs propres δ1n et δ2n. L'expression de hn est nécessairement une combinaison linéaire des deux valeurs propres de la matrice Dn, ce qui montre l'existence de deux coefficients non nuls λ et μ tel que :
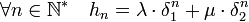
Les deux coefficients ne peuvent être nuls, pour s'en rendre compte, il suffit de remarquer que K1 n'est pas un vecteur propre, on en déduit que Kn-1 et Kn ne le sont pas non plus, or si l'un des coefficients était nul les deux vecteurs colonnes Kn-1 et Kn sertaient proportionnels, ce qui ne peut arriver que dans le cas d'un vecteur propre. Pour calculer la ne réduite, il suffit de remarquer que kn est égal à hn-1. On désigne par δ1 la plus grande des deux racines en valeur absolue si elles sont réelles et en module, si elles sont imaginaires. Si a et b ne sont pas tous les deux nuls (le cas a et b tous deux nuls n'a pas d'intérêt ici), δ1 est nécessairement différent de 0, car les racines sont supposées distinctes et ne peuvent être toutes les deux nulles, ce qui permet d'écrire :
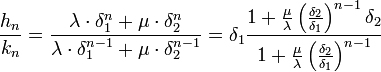
Ce cas se divise alors en deux :
-
-
- Le coefficient b n'est pas nul et les racines sont réelles :
-
Dans ce cas, δ1 est en valeur absolue strictement supérieur à δ2 et leur quotient à la puissance n - 1 tend vers 0, la réduite d'indice n converge vers δ1.
-
-
- Le coefficient b est nul ou les racines sont imaginaires :
-
Si b est nul δ1 et δ2 sont de signes opposés, si les racines sont imaginaires elles sont conjuguées et de même module leur rapport est dans les deux cas une valeur ω qui est un nombre complexe de module 1. La valeur ωn-1 tourne dans le cercle unité et ne converge pas, La réduite d'indice n n'est donc pas convergente.
-
- Les racines de l'équation (1) sont doubles :
Notons δ la racine. Une diagonalisation est impossible, mais la réduction de Jordan montre que la matrice est somme d'une matrice d'homothétie H de rapport δ et d'une matrice nilpotente R constituée uniquement de 0 sauf pour le coefficient en haut à droite, égal à 1. Comme la matrice H est celle d'une homothétie, elle commute avec R et il est possible d'appliquer la formule du binôme, ce qui donne, en remarquant que toutes les puissances Rj sont nuls si j > 1 :
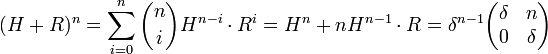
On en déduit encore l'existence de deux coefficients λ et μ tel que :
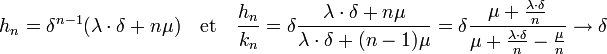
Et, si n croît indéfiniment, la fraction réduite d'indice n tend vers l'unique racine.
Fraction continue de π et de e

Un calcul, dans la partie introductive de l'article, montre comment déterminer la fraction continue de π. Néanmoins, chaque étape est plus pénible car elle demande une précision sur la valeur initiale de plus en plus grande. Les séries entières, convergeant vers π, offrent bien une solution théorique pour le calcul de chaque coefficient de la fraction continue, mais il est calculatoirement trop inextricable pour être utilisable. Pour cette raison, il est plus simple d'obtenir une expression en fraction continue généralisée. La suivante est l'œuvre de Brouncker :
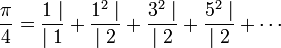
La démonstration se trouve dans l'article Fraction continue et approximation diophantienne.
Pour obtenir celle de e, on utilise un développement en fraction continue, non pas d'un nombre mais d'une fonction, plus précisément celle de l'exponentielle :
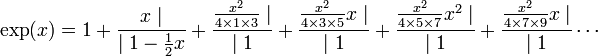
Sa construction se trouve dans l'article Approximant de Padé de la fonction exponentielle. Ainsi, une fraction continue ne s'applique pas uniquement aux nombres, mais aussi à certaines fonctions. Le développement de π/4 présentée ici, peut être vu comme une fraction continue d'approximants de Padé de la série entière de la fonction Arctangente.