Fraction continue - Définition
La liste des auteurs de cet article est disponible ici.
Approche intuitive
De l’algorithme d’Euclide aux fractions continues
On commence par rappeler le déroulement de l'algorithme dû à Euclide de recherche du PGCD, en analysant l'exemple des deux nombres entiers 15 625 et 6 842. On procède à une suite de divisions euclidiennes avec reste :
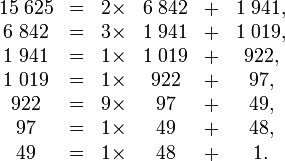
Une autre manière d'interpréter cet algorithme consiste à approcher par étapes le quotient 15 625 / 6 842. La partie entière de ce quotient est 2, ce qui permet d'écrire
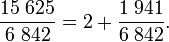
Que peut-on dire de la fraction 1 941 /6 842, à part qu'elle est plus petite que 1? Elle est comprise entre 1/4 et 1/3, son inverse, 6 842 / 1 941, possède une partie entière est 3 ; et plus précisément, si l'on utilise les résultats de la deuxième division euclidienne :
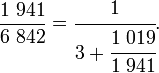
Ainsi de proche en proche :
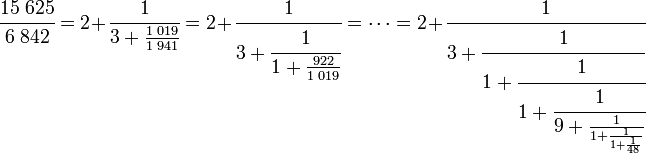
qui est bien une fraction continue. On utilise parfois la notation suivante, plus commode :
![\frac{15\;625}{6\;842}=[2,3,1,1,9,1,1,48].](https://static.techno-science.net/illustration/Definitions/autres/5/57f65fed6ac3be83b32cbf4f81bf0220_da81887f3a2ce6f9721e5779d456c3c4.png)
On peut comparer 15 625 / 6 842 à ses approximants obtenus en tronquant successivement le nombre d'étages de la fraction continue. Le tableau suivant donne les troncatures en notation fractionnelle puis décimale, et la différence entre l'approximant et le nombre 15 625 / 6 842.
| Fraction | Développement décimal | Erreur |
|---|---|---|
| 2 | 2,0000... | -0,283 688 979 83... |
| 7/3 = 2 + 1/3 | 2,333... | 0,049 644 353 5... |
| 9/4 = 2 + 1/(3 + 1/1) | 2,250 0... | -0,033 688 897 983... |
| 16/7 | 2,285 714 285 714 2... | 0,002 025 305 88... |
| 153/67 | 2,283 582 089 55... | -0,000 106 890 28... |
| 169/74 | 2,283 783 783 7...... | 0,000 094 803 95... |
| 322/141 | 2,283 687 943 2 | -0,000 001 036 57... |
| 15 625/6 842 | 2,283 688 979 83... | 0 |
La suite des erreurs est décroissante en valeur absolue et de signes alternés.
Développement en fraction continue d'un rationnel
On peut chercher si tout nombre rationnel r admet un développement en fraction continue. Soit donc r = p / q une de ses représentations fractionnaires. On cherche, s'il existe, un nombre positif ou nul n, un entier relatif a0 et des entiers strictement positifs aj pour j ≥ 1, tels que r = [a0, ...,an]. Sans perte de généralité, on peut supposer q > 0, et introduire les nombres p0, p1,... et a0, a1, ... comme suit.
On pose p0 = p , p1 = q
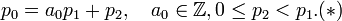
C'est une division euclidienne ordinaire si p0 est positif ou nul. S'il est strictement négatif, on a -p0 = a'0.p1 + p'2 avec a'0 entier positif ou nul, 0 ≤ p'2 < p1. Si p'2 est nul, on pose a0 = a'0 et p2 = 0, et s'il n'est pas nul, on pose a0 = -a'0 - 1 et p2 = p1 - p'2. Dans ces deux cas, on obtient encore (*). Tant que pj n'est pas nul, on pose
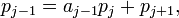
avec aj-1 entier au moins égal à 1(pour j >1) et 0 ≤ pj+1 < pj. On note n le plus grand entier pour lequel pn+1 n'est pas nul. On sait donc que pn+1/pn est un entier supérieur à 1. On a alors
![\frac{p_0}{p_1}=[a_0,p_1/p_2]=[a_0,a_1,p_2/p_3]=\dots=[a_0,a_1,\dots,a_n].](https://static.techno-science.net/illustration/Definitions/autres/5/5db463ebd6c76f090b503e8a2b9baca7_a80b2b1cfc462ab42e3d8e3411a8ee9d.png)
On peut vérifier que :
![[a_n]=p_n/p_{n+1},\quad [a_{n-1},a_n]=a_{n-1}+p_{n+1}/p_n=p_{n-1}/p_n,[a_j,\dots,a_n]=a_j+p_{j+2}/p_{j+1}=p_j/p_{j+1}](https://static.techno-science.net/illustration/Definitions/autres/1/1cdc6258095bc4dfd7f03ae4e843862a_863634f3aab5159b9f5e0229a0afe21a.png)
et une récurrence immédiate montre [a0, ...,an] = p / q.
On a donc montré que l'algorithme du PGCD d'Euclide fournit systématiquement un développement en fraction continue d'un nombre rationnel. Le développement ainsi obtenu est toujours fini.
Les numérateurs et dénominateurs des différentes réduites s'obtiennent par l'algorithme d'Euclide étendu.
On peut se demander s'il y a d'autres développements finis d'un rationnel en fraction continue. On remarque d'abord que pour tout entier relatif m, [m-1, 1] est identique à m. Par conséquent, si r admet le développement en fraction continue [a0, ..., an] avec an > 1 , il admet aussi le développement [a0, ..., an - 1, 1]. Un raisonnement simple par récurrence montre qu'il ne peut y avoir d'autres développements en fraction continue que ceux qui viennent d'être donnés. Enfin, on peut montrer que tout rationnel possède un développement en fraction continue fini.
On sait déjà que si x possède un développement fini en fraction continue, il est rationnel.
Réciproquement montrons que si x est rationnel, il admet un développement fini en fraction continue. Soit p et q deux entiers tels que x soit égal à p / q. Ici q désigne un entier strictement positif. Montrons par récurrence sur q que x admet une représentation finie.
Si q est égal à 1, alors x est égal à p, ce qui fournit une représentation en fraction rationnelle finie.
Supposons la propriété vérifiée pour toutes les fractions admettant un dénominateur strictement plus petit que q. La division euclidienne de p par q montre l'existence de deux entiers d et r tels que :
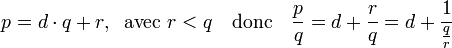
L'hypothèse de récurrence montre que la fraction q / r admet un développement fini en fraction continue. Le remplacement de la valeur q / r dans l'expression précédente fournit un développement fini en fraction continue de p/q ce qui termine la démonstration.
Développement en fraction continue du nombre π
Une remarque permet de généraliser la méthode précédente à un nombre réel quelconque. Pour l'illustrer, appliquons-la sur le nombre π. La première étape, dans le cas d'un rationnel, était le calcul de la division euclidienne du numérateur par le dénominateur, ce qui ne fait plus sens pour un réel, en revanche le résultat est égal à la partie entière de la fraction, qui possède toujours un sens. La partie fractionnaire, nécessairement plus petite que 1, était inversée, ce qui est encore possible ici. On obtient :
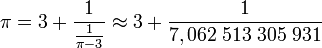
Comme π est irrationnel, l'inverse de π - 3 l'est encore, l'algorithme ne s'arrête pas. Comme π - 3 est plus petit que 1, c'est une partie fractionnaire, son inverse est plus grand que 1 et l'on peut appliquer la même démarche :
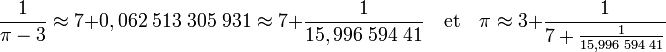
Le nouvelle valeur approximativement égale à 15,997 est encore un irrationnel strictement supérieur à 1, d'où la possibilité d'une nouvelle étape, puis d'une nouvelle :
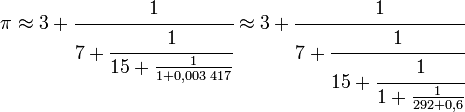
On comprend que le processus ne s'arrête jamais, si le calcul est réalisé avec un nombre de décimales suffisant. On obtient comme suite de fractions 3 puis 22/7 ≈ 3,1428 puis 333/106 ≈ 3,14150 puis 355/113 ≈ 3,1415929 et enfin 103 993 / 331 02 proche de π avec une précision meilleure que le milliardième. Une fois encore, la suite des erreurs est décroissante en valeur absolue et de signes alternés.
Représentation géométrique
L'algorithme d'Euclide permet de calculer une fraction continue dans le cas des nombres rationnels. Cet algorithme admet dans ce cadre une interprétation géométrique. Soit r = p / q un nombre rationnel, on considère un rectangle de longueur p et de largeur q, et on le pave par des carrés de côté q.
Si x est un nombre entier, le pavage comporte exactement x carrés. Sinon, soit a0 le nombre de carrés insérés dans le rectangle, ou encore, le premier terme de la fraction continue. Il reste une bande non pavée de dimension q x b1 avec b1 égal à p - a0.q ; on pave cette bande avec des carrés de dimension maximale, c'est-à-dire de côté x1. Le nombre de carrés est égal au deuxième terme a1 de la fraction continue. En réitérant la méthode, on obtient l'intégralité des coefficients ap.
Dans l'image ci-contre, on pave le rectangle 30 x 13 par deux carrés de côtés 13. Il reste une bande de longueur 13 et de largeur 4. En termes de fraction continue, on obtient l'égalité :
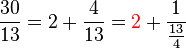

Ensuite, on remarque qu'il est possible de remplir la bande restante de 3 carrés de côté 4 et il reste une bande de longueur 4 et de largeur 1. Ce qui permet de terminer le calcul de la fraction continue :
![13 = 3\times4 + 1 \;\Rightarrow \; \frac {30}{13} = {\color{Red}2} + \frac 1{\frac {3\times 4 + 1 }4} = {\color{Red}2} + \frac 1{{\color{Red}3} + \frac 1{\color{Red}4}}= [2,3,4]\;](https://static.techno-science.net/illustration/Definitions/autres/d/d3a978cf1f9ec4fcc4521d8c7ab200c8_8cf874554bde2a4637ecdedbe61177a2.png)
La même construction permet de trouver le rationnel dont on connait le développement en fraction continue. Dans l'image de gauche on peut retrouver le rationnel dont le développement est [1, 1, 2, 3]. Le dernier coefficient est égal à 3, on trouve donc 3 petits carrés de côté 1, qui donnent la taille du carré suivant (3). L'avant dernier coefficient 2 indique qu'il existe deux carrés moyens de côté 3. Ces deux côtés et le petit carré donnent la taille du carré plus grand (7). Le coefficient associé est égal à 1, il n'en n'existe donc qu'un unique de cette nature. Le carré plus grand (7) et le carré moyen (3) donnent le côté du dernier carré (10). Les deux derniers carrés donnent la longueur totale du rectangle (17). La fraction recherchée est égale à 17/10.
Le processus s'arrête car p et q sont commensurables c'est-à-dire qu'il existe une longueur l et deux entiers a et b tels que p = l.a et q = l.b.
Considérons maintenant un rectangle de longueur L et de largeur l. Si le quotient L / l n'est pas rationnel, c'est-à-dire si les longueurs L et l sont incommensurables, le processus ne s'arrête pas.
Tel est le cas pour la figure de droite représentant un rectangle d'or, c'est-à-dire un rectangle dont le rapport de la longueur sur la largeur est égal à φ le nombre d'or. On ne peut placer qu'un carré dans chaque bande ce qui amène à la représentation :
![\varphi = [1 , 1 , 1 , \cdots]](https://static.techno-science.net/illustration/Definitions/autres/6/6491b9da3aff9745da4e8d087553dfea_92ec154f042ec6179aaff803355c2fec.png)
La suite des numérateurs, ainsi que celle des dénominateurs sont de Fibonacci.
Repère chronologique
L'usage des fractions continues est ancien. Âryabhata , un mathématicien indien les utilise pour résoudre des équations diophantiennes ainsi que pour approximer précisément des nombres irrationnels. Brahmagupta étudie plus en profondeur l'équation maintenant dite de Pell-Fermat. Il développe les premiers fondements de la méthode chakravala, usant de calculs proches de ceux des fractions continues. Il cherche à résoudre l'équation x2 - 61. y2 = 1 et trouve la plus petite solution :
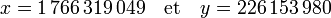
Au XIIe siècle, la méthode est enrichie par Bhāskara II. Un algorithme, analogue à celui des fractions continues, permet de résoudre un cas général. La différence la plus marquante est qu'il autorise les nombres négatifs dans la fraction, permettant une convergence plus rapide.
L'apparition en Europe est plus tardive et italienne. Rafael Bombelli fait usage d'un ancêtre des fractions continues pour le calcul d'approximations de la racine carrée de 13. Pietro Antonio Cataldi comprend que la méthode de Bombelli s'applique pour toutes les racines carrées, il l'utilise pour la valeur 18 et écrit un petit opuscule à ce sujet. Il remarque que les approximations obtenues sont alternativement supérieures et inférieures à la racine carrée cherchée.

Un progrès décisif a lieu en Angleterre. Le 3 janvier 1657, Pierre de Fermat défie les mathématiciens européens avec plusieurs questions dont l'équation déjà résolue par Brahmagupta. Piqué au vif, la réaction anglaise est rapide. William Brouncker trouve la relation entre l'équation et la fraction continue, ainsi qu'une méthode algorithmique équivalente à celle des indiens pour le calcul de la solution. Il utilise la fraction continue pour construire une suite convergente vers 4/π, et approxime π avec dix décimales significatives. Ces résultats sont publiés par John Wallis qui en profite pour démontrer les relations de récurrence utilisées par Brouncker et Bhāskara II. Il donne le nom de fraction continue dans la phrase : « Nempe si unitati adjungatur fractio, quae denominatorem habeat continue fractum. ». À cette époque, Christian Huygens découvre que les fractions continues sont l'outil idéal pour déterminer le nombre de dents que doivent contenir les roues des engrenages dans l'horlogerie. Il l'utilise pour la mise au point d'un automate planétaire.
Quelques questions théoriques sont résolues au siècle suivant. L'usage montre que l'algorithme des fractions continues permet de résoudre l'équation de Pell-Fermat en utilisant le fait que la fraction est périodique à partir d'un certain rang. Leonhard Euler montre que si un nombre possède une fraction continue périodique, alors il est solution d'une équation du second degré à coefficients entiers. La réciproque, plus subtile est l'œuvre de Joseph-Louis Lagrange . Durant ce siècle, Johann Heinrich Lambert trouve une nouvelle utilité aux fractions continues. Il les utilise pour montrer l'irrationalité de π.
Cet usage devient fréquent au XIXe siècle. Evariste Galois trouve la condition nécessaire et suffisante pour qu'une fraction continue soit immédiatement périodique. Joseph Liouville utilise le développement en fraction continue généralisée pour exhiber des nombres non algébriques, c’est-à-dire transcendants. Ce sont les nombres de Liouville. En utilisant les fractions continues, Charles Hermite prouve la transcendance de e, base du logarithme népérien en 1873. Grâce à lui, Ferdinand von Lindemann prouve en 1882 que π est transcendant et démontre par la même que la quadrature du cercle est impossible à réaliser. À la fin du siècle Henri Padé développe la théorie des approximants qui portent maintenant son nom et qui sont des fractions continues de polynômes. Cette technique est utilisée par Henri Poincaré pour démontrer la statibilité du système solaire. Georg Cantor prouve que les points d'un segment et ceux situés à l'intérieur d'un carré sont en bijection à l'aide des fractions continues. Les fonctions de cette nature sont étudiées dans le cadre de la théorie du chaos, elles sont discontinues sur chaque point rationnel de l'intervalle [0,1].




















































