Fraction continue - Définition
La liste des auteurs de cet article est disponible ici.
Approche théorique
Algorithme de développement en fraction continue pour un réel
Dans l'algorithme d'Euclide développé précédemment, l'entier aj, quotient de pj dans la division euclidienne par pj+1 est aussi la partie entière du réel xj défini par pj/pj+1. Le réel pj+2/pj+1 représente la partie décimale de xj et peut encore s'écrire xj - aj. Le réel xj+1 défini par pj+1/pj+2 correspond donc à 1/(xj - aj).
À l'aide des idées introduites précédemment, on peut alors définir un développement en fraction continue pour tout réel x . Le symbole
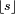
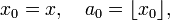
ainsi que la définition récurrente, tant que xj n'est pas entier,
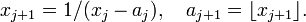
L'entier n désigne, s'il existe, le premier indice pour lequel xj est entier, on définit alors an comme étant égal à xn. Le développement obtenu par le présent algorithme est alors fini. Sinon, il ne s'arrête jamais.
On peut formaliser de manière plus informatique cet algorithme :
- Donnée : un nombre x réel.
- Initialisation : on assigne la valeur x à la variable X. La suite a est vide.
- Boucle: On assigne à la variable A le plus grand entier au plus égal à X, on concatène cette valeur à la suite a. Si X est entier, l'algorithme s'arrête. Si X n'est pas entier, on assigne à X la valeur de 1 /(X - A) et on recommence au début de la boucle.
On sait que cet algorithme s'arrête si et seulement si x est rationnel.
Notations et terminologie
Pour des nombres aj, j ≥ 0, qu'on peut aussi voir comme des variables formelles, on introduit les expressions suivantes:
![[a_0]=a_0,\quad [a_0,a_1]=a_0+\frac{1}{a_1},\quad \dots [a_0,\dots,a_j] =a_0+\frac{1}{[a_1,\dots,a_j]},](https://static.techno-science.net/illustration/Definitions/autres/c/c8108c19a138b1b596f23e09a7b9e16a_1c92cc44a4e4c6dbbceabee5dc19224c.png)
quel que soit l'entier positif j. Si a0 est un entier relatif, et si a1,... , ap sont des entiers strictement positifs, l'expression [a0,... , ap] est bien définie et fournit un nombre rationnel.
Si x est un nombre réel, il est possible de définir les suites (aj) et (xj) à l'aide de la méthode du paragraphe précédent.
-
- La suite (ap) est appelée fraction continue ou fraction continue simple du réel x.
Si x est rationnel, la suite s'arrête pour un indice n, sinon elle est infinie.
L'usage des deux mots dépend du contexte. Dans certains cas, la majorité des expressions sont du type étudié jusqu'à présent. Pour plus de simplicité on parle de fraction continue. Les expressions différentes, par exemple parce que an devient négatif ou réel quelconque, sont appelées fractions continues généralisées. Dans d'autres situations, l'expression générale n'est pas celle où an est un entier, il peut être par exemple, une fonction complexe ou une matrice, le terme de fraction continue désigne alors l'objet mathématique principal étudié et les fractions dont il est question ici prennent le nom de fraction continue simple.
-
- Le terme ap est appelé coefficient d'indice p.
-
- La fraction [a0, a1, a2, ..., ap] est appelée réduite ou encore quotient incomplet d'indice p.
-
- Le terme xp est appelé quotient complet d'indice p.
Deux notations sont fréquemment utilisées dans ce contexte :
![x = a_0 + \cfrac 1{a_1 + \cfrac 1{a_2 + \frac 1{\cdots}}} = [a_0, a_1, a_2, \cdots]](https://static.techno-science.net/illustration/Definitions/autres/1/1a2a14c315f1e0936159856dc088155e_9d656ca7cc89b7d9d6b0e36d6523cf16.png)
Ces notations seraient abusives si la suite des réduites n'étaient pas convergente vers x, ce qui n'a été vérifié que pour les rationnels. Le reste de l'article montre que cette convergence existe toujours, ce qui justifie la notation.
Réduites d'une fraction continue
Dans le reste de la section, x est un réel, (ap) sa fraction continue et (xp) la suite associée à x selon les notations du premier paragraphe de la section. La lettre n désigne l'indice du dernier terme de la suite (ap) si x est rationnel, et désigne l'infini si x est irrationnel. Enfin p désigne un entier positif ou nul, inférieur ou égal à n.
Par définition de la fraction continue, on dispose de l'égalité :
![x = [a_0, a_1, \cdots, a_{p-1}, x_p]](https://static.techno-science.net/illustration/Definitions/autres/4/4bad23c6c017597da51b4871d49341cb_2a29bf14f360663a26b8d4ac97b6d3dc.png)
-
- Si p est strictement positif alors xp est un réel supérieur à 1, et ap est un entier strictement positif.
Ceci provient de la définition de xp comme inverse de partie fractionnaire d'un nombre, et de la définition de ap comme partie entière de xp.
-
- Si un nombre réel strictement positif x admet un développement en fraction continue de la forme [a0,a1,...], alors, son inverse 1/x admet pour développement en fraction continue [a1,a2,...] dans le cas où a0 est nul, et [0,a0,a1,...] dans les autres cas.
Soit (hp) et (kp) les suites d'entiers (qui sont strictement positifs à partir du rang 1), définies par récurrence par : .
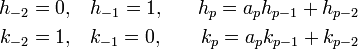
Alors on a les trois propriétés suivantes :
-
- Pour tout
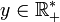
- Pour tout
![\quad \left[a_0, a_1, \,\dots, a_{p-1}, y \right]= \frac{y h_{p-1}+h_{p-2}} {y k_{p-1}+k_{p-2}}](https://static.techno-science.net/illustration/Definitions/autres/a/a5e5cfafaadbfbba9fc495d488291d40_d6b73ce4c230b37847b791c162914367.png)
-
- L'égalité suivante est vérifiée :
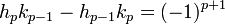
-
- L'écriture irréductible de la réduite d'ordre p est
![[a_0,a_1,\cdots a_p]=\frac{h_p}{k_p}](https://static.techno-science.net/illustration/Definitions/autres/b/b3f1d3c7a6990f3243bbf3ddf2752322_54f1781e3bc1d85770e40e383c2663c1.png)
Irréductible signifie que le numérateur et le dénominateur sont deux entiers premiers entre eux.
Si les coefficients de la fraction continue sont tous égaux à 1 - ce qui est le cas dans le développement en fractions continues du nombre d'or - les entiers hp et kp vérifient la relation de récurrence de Fibonacci, ce sont des nombres de Fibonacci consécutifs, ce qui explique que les quotients de deux termes consécutifs de la suite de Fibonacci donnent des approximations de plus en plus fines du nombre d'or.
-
- Pour tout
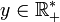
- Pour tout
![\quad \left[a_0, a_1, \,\dots, a_{p-1}, y \right]= \frac{y h_{p-1}+h_{p-2}} {y k_{p-1}+k_{p-2}}](https://static.techno-science.net/illustration/Definitions/autres/a/a5e5cfafaadbfbba9fc495d488291d40_d6b73ce4c230b37847b791c162914367.png)
Montrons cette propriété par récurrence sur p.
Lorsque p est nul les deux membres de l'identité valent y : elle est donc vérifiée.
Soit p un entier positif ou nul ; supposons la propriété vraie à l'ordre p . Elle est en particulier vraie lorsque y prend la valeur ap + 1/y, ce qui permet d'écrire :
![\begin{array} {rl}[a_0,\cdots, a_p, y] &= [a_0,\cdots, a_{p-1}, a_p + \frac 1y]\\ & = \frac {(a_p + \frac 1y)h_{p-1} + h_{p-2}}{(a_p + \frac 1y)k_{p-1} + k_{p-2}}\\ & = \frac {y(a_ph_{p-1} + h_{p-2}) + h_{p-1}}{y(a_pk_{p-1} + k_{p-2}) + k_{p-1}}\\ & =\frac{y h_{p}+h_{p-1}} {y k_{p}+k_{p-1}} \end{array}](https://static.techno-science.net/illustration/Definitions/autres/4/49274dd04a874e45af5c4582f4c3d365_55d5b989982e3c244b38fd955ad33ad9.png)
-
- En posant y = ap, dans l'égalité précédente, on peut écrire
![\begin{array} {rl}[a_0,\cdots, a_{p-1}, a_p] &= \frac{a_p h_{p-1}+h_{p-2}} {a_p k_{p-1}+k_{p-1}}\\ & =\frac{h_p}{k_p} \end{array}](https://static.techno-science.net/illustration/Definitions/autres/7/725bbebe39aec8aa81f8567d5fa3249c_202ab19d7b90da951fcc0b42f72665a0.png)
-
- L'égalité suivante est vérifiée :
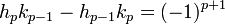
Montrons cette égalité par récurrence sur p.
Lorsque p est nul les deux membres de l'égalité valent -1 ; elle est donc vérifiée.
Soit p un entier positif ou nul ; supposons vérifiée cette égalité à l'ordre p et vérifions la à l'ordre p+1. On calcule alors :
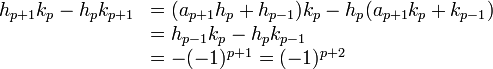
La dernière égalité prouve que les entiers hp et kp sont premiers entre eux et que l'écriture de la réduite est bien une fraction irréductible.
Encadrement et convergence
La valeur x désigne maintenant un nombre irrationnel strictement positif. La suite (ap) est infinie et ne prend que des valeurs positives.
-
- Les deux suites (hp) et (kp) sont strictement croissantes et ont pour limite l'infini.
En effet, cette proposition est la conséquence directe de la relation de récurrence établie au paragraphe précédent. Une récurrence montre que la valeur de kp est au moins égale à 2p/2.
La suite des réduites est convergente, quelques propositions montrent la nature de cette convergence :
-
- La différence entre deux réduites successives est :
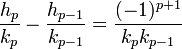
-
- Les réduites de rangs pairs et impairs sont respectivement croissante et décroissante et définissent deux suites adjacentes convergeant vers x .
Ce résultat s'exprime aussi sous la forme suivante :
-
- La valeur x est la limite de la série alternée :
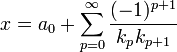
Si (ap) est une suite d'entiers strictement positifs et (sp) la réduite[a0, ...,ap] est la pième somme partielle de la série précédente qui est convergente. Si x désigne la limite de la série, alors la fraction continue de x est donnée par [a0, ...,ap, ...]. Ainsi, toute suite d'entiers strictement positifs, sauf peut être le premier, correspond au développement en fraction continue d'un réel.
La différence entre x et une réduite est évaluée par les formules suivantes :
-
- Pour tout entier p, la différence entre la valeur x et la réduite d'indice p est donnée par la formule suivante, si xp+1 désigne le quotient complet d'indice p + 1 :
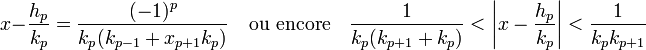
Ce qui montre que la limite d'une fraction continue est bien la valeur du nombre x initial. De plus, deux fractions continues de même limite ont nécessairement les mêmes coefficients. Soit en effet deux fractions continues ayant même limite x, montrons par récurrence que leur p premiers coefficients sont égaux. Si a0 et la partie entière de x alors les deux fractions continues ont pour premier coefficient a0. Supposons la propriété démontrée pour les p premiers coefficients. Le même raisonnement montre qu'ils ont même quotient complet d'ordre 1, les coefficients d'indice 1 à p des deux fractions continues correspondent aux p premiers coefficients de la fraction continue du quotient complet, ils sont donc égaux, de plus les deux fractions continues ont même coefficient d'ordre a0. Les fractions ont donc les mêmes p + 1 premiers coefficients.
-
- La différence entre deux réduites successives est :
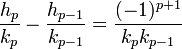
C'est une conséquence de la dernière des propriétés du paragraphe précédent :
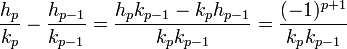
-
- Les réduites de rangs pairs et impairs définissent deux suites adjacentes convergeant vers x :
La formule précédente permet de calculer hp+2/kp+2 - hp/kp.
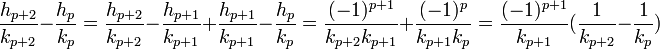
On en déduit que la suite des réduites de rangs pairs est croissante et celle des réduites de rangs impairs décroissante. L'écart entre deux termes consécutifs est inférieur à 2-p. Ceci démontre que les suites sont adjacentes.
-
- La valeur x est la limite de la série alternée :
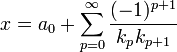
La valeur x est la limite de la suite (hp/kp), qui s'écrit encore :
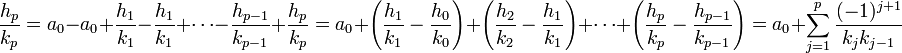
Un passage à la limite sur p montre le résultat voulu.
-
- Pour tout entier p, la différence entre x et la réduite de rang p est donnée par la formule suivante :
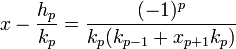
L'expression du réel x en fonction des premiers coefficients de son développement en fraction continue et d'un quotient complet permet d'obtenir :
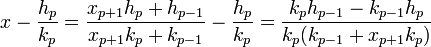
La dernière proposition du paragraphe précédent permet de conclure.
-
- Les majorations suivantes sont vérifiées :
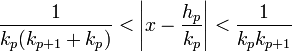
Il suffit de remarquer que xp+1 est plus grand que 1 pour la majoration de gauche. Pour celle de droite, il suffit de remarquer que xp+1 est plus grand que ap+1 et que ap+1.kp - kp-1 est égal à kp+1.

















































