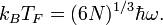Gaz de fermions dégénéré - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Un gaz de fermions dégénéré possède un comportement qui n'est plus décrit par la physique classique mais par la physique quantique. Un gaz entre dans ce régime purement quantique lorsque sa température est suffisamment basse. Par définition, la température en dessous de laquelle la physique classique n'est plus pertinente est appelée la température de Fermi.
En 1995 furent produits les premiers condensats de Bose-Einstein gazeux, ouvrant la voie à l'étude des gaz quantiques. En 1999, l'équipe de Deborah Jin, du laboratoire NIST-JILA (Université du Colorado, USA), refroidit pour la première fois un gaz de fermions dans le régime de dégénérescence quantique.
Refroidissement d'un gaz de fermions
Refroidir un gaz de fermions est plus difficile que pour un gaz de bosons. En effet, en dessous d'une température de l'ordre du mK, i.e. bien avant d'entrer dans le régime dégénéré, les collisions entre fermions identiques dans le même état interne sont fortement inhibées par le principe de Pauli, ce qui limite l'efficacité du refroidissement par évaporation. Deux voies ont été empruntées pour contourner cette limitation : on prépare le gaz dans un mélange d'états internes avant l'évaporation, et les collisions se font entre atomes d'états internes différents, ou bien on refroidit le gaz par thermalisation avec un gaz de bosons simultanément présent (on parle alors de refroidissement sympathique).
On parvient ainsi à produire un gaz de 104 à 106 atomes fermioniques à une température de l'ordre de 0.2TF.
Interactions dans un gaz de fermions dégénéré
Les interactions entre fermions identiques dans le même état interne sont fortement inhibées à basse température. Cependant on peut préparer un mélange ultrafroid de fermions identiques dans deux états de spin différents ; les collisions entre atomes de spins différents sont alors autorisées. La plupart des études faites à ce jour concernent des gaz à deux espèces de spin en proportions égales.
De plus, on peut exploiter le phénomène de résonance de Feshbach pour varier à souhait la force des interactions en plongeant le gaz dans un champ magnétique ajustable. Selon la valeur des interactions, les atomes peuvent s'apparier en molécules qui forment alors un condensat de Bose-Einstein, s'apparier en paires de Cooper pour former un état BCS (Bardeen-Cooper-Schrieffer, voir ci-dessous), et, dans le cas intermédiaire, former un état à N corps complexe qui résiste aux études théoriques et qui pourrait s'avérer intéressant pour l'étude de la supraconductivité à haute température critique.
Effets de la statistique fermionique
Deux fermions identiques ne pouvant être dans le même état, il est clair qu'à suffisamment basse température les prédictions de la physique classique (distribution statistique de Maxwell-Boltzmann) perdent leur sens, puisqu'elles prévoient que les états de plus basse énergie sont occupés par plusieurs particules.
La théorie quantique prévoit qu'à température nulle, si le gaz contient N particules, les N états de plus basse énergie sont chacun occupés par un fermion exactement, et les autres sont vides. L'énergie seuil à partir de laquelle l'occupation des états devient nulle est par définition l'énergie de Fermi ; la température de Fermi TF est simplement l'énergie de Fermi divisée par la constante de Boltzmann.
Pour un gaz de fermions identiques sans interaction, piégé dans un potentiel harmonique de pulsation ω, on a
Les gaz de fermions ultrafroids produits actuellement contiennent typiquement 105 atomes piégés à une fréquence ω de l'ordre de 2π* 100 Hz. La température de Fermi est alors de l'ordre du μK.