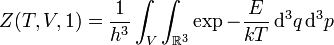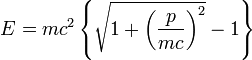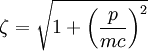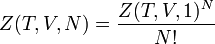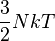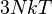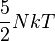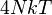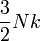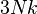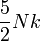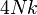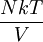Gaz parfait relativiste - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Le gaz parfait relativiste est un modèle de théorie cinétique des gaz qui considère un gaz composé de particules relativistes n'interagissant pas entre elles. Contrairement au gaz parfait « classique » qu'il généralise, il prend en compte les particules animées de vitesses proches de celle de la lumière.
Gaz non quantique
Fonction de partition
La fonction de partition du gaz parfait relativiste monoatomique (particules sans degrés de liberté internes comme la rotation ou vibration des particules) est :
-
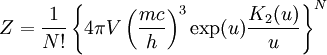
où :
-
-
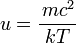
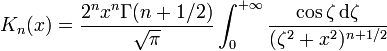
avec
- T la température ;
- N le nombre de particules du gaz ;
- m la masse de chaque particule
- V le volume occupé par le gaz ;
- c la vitesse de la lumière ;
- h la constante de Planck ;
- k la constante de Boltzman.
La fonction de partition dans l'ensemble canonique d'un gaz parfait relativiste à 1 particule est :
où
est l'énergie cinétique de la particule. En séparant les variables, on obtient
-
![Z(T, V, 1) = \frac {4\pi V}{h^3} \exp u \int_0^{+\infty} \exp \left[ -u\sqrt{1 + \left(\frac{p}{mc}\right)^2 }\right] p^2 \,\text{d}p](https://static.techno-science.net/illustration/Definitions/autres/9/9074d3f97973e542fb6965f1631317df_a5a49e8cf3d29bc1ce5f37264dc04f90.png)
![Z(T, V, 1) = \frac {4\pi V}{h^3} \exp u \int_0^{+\infty} \exp \left[ -u\sqrt{1 + \left(\frac{p}{mc}\right)^2 }\right] p^2 \,\text{d}p](https://static.techno-science.net/illustrationWebp/Definitions/autres/9/9074d3f97973e542fb6965f1631317df_a5a49e8cf3d29bc1ce5f37264dc04f90.png)
en posant u = mc2 / kT. Le changement de variable
donne
-
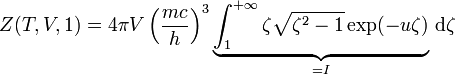
Par parties
- .
Le résultat se trouve en utilisant l'absence d'interaction entre particules :
Variables thermodynamiques
| Variable | Expression générale | Limite classique | Limite ultra-relativiste |
|---|---|---|---|
| énergie interne U |
![Nmc^2 \left[ \frac{K_1(u)}{K_2(u)} + \frac{3}{u} - 1\right]](https://static.techno-science.net/illustrationWebp/Definitions/autres/d/dab4d4bd5687e19afc66963b9213898b_7873e26bf1472ce4fc09e5619aef2037.png)
|
|
|
| énergie libre F |
![-NkT \left\{ \log \left[ \frac{4\pi V}N \left(\frac{mc}h\right)^3 \frac{K_2(u)}{u} \right] + 1 \right\} - Nmc^2](https://static.techno-science.net/illustrationWebp/Definitions/autres/e/e188b79c83ba30e6084177195a3037fa_69fc4d379947bf934a096aab6f8db7cc.png)
| ||
| enthalpie H |
![Nmc^2 \left[ \frac{K_1(u)}{K_2(u)} + \frac{4}{u} - 1\right]](https://static.techno-science.net/illustrationWebp/Definitions/autres/e/e1d14a49d250699fa853fbc66ba96946_e3e6a3d141fad993f1dfe37a40226539.png)
|
|
|
| enthalpie libre G |
![-NkT \log \left[ \frac{4\pi V}N \left(\frac{mc}h\right)^3 \frac{K_2(u)}{u} \right] - Nmc^2](https://static.techno-science.net/illustrationWebp/Definitions/autres/d/d3cf87073b810ac8dc0511a95f6003a6_a446b8529709174c260f1b21b2c1ff85.png)
| ||
| capacité calorifique C |
![N k u \left\{ u + \frac 3{u} - \frac{K_1(u)}{K_2(u)} \left[ 3 + u\frac{K_1(u)}{K_2(u)}\right] \right\}](https://static.techno-science.net/illustrationWebp/Definitions/autres/6/6def1945995c85fe8d0cd3e3584bc5ec_22988135b84eb08feed4c0a431e9bf63.png)
|
|
|
| capacité calorifique C |
![N k u \left\{ u + \frac 4{u} - \frac{K_1(u)}{K_2(u)} \left[ 3 + u\frac{K_1(u)}{K_2(u)}\right] \right\}](https://static.techno-science.net/illustrationWebp/Definitions/autres/a/a87e0491eb4761aa19784736984267ca_c175bc8ef3161c1f6816ca5968bde6bc.png)
|
|
|
| potentiel chimique μ |
![-kT \log \left[ \frac{4\pi V}N \left(\frac{mc}h\right)^3 \frac{K_2(u)}{u} \right] - mc^2](https://static.techno-science.net/illustrationWebp/Definitions/autres/a/afdd68c6fc0bb4d406a5b2b424f0c791_74d2e7714d46ba611939f33ee10c7a32.png)
| ||
| entropie S |
![Nk \left\{ \log \left[ \frac{4\pi V}N \left(\frac{mc}h\right)^3 \frac{K_2(u)}{u} \right] + 4 + \frac{K_1(u)}{K_2(u)}\right\}](https://static.techno-science.net/illustrationWebp/Definitions/autres/b/b0364dda71b3e4824c411b171bccac54_fbf05e77f9e6c864e94dbd0142dc6819.png)
| ||
| pression P |
|
|
|
Bibliographie
Ouvrages généraux
- Walter Greiner, Ludwig Neise, Horst Stöcker, Hubert Curien, H. Aksas, Thermodynamique et mécanique statistique, Springer, 1999
Références
- , p. 269-271
- Les grandes lignes suivent , p. 269-271. L'intégration finale utilise un autre changement de variables.
- (en) Le lien entre l'intégrale et la fonction de Bessel K est donné par Modified Bessel Function of the Second Kind sur MathWorld, Equation 7
- Expressions générales données par , p. 271-273
