Groupe ponctuel de symétrie - Définition

Introduction

En chimie, un groupe ponctuel de symétrie est un sous-groupe d'un groupe orthogonal : il est composé d'isométries, c'est-à-dire d'applications linéaires laissant invariants les distances et les angles. Le groupe ponctuel de symétrie d'une molécule est constitué des isométries qui laissent la molécule, en tant que forme géométrique, invariante.

Cristallographie

Figure 1 : exemple de rotation

Figure 2 : exemple d'inversion

Figure 3 : la combinaison d'une rotation d'ordre 2 et d'inversion est une réflexion

Figure 4 : exemple de réflexion

En cristallographie, un groupe ponctuel contient les opérations de symétrie qui laissent invariants la morphologie d’un cristal et ses propriétés physiques (la symétrie de la structure atomique d’un cristal est décrite par les groupes d’espace). Ils sont classés en groupes holoèdres et mérièdres, selon qu’ils décrivent la symétrie complète du réseau ou qu’ils soient des sous-groupes de ceux-ci. L'existence d'un réseau périodique comporte des restrictions sur l'ordre des rotations, qui en deux et trois dimensions sont limitées aux valeurs 1, 2, 3, 4 et 6, alors que ces restrictions ne s'appliquent pas aux objets non périodiques comme les molécules.

Cette question relève d'un problème mathématique plus général, les termes utilisés étant alors un peu différents. Elle correspond à l'analyse du groupe orthogonal d'un réseau. Un réseau est l'équivalent d'un espace vectoriel, à la différence que les scalaires sont les nombres entiers et non pas des éléments d'un corps. Le groupe orthogonal est le groupe des applications linéaires conservant les distances et les angles.

Opérations de symétrie et chiralité

Les opérations ponctuelles sont de deux types :

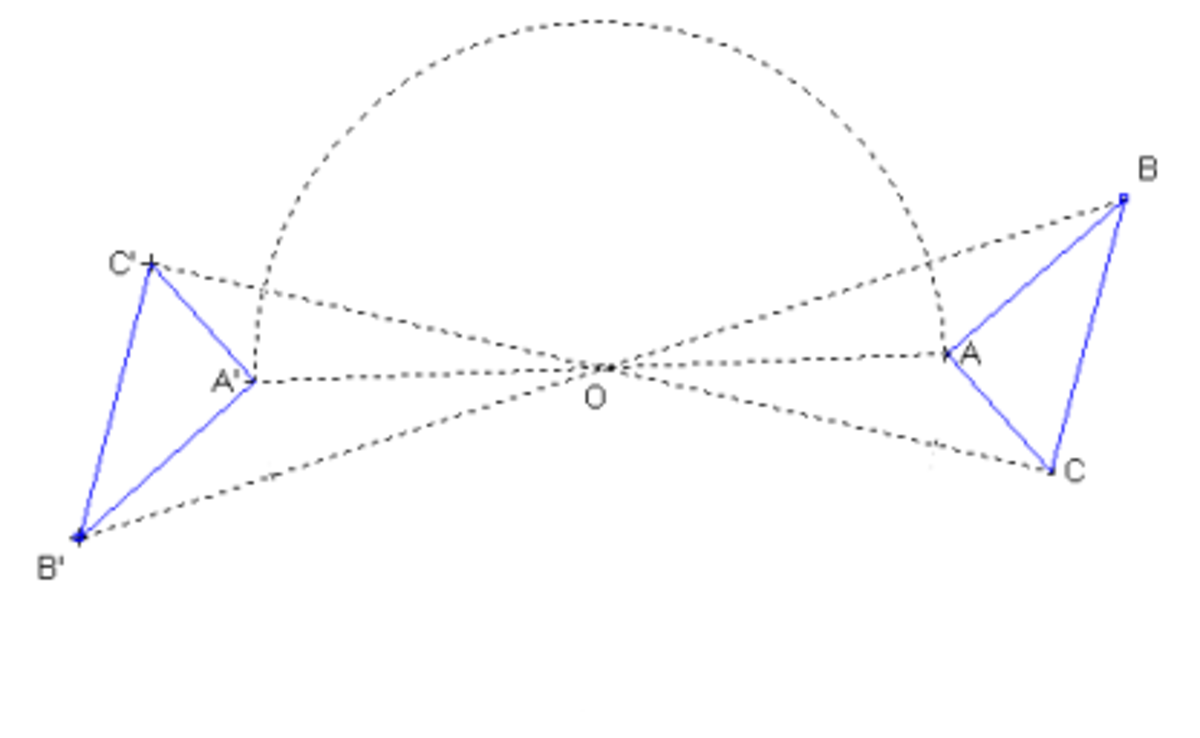
• opérations de première espèce, qui ne changent pas la chiralité de l’objet sur lequel elles agissent ; il s’agit de rotations pures (Figure 1) ;
• opérations de seconde espèce, qui changent la chiralité de l’objet sur lequel elles agissent ; il s’agit de roto-inversions, opérations composées d’une rotation suivie d’une inversion, c'est-à-dire d'une symétrie par rapport à un point, appelé centre d’inversion (voir Figure 2).

À chaque opération de première espèce, on peut associer une opération de seconde espèce qui transforme le barycentre de l’objet comme l’opération de première espèce qui lui est associée. Lorsque l’objet n'est pas chiral, le résultat de l’application de ces deux opérations de symétrie est identique.

Note : dans des espaces à plus de 3 dimensions (non utilisés en cristallographie), de nouvelles espèces apparaissent où la chiralité est conservée dans une partie des dimensions mais inversée dans une autre partie : il s’agit de symétries « partielles » par rapport à un plan ou tout sous-espace possédant au moins 2 dimensions en moins par rapport à l’espace d’origine, ces symétries partielles pouvant se combiner sans nécessairement rétablir la chiralité d’origine mais en donnant des opérations d’autres espèces. Leur ordre de combinaison est alors important, les opérations n’étant pas nécessairement symétriques (ni même nécessairement associatives dans les espaces non euclidiens).

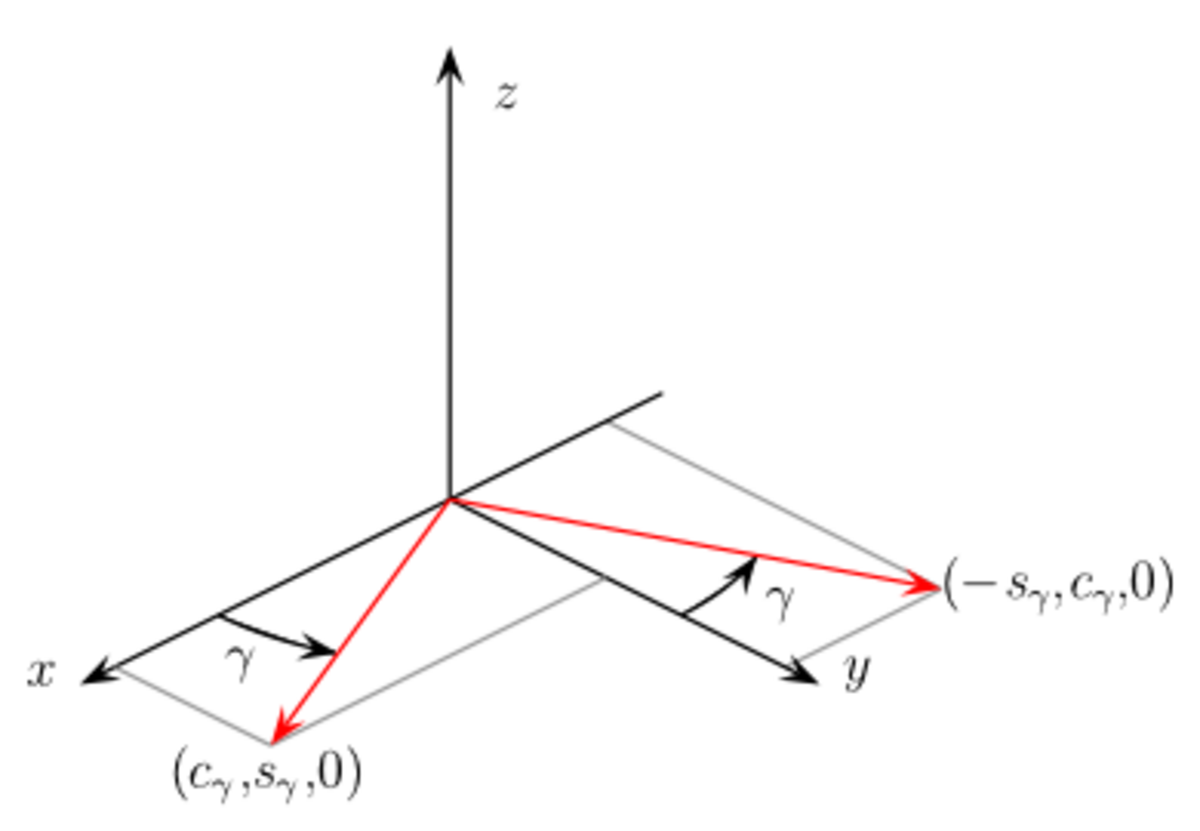
Une rotation d'angle 2π/n est indiquée par n dans la notation de Hermann-Mauguin, ou par C dans la notation de Schoenflies.

• n représente l'ordre de la rotation, c'est-à-dire le nombre de fois où la rotation doit être appliquée pour retrouver la situation d’origine.
• Dans un cristal, à cause de la périodicité de la structure, exprimée par son réseau, les valeurs de n sont limitées à 1, 2, 3, 4 et 6 (dans les espaces à deux et trois dimensions), qui correspondent aux rotations qui permettent un pavage périodique infini de l’espace.

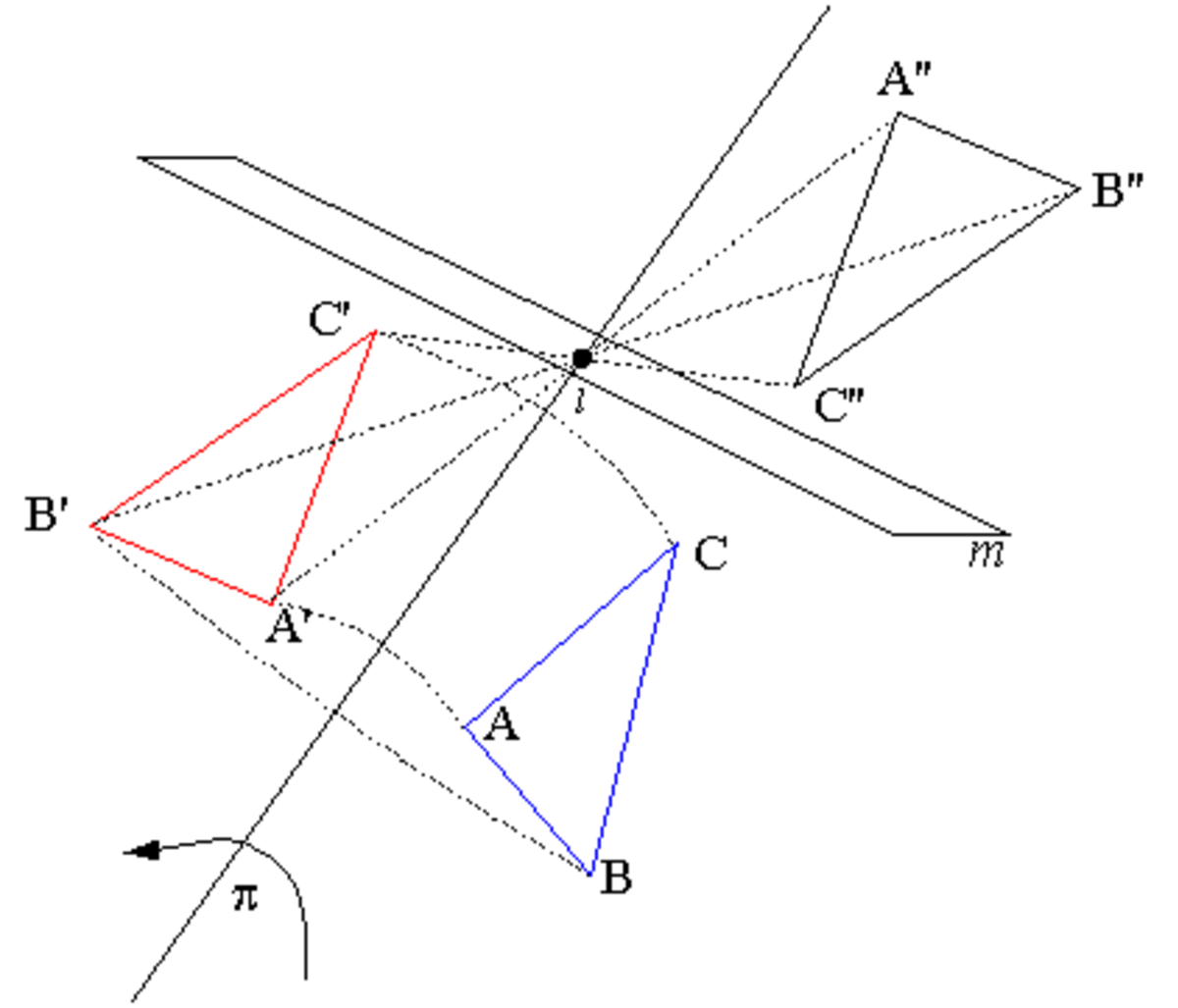
Une roto-inversion composée d'une rotation d'ordre n et d'une inversion est indiquée par n.

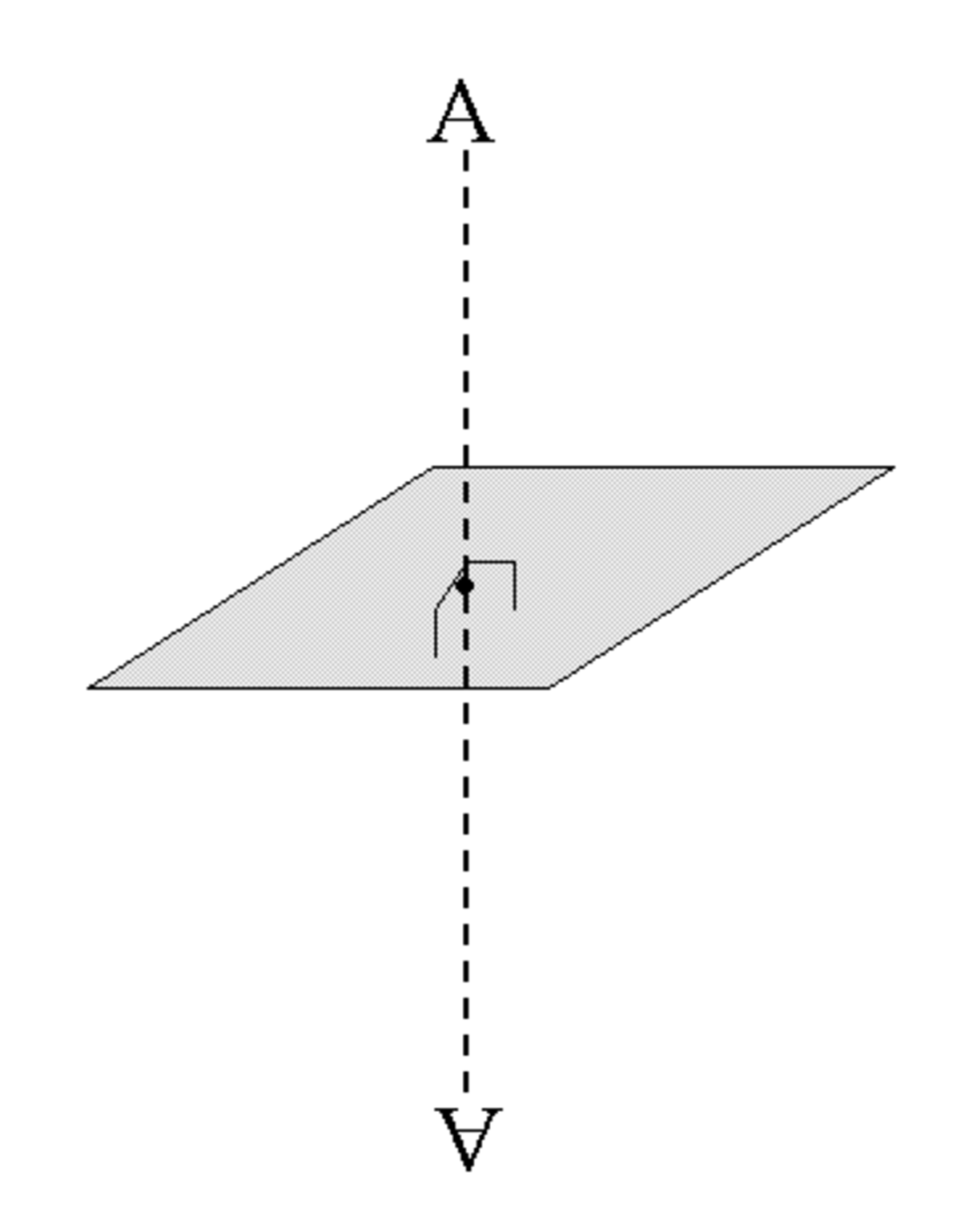
• En chimie, les opérations de seconde espèce sont plus fréquemment nommées roto-réflexions que roto-inversions, car on préfère les décomposer en une rotation suivie d’une réflexion (i.e. d'une symétrie orthogonale par rapport à un plan, voir Figure 4), le plan de la réflexion étant perpendiculaire à l’axe de la rotation. Elles sont alors indiquées par en notation de Hermann-Mauguin, ou par S dans la notation de Schoenflies, où n représente l'ordre de la rotation qui apparaît dans cette seconde décomposition.
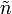
• 1 est l'inversion pure.
• 2 correspond à une rotation de π suivie d’une inversion (Figure 3), ce qui est équivalent à une réflexion par rapport à un plan perpendiculaire à l’axe de la rotation. Cette opération est plus fréquemment indiquée comme m, réflexion par rapport à un miroir.

Les opérations de symétrie ponctuelle sont finalement classées de la manière suivante :

• les rotations pures, qui sont notées par leur ordre, n ;
• les réflexions, qui sont notées par la lettre m (comme miroir) ;
• l'inversion, qui est notée 1 (notation de Hermann-Mauguin), i, ou C_i (notation de Schoenflies) ;
• les roto-inversions, qui sont des opérations composées d’une rotation suivie d’une inversion, sont notées par n, où n est l'ordre de la rotation.