Mathématiques de la relativité générale - Définition
La liste des auteurs de cet article est disponible ici.
L'espace-temps comme une variété
La plupart des approches modernes de la relativité générale se basent sur le concept de variété. Plus précisément, la construction physique de base représentant la gravitation – un espace-temps courbe – est modélisée par une variété pseudo-riemanienne lorentzienne à quatre dimensions, continue, connexe et constituant un espace séparé ou espace de Hausdorff. Les autres grandeurs physiques sont représentées par différents tenseurs (voir plus loin).
L'objectif dans le choix d'une variété comme structure mathématique de base est de pouvoir refléter au mieux les propriétés physiques. Par exemple, dans la théorie des variétés, chaque point p est contenu dans un voisinage muni d'un système de coordonnées appelé carte, et peut être pensé comme une représentation locale de l'espace-temps autour de l'observateur (représenté par le point p). La carte munie de son système de coordonnées permet de décrire localement l'espace autour du point de la variété. Le principe de covariance de Lorentz local, qui affirme que les lois de la relativité restreinte s'appliquent localement en chaque point de l'espace-temps, fournit une raison supplémentaire pour le choix de la variété pour représenter l'espace-temps : on peut préciser ce point en affirmant que localement autour d'un point d'une variété, la région « ressemble » à un espace de Minkowski (espace-temps plat).
L'idée d'une carte munie d'un système de coordonnées comme un observateur local pouvant effectuer des mesures à proximité a aussi un sens du point de vue physique, car cela correspond à la manière de fonctionner pour les mesures expérimentales – effectuées localement. Pour des problèmes cosmologiques, une carte peut être un voisinage relativement grand. En revanche, la description complète de l'espace-temps entier nécessite en général plusieurs cartes, regroupées au sein d'un atlas.
Structure globale et structure locale
Une distinction importante en physique consiste à considérer la différence entre les structures locale et globale. Les mesures en physique sont effectués dans une région de l'espace-temps relativement petite. On comprend alors pourquoi étudier la structure locale de l'espace-temps en relativité générale, alors que déterminer la topologie de l'espace-temps a du sens, spécialement en cosmologie afin de déterminer la structure globale de l'espace-temps.
Dérivées de tenseurs
Avant l'arrivée de la relativité générale, les modifications dans les processus physiques étaient généralement décrites par des dérivées partielles, permettant par exemple de modéliser les champs électromagnétiques (voir Équations de Maxwell). Même en relativité restreinte, les dérivées partielles sont suffisantes pour décrire de telles modifications. Cependant, en relativité générale, il est apparu que les dérivées s'appliquant aux tenseurs doivent être utilisées.
Le problème pour définir les dérivées sur des variétés qui ne sont pas « plates » est qu'il n'existe pas de manière naturelle pour comparer des vecteurs en des points différents. Une structure supplémentaire sur les variétés est nécessaire pour définir les dérivées. Les paragraphes suivants décrivent deux dérivées importantes qui peuvent être définies en imposant une structure supplémentaire sur les variétés dans les deux cas.
Connexions affines
La courbure sur une variété connectée peut être caractérisées intrinsèquement en prenant un vecteur en un point et en le transportant parallèlement le long d'une courbe de la variété. Bien que comparer des vecteurs en différents points n'est généralement pas un processus bien défini, une connexion affine

La connexion affine est une application linéaire faisant correspondre à deux champs de vecteurs (
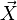
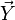
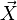
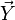
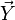
Une connexion affine importante est la connexion de Levi-Civita, qui est une connexion symétrique qui résulte du transport parallèle d'un vecteur tangent le long d'une courbe tout en conservant le produit scalaire de ce vecteur le long de la courbe. Les coefficients de connexion résultant sont appelés symboles de Christoffel et peuvent être calculés directement à partir de la métrique. Pour cette raison, ce type de connexion est souvent appelé une connexion métrique.
Dérivée covariante
Le champ de vecteurs
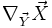
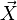
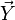
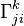
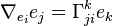
Malgré la première apparence, les coefficients de connexion ne sont pas les composants d'un tenseur.
Dans un système de coordonnées, la dérivée covariante de X le long de Y est alors
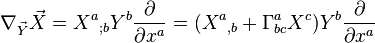
L'expression entre parenthèses, appelée la dérivée covariante de X relativement à la connexion et notée
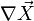
La dérivée covariante de X peut ainsi être vue comme un opérateur différentiel agissant sur un champ de vecteurs et lui faisant correspondre un champ de tenseurs de type (1,1) (augmentant l'index de covariance de 1). Elle peut être généralisée pour agir sur des champs de tenseurs de type (r,s) et lui faisant correspondre un champ de tenseurs de type (r,s + 1). La notion de transport parallèle peut alors être définie de la même manière que dans le cas des champs vectoriels.
La dérivée de Lie
La dérivée de Lie est une autre dérivée de tenseur importante. Tandis que la dérivée covariante nécessite une connexion affine pour permettre la comparaison entre des vecteurs en différents points, la dérivée de Lie utilise la congruence d'un champ de vecteurs pour répondre au même besoin. L'idée de faire glisser une fonction le long d'une congruence amène à la définition de la dérivée de Lie, où une fonction « glissée » est comparée à la valeur de la fonction originale en un point donné. La dérivée de Lie peut être définie pour des champs de tenseurs de type (r,s) et peut être vue comme une carte qui associe un tenseur type (r,s) à un autre tenseur de type (r,s).
La dérivée de Lie est généralement notée