Vendredi 2 Mai 2025
Rechercher 🔍

Mathématiques de la relativité générale - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
- Introduction - Pourquoi les tenseurs ? - Tenseurs en relativité générale - L'espace-temps comme une variété - Dérivées de tenseurs - Champs de tenseurs en relativité générale - Le tenseur énergie-impulsion - Le tenseur de courbure de Riemann - Les équations de géodésique - Aspects mathématiques

Les équations de géodésique

Une fois l'équation d'Einstein résolue pour obtenir la métrique, il reste à déterminer le mouvement des objets inertiels dans l'espace-temps. En relativité générale, on suppose que le mouvement inertiel a lieu le long de géodésiques de l'espace-temps, paramétrisées à l'aide de la variable temps propre. Les géodésiques sont des courbes qui transportent parallèlement leur propre vecteur tangent \vec U . 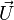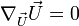On écrit alors cette condition par \nabla_ {\vec U} \vec U =0 , qui constitue l'équation géodésique. 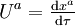Il est possible de décrire cette dernière en fonction d'un système de coordonnées xa en prenant le vecteur tangent U^a= \tfrac{\mathrm dx^a}{\mathrm d \tau}  :

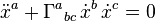
\ddot{x}^a + {\Gamma^a}_{bc} \, \dot{x}^b \, \dot{x}^c = 0

où le point désigne la dérivée d / dτ par rapport au temps propre τ choisi comme paramétrisation de la courbe dans le cas où la courbe est de genre temps. Dans le cas d'une courbe de genre lumière, on ne peut choisir le temps propre comme coordonnée et il est alors nécessaire d'utiliser un paramètre affine. On observe alors la présence des symboles de Christoffel dans l'équation.

Une caractéristique principale de la relativité générale est de permettre de déterminer le chemin parcouru par des particules test ainsi que la trajectoire des rayons lumineux dans un champ gravitationnel. Il suffit pour cela de résoudre les équations géodésiques.

Les équations d'Einstein relient la distribution totale de matière-énergie à la courbure de l'espace-temps. Leur grande non-linéarité rend difficile la détermination exacte du mouvement précis de la matière dans un espace-temps courbe. Par exemple, dans un système composé d'une planète en orbite autour d'une étoile, le mouvement de la planète est déterminé en résolvant les équations du champ gravitationnel qui font intervenir le tenseur énergie-impulsion de la planète et de l'étoile. Le champ gravitationnel de la planète affecte la géométrie entière de l'espace-temps et par conséquent le mouvement des objets. Il est par conséquent raisonnable que les équations du champ gravitationnel déterminent les équations géodésiques.

Aspects mathématiques

Nécessité d'une théorie relativiste de la gravitation

Mathématiquement, la force de gravitation de Newton dérive d'une énergie potentielle. Le potentiel de gravitation associé à cette énergie potentielle obéit à l'équation de Poisson, qui n'est pas covariante sous transformation de Lorentz. La théorie de la gravitation de Newton n'est donc pas compatible avec le principe fondamental de relativité restreinte énoncé par Einstein en 1905.

Ce principe étant supposé avoir une validité universelle, Einstein va chercher une théorie de la gravitation qui soit compatible avec lui. Le résultat de sa quête est la théorie de la relativité générale.

Modélisation de l'espace-temps

Notre perception intuitive nous indique que l'espace-temps apparait régulier et continu, c'est-à-dire « sans trous ». Mathématiquement, ces propriétés vont se traduire par le fait que l'espace-temps sera modélisé par une variété différentielle lisse à 4 dimensions M4, c'est-à-dire un espace à 4 dimensions pour lequel le voisinage de chaque point ressemble localement à un espace euclidien à 4 dimensions.

Géométrie de l'espace-temps

Cet article suit les conventions de signe classiques de MTW

Il adopte également la convention de sommation d'Einstein.

Tenseur métrique

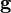
La variété différentielle M est munie d'une métrique lorentzienne définie par un tenseur métrique \mathbf g , et constitue ainsi une variété lorentzienne, qui constitue un cas particulier de variété pseudo-riemannienne (le qualificatif « lorentzienne » sera précisé plus loin dans le texte ; cf. ).

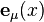
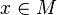
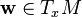
Soit un système de coordonnées quelconque xμ autour d'un point P, et soient {\mathbf e}_{\mu}(x) une base locale de TxM, espace tangent à la variété au point x \in M . Un vecteur tangent \mathbf w \in T_xM s'écrit alors comme la combinaison linéaire :

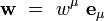
\mathbf{w} \ = \ w^{\mu} \ \mathbf{e}_{\mu}

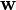
Les wμ sont appelée les composantes contravariantes du vecteur \mathbf w . Le tenseur métrique \mathbf g est la forme bilinéaire symétrique :

\mathbf g \ = \ g_{\mu \nu}(x) \ \mathrm dx^{\mu} \ \otimes \mathrm d x^{\nu}

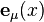
où dxμ désigne la base duale de {\mathbf e}_{\mu}(x) dans l'espace cotangent T_x^*M , c'est-à-dire la forme linéaire sur TxM telle que :

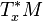
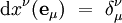
\mathrm dx^{\nu}({\mathbf e}_{\mu})\ = \ \delta_{\mu}^\nu

Les composantes gμν(x) du tenseur métrique varient de manière continue dans l'espace-temps.

Le tenseur métrique peut ainsi être représenté par une matrice 4×4 réelle symétrique :

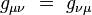
g_{\mu \nu} \ = \ g_{\nu \mu}

Or, toute matrice 4×4 réelle possède a priori 4 × 4 = 16 éléments indépendants. La condition de symétrie réduit ce nombre à 10 : il reste en effet les 4 éléments diagonaux, auxquels il faut ajouter (16 − 4)/2 = 6 éléments non diagonaux. Le tenseur gμν possède donc seulement 10 composantes indépendantes.

Produit scalaire

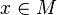
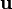
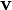
Le tenseur métrique définit pour chaque point x \in M de la variété un pseudo-produit scalaire (pseudo au sens où l'hypothèse de positivité est retirée ; cf. métrique lorentzienne) dans l'espace TxM euclidien tangent à M au point x. Si \mathbf u et \mathbf v sont deux vecteurs de TxM, leur produit scalaire s'écrit :

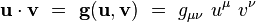
\mathbf u \cdot \mathbf v \ = \ \mathbf g (\mathbf u, \mathbf v) \ = \ g_{\mu \nu} \ u^{\mu} \ v^{\nu}

En particulier, en prenant deux vecteurs de base, on obtient les composantes :

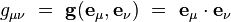
g_{\mu \nu} \ = \ \mathbf g ({\mathbf e}_{\mu}, {\mathbf e}_{\nu}) \ = \ {\mathbf e}_{\mu} \cdot {\mathbf e}_{\nu}

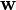
Remarque : wμ désignant les composantes contravariantes du vecteur \mathbf w , on peut définir de même ses composantes covariantes par :

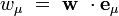
w_{\mu} \ = \ \mathbf w \ \cdot \mathbf e_{\mu}

Distance élémentaire

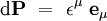
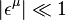
Considérons le vecteur déplacement élémentaire \mathrm d\mathbf P \ = \ \epsilon^{\mu} \ \mathbf e_{\mu} entre le point P et un point infiniment voisin : | \epsilon^{\mu} | \ll 1 . Sa norme infinitésimale invariante est le nombre réel noté ds2, et on a  :

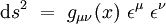
\mathrm ds^2 \ = \ g_{\mu \nu}(x) \ \epsilon^{\mu} \ \epsilon^{\nu}

Si l'on note « à la physicienne » εμ = dxμ les composantes du vecteur déplacement élémentaire, la longueur infinitésimale s'écrit formellement :

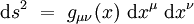
\mathrm ds^2 \ = \ g_{\mu \nu}(x) \ \mathrm dx^{\mu} \ \mathrm dx^{\nu}

Attention : dans cette formule, dxμ représente un nombre réel qui s'interprète physiquement comme la « variation infinitésimale » de la coordonnée xμ, et non une forme différentielle !

Métrique lorentzienne

Précisons maintenant l'expression lorentzienne, qui signifie que le tenseur métrique est de signature (1,3). Le principe d'équivalence assure qu'on peut effacer localement un champ de gravitation en prenant un système de coordonnées localement inertiel bien choisi. Dans un tel système de coordonnées localement inertiel Xα autour du point P précédent, l'invariant ds2 s'écrit :

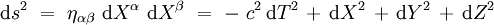
\mathrm ds^2 \ = \ \eta_{\alpha \beta} \ \mathrm dX^{\alpha} \ \mathrm dX^{\beta} \ = \ - \ c^2 \,\mathrm dT^2 \, + \, \mathrm dX^2 \, + \, \mathrm dY^2 \, + \, \mathrm dZ^2

où ηαβ est la métrique plate de Minkowski. On adopte ici la convention de signe MTW :

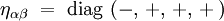
\eta_{\alpha \beta} \ = \ \mathrm{diag} \ ( -, \, +, \, +, \, + \, )

On utilisera ici les conventions usuelles suivantes :

  • un indice grec varie de 0 à 3. Il est associé à une grandeur dans l'espace-temps.
  • un indice latin varie de 1 à 3. Il est associé aux composantes spatiales d'une grandeur dans l'espace-temps.

Par exemple, le 4-vecteur position s'écrit dans un système de coordonnées localement inertiel :

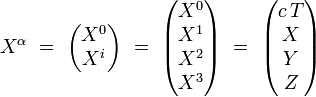
X^{\alpha} \ = \ \left( \begin{matrix} X^{0} \\ X^{i} \end{matrix} \right) \ = \ \left( \begin{matrix} X^{0} \\ X^{1} \\ X^{2} \\ X^{3} \end{matrix} \right) \ = \ \left( \begin{matrix} c \, T \\ X \\ Y \\ Z \end{matrix} \right)

Le caractère lorentzien de la variété M assure ainsi que l'espace euclidien tangent à M possède en chaque point un pseudo-produit scalaire (pseudo au sens où l'hypothèse de positivité est retirée) ayant 3 valeurs propres strictement positives (associées à l'espace) et une valeur propre strictement négative (associée au temps). En particulier, l'intervalle élémentaire de temps propre séparant deux évènements vérifie :

\mathrm d \tau^2 \ = \ - \ \frac{\mathrm ds^2}{c^2} \ > \ 0

Notions générales de connexion & dérivée covariante

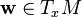
D'une manière générale, on appelle connexion \nabla un opérateur qui associe à un champ de vecteurs \mathbf V du fibré tangent TM un champ d'endomorphismes \nabla \mathbf V de ce fibré. Si {\mathbf w} \in T_xM est un vecteur tangent au point x \in M , on note usuellement :

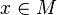
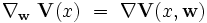
\nabla_{\mathbf w} \ \mathbf V(x) \ = \ \nabla \mathbf V(x,\mathbf w)

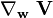
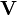
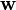
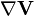
On dit que \nabla_{\mathbf w} \ \mathbf V est la dérivée covariante du vecteur \mathbf V dans la direction {\mathbf w} . On impose de plus à \nabla \mathbf V de vérifier la condition supplémentaire que, pour toute fonction f, on ait :

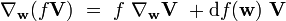
\nabla_{\mathbf w} (f \mathbf V) \ = \ f \ \nabla_{\mathbf w} \mathbf V \ + \mathrm df(\mathbf w) \ \mathbf V

La dérivée covariante vérifie les deux propriétés de linéarité suivantes :

  • linéarité en w, c'est-à-dire que, quels que soient les champs de vecteurs w et u et les nombres réels a et b, on ait :
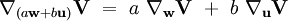
    \nabla_{(a \mathbf w + b \mathbf u)} \mathbf V \ = \ a \ \nabla_{\mathbf w} \mathbf V \ + \ b \ \nabla_{\mathbf u} \mathbf V
  • linéarité en V, c'est-à-dire que, quels que soient les champs de vecteurs X et Y et les nombres réels a et b, on ait :
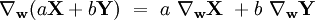
    \nabla_{\mathbf w} (a\mathbf X + b\mathbf Y) \ = \ a \ \nabla_{\mathbf w} \mathbf X \ + b \ \nabla_{\mathbf w} \mathbf Y

Une fois que la dérivée covariante est définie pour les champs de vecteurs, elle peut être étendue aux champs tensoriels en utilisant la règle de Leibniz : si \mathbf T et \mathbf S sont deux tenseurs quelconques, on impose que :

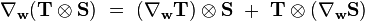
\nabla_{\mathbf w}(\mathbf T \otimes \mathbf S) \ = \ (\nabla_{\mathbf w} \mathbf T )\otimes \mathbf S \ + \ \mathbf T \otimes(\nabla_{\mathbf w} \mathbf S)

La dérivée covariante d'un champ de tenseurs le long d'un vecteur \mathbf w est à nouveau un champ de tenseurs du même type.

Connexion associée à la métrique

On définit la connexion de Levi-Civita [1] comme étant l'unique connexion vérifiant en plus des conditions précédentes que, pour tous champs de vecteurs X, Y, Z de TM, on ait :

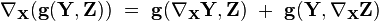
  • \nabla_{\mathbf X}(\mathbf g(\mathbf Y,\mathbf Z)) \ = \ \mathbf g(\nabla_{\mathbf X} \mathbf Y,\mathbf Z) \ + \ \mathbf g(\mathbf Y,\nabla_{\mathbf X} \mathbf Z) (parallélisme).
  • \nabla_{\mathbf X} \mathbf Y \ - \ \nabla_{\mathbf Y} \mathbf X \ = \ [\mathbf X, \mathbf Y] , où [\mathbf X,\mathbf Y] est le crochet de Lie de X et Y (torsion nulle).

Description en coordonnées

La dérivée covariante d'un vecteur est un vecteur, et peut ainsi être exprimée comme une combinaison linéaire de tous les vecteurs de base :

\nabla_{\mathbf w} V \ = \ \left[ \, \nabla_{\mathbf w} V \, \right]^\rho \ \mathbf e_\rho \ = \ \Gamma^\rho \ \mathbf e_\rho

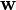
où Γρ représente la composante du vecteur dérivée covariante dans la direction \mathbf e_\rho (cette composante dépend du vecteur \mathbf w choisi).

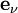
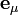
Pour décrire la dérivée covariante il suffit de décrire celle de chacun des vecteurs de base \mathbf e_\nu le long de la direction \mathbf e_\mu . On définit alors les symboles de Christoffel Γρμν dépendants de 3 indices par :

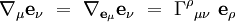
\nabla_{\mu} {\mathbf e}_{\nu} \ = \ \nabla_{{\mathbf e}_{\mu}} {\mathbf e}_{\nu} \ = \ \Gamma^\rho {}_{\mu \nu} \ {\mathbf e}_\rho

La connexion de Levi-Civita est entièrement caractérisée par ces symboles de Christoffel. Appliquons en effet la formule générale :

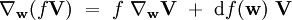
\nabla_{\mathbf w} (f \mathbf V) \ = \ f \ \nabla_{\mathbf w} \mathbf V \ + \ \mathrm df(\mathbf w) \ \mathbf V

sous la forme :

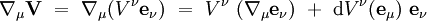
\nabla_{\mu} \mathbf V \ = \ \nabla_{\mu} (V^\nu \mathbf e_\nu) \ = \ V^\nu \ (\nabla_{\mu} \mathbf e_\nu ) \ + \ \mathrm dV^\nu(\mathbf e_\mu) \ \mathbf e_\nu

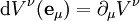
Sachant que \mathrm dV^\nu(\mathbf e_\mu) = \partial_\mu V^\nu , on obtient :

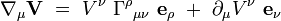
\nabla_{\mu} \mathbf V \ = \ V^\nu \ \Gamma^\rho {}_{\mu \nu} \ {\mathbf e}_\rho \ + \ \partial_\mu V^\nu \ \mathbf e_\nu

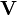
Le premier terme de cette formule décrit la « déformation » du système de coordonnées par rapport à la dérivée covariante, et le second les changements de coordonnées du vecteur \mathbf V . Les indices sommés étant muets, on peut réécrire cette formule sous la forme :

\nabla_{\mu} \mathbf V \ = \ \left[ \, V^\rho \ \Gamma^\nu {}_{\mu \rho} \ + \ \partial_\mu V^\nu \, \right] \ \mathbf e_\nu

On en déduit la formule importante pour les composantes :

\nabla_{\mu} \mathbf{V}^{\nu} \ = \ \left[ \, \nabla_{\mu} \mathbf{V} \, \right]^{\nu} \ = \ \partial_{\mu} V^{\nu} \ + \ \Gamma_{~ \mu \rho}^{\nu} \ V^{\rho}

En utilisant la formule de Leibniz, on démontrerait de même que :

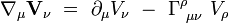
\nabla_{\mu} \mathbf{V}_{\nu} \ = \ \partial_{\mu} V_{\nu} \ - \ \Gamma_{~ \mu \nu}^{\rho} \ V_{\rho}

Pour calculer explicitement ces composantes, les expressions des symboles de Christoffel doivent être déterminées à partir de la métrique. On les obtient aisément en écrivant les conditions suivantes :

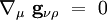
\nabla_{\mu} \ \mathbf{g}_{\nu \rho} \ = \ 0

Le calcul explicite de cette dérivée covariante conduit à :

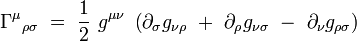
\Gamma^\mu {}_{\rho \sigma} \ = \ \frac{1}{2} \ g^{\mu \nu} \ \left(\partial_\sigma g_{\nu \rho } \ + \ \partial_\rho g_{\nu \sigma} \ - \ \partial_\nu g_{\rho \sigma} \right)

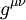
où g^{\mu \nu}\ sont les composantes du tenseur métrique inverse, définies par les équations :

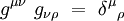
g^{\mu \nu} \ g_{\nu \rho} \ = \ \delta^\mu{}_\rho

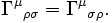
Les symboles de Christoffel ont une symétrie par rapport aux indices du bas : \Gamma^\mu {}_{\rho \sigma}=\Gamma^\mu {}_{\sigma \rho}.\

Remarque : on définit parfois aussi les symboles suivants :

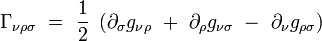
\Gamma_{\nu \rho \sigma} \ = \ \frac{1}{2} \ \left(\partial_\sigma g_{\nu \rho } \ + \ \partial_\rho g_{\nu \sigma} \ - \ \partial_\nu g_{\rho \sigma} \right)

tels que :

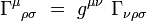
\Gamma^\mu {}_{\rho \sigma} \ = \ g^{\mu \nu} \ \Gamma_{\nu \rho \sigma}

Tenseur de courbure de Riemann

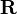
Le tenseur de courbure de Riemann \mathbf R est le tenseur d'ordre 4 défini pour tous champs de vecteurs X, Y, Z de M par :

\mathbf R(\mathbf X,\mathbf Y)\mathbf Z \ = \ \nabla_{\mathbf X} \, (\nabla_{\mathbf Y} \mathbf Z) \ - \ \nabla_{\mathbf Y} \, (\nabla_{\mathbf X} \mathbf Z) \ - \ \nabla_{[\mathbf X,\mathbf Y]} \mathbf Z

Ses composantes s'écrivent explicitement en termes de la métrique :

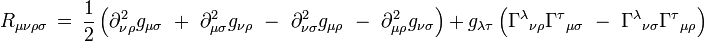
R_{ \mu \nu \rho \sigma } \ = \ \frac{1}{2}\left( \partial^2_{ \nu \rho } g_{ \mu \sigma } \ + \ \partial^2_{ \mu \sigma } g_{ \nu \rho } \ - \ \partial^2_{ \nu \sigma } g_{ \mu \rho } \ - \ \partial^2_{ \mu \rho } g_{ \nu \sigma } \right) \ + \ g_{ \lambda \tau } \left( \Gamma^\lambda {}_{ \nu \rho } \Gamma^\tau {}_{ \mu \sigma } \ - \ \Gamma^\lambda {}_{ \nu \sigma } \Gamma^\tau {}_{ \mu \rho } \right)

Les symétries de ce tenseur sont :

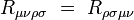
R_{ \mu \nu \rho \sigma } \ = \ R_{ \rho \sigma \mu \nu }\
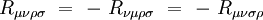
R_{ \mu \nu \rho \sigma } \ = \ - \ R_{ \nu \mu \rho \sigma } \ = \ - \ R_{\mu \nu \sigma \rho }

Il vérifie de plus la relation :

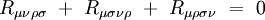
R_{ \mu \nu \rho \sigma } \ + \ R_{ \mu \sigma \nu \rho } \ + \ R_{ \mu \rho \sigma \nu } \ = \ 0

Tenseur de courbure de Ricci

Le tenseur de Ricci est le tenseur d'ordre 2 défini par contraction du tenseur de courbure de Riemann :

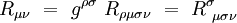
R_{\mu \nu} \ = \ g^{\rho \sigma} \ R_{\rho \mu \sigma \nu} \ = \ R^\sigma_{~ \mu \sigma \nu}

Ses composantes s'écrivent explicitement en fonction de la métrique :

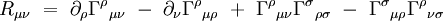
R_{\mu \nu} \ = \ \partial_{\rho} \Gamma^{\rho} {}_{\mu \nu} \ - \ \partial_{\nu} \Gamma^{\rho} {}_{\mu \rho} \ + \ \Gamma^{\rho} {}_{\mu \nu} \Gamma^{\sigma} {}_{\rho \sigma} \ - \ \Gamma^{\sigma} {}_{\mu \rho}\Gamma^{\rho} {}_{\nu \sigma}

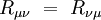
Ce tenseur est symétrique : R_{\mu \nu} \ = \ R_{\nu \mu}\ .

Courbure scalaire

La courbure scalaire est l'invariant défini par contraction du tenseur de Ricci avec la métrique :

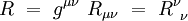
R \ = \ g^{\mu \nu} \ R_{\mu \nu} \ = \ R^\nu_{~ \nu}

Équation d'Einstein

L’équation complète du champ gravitationnel, qu'on appelle l'équation d'Einstein, s’écrit :

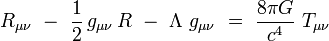
R_{\mu \nu} \ - \ \frac{1}{2} \, g_{\mu \nu} \, R \ - \ \Lambda \ g_{\mu \nu} \ = \ \frac{8 \pi G}{c^4} \ T_{\mu \nu}

où Λ est la constante cosmologique, c est la vitesse de la lumière dans le vide, G est la constante gravitationnelle qui apparaît aussi dans la loi de la gravitation newtonienne, et Tμν le tenseur énergie-impulsion.

Le tenseur symétrique gμν possédant 10 composantes indépendantes, l'équation tensorielle d'Einstein est équivalente à un système de 10 équations scalaires indépendantes. Ce système aux dérivées partielles non linéaires couplées est le plus souvent très difficile à étudier.

Tenseur énergie-impulsion

Le tenseur énergie-impulsion peut s'écrire sous la forme d'une matrice 4×4 réelle symétrique :

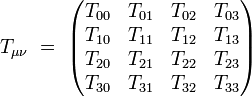
T_{\mu \nu} \ = \ \left( \begin{matrix} T_{00} & T_{01} & T_{02} & T_{03} \\ T_{10} & T_{11} & T_{12} & T_{13} \\ T_{20} & T_{21} & T_{22} & T_{23} \\ T_{30} & T_{31} & T_{32} & T_{33} \end{matrix} \right)

On y retrouve les grandeurs physiques suivantes :

  • T00 est la densité volumique d'énergie. Elle est positive.
  • T10, T20, T30 sont les densités de moments.
  • T01, T02, T03 sont les flux d'énergie.
  • La sous-matrice 3×3 des composantes spatiale-spatiale :
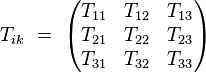
T_{ik} \ = \ \left( \begin{matrix} T_{11} & T_{12} & T_{13} \\ T_{21} & T_{22} & T_{23} \\ T_{31} & T_{32} & T_{33} \end{matrix} \right)

est la matrice des flux de moments. En mécanique des fluides, sa diagonale correspond à la pression, et les autres composantes correspondent aux efforts tangentiels dus à la viscosité.

Pour un fluide au repos, le tenseur énergie-impulsion se réduit à la matrice diagonale diag(ρc2,p,p,p) où ρ est la masse volumique et p la pression hydrostatique.

Le tenseur de courbure de Riemann
- Introduction - Pourquoi les tenseurs ? - Tenseurs en relativité générale - L'espace-temps comme une variété - Dérivées de tenseurs - Champs de tenseurs en relativité générale - Le tenseur énergie-impulsion - Le tenseur de courbure de Riemann - Les équations de géodésique - Aspects mathématiques
miniature
La face cachée de la Lune révèle une étrangeté 🌓
miniature
Piéger le CO2 sous terre indéfiniment, c'est possible ! 🌍
miniature
La plus lointaine cousine de la Voie Lactée jamais observée 🌀
miniature
Ce codex médiéval cache un secret dans son bois 🔍
miniature
Une éruption volcanique en 2018 responsable d'une explosion de vie 🌋
miniature
Un système d'exploitation pour les ordinateurs quantiques voit le jour 🖥️
miniature
Des singularités temporelles dans l'Univers ? 🕰️
miniature
Des fossiles de dinosaures mieux datés 🦖
miniature
Une gigantesque muraille de 10 milliards d'années-lumière dans l'Univers 🔭
miniature
Benchmark: les processeurs quantiques sous la loupe, quels sont les meilleurs ? 🏆
miniature
Découverte d'une "fourmi de l'enfer" vieille de 113 millions d'années 🐜
miniature
Le rôle méconnu de la décharge dans l'usure des batteries 🔋
miniature
1
La fonte des glaces déplace les pôles: quelles conséquences ? 🌍
miniature
L'appareil photo de votre smartphone peut détecter l'antimatière 📱
miniature
Cette étoile-zombie peut déformer les atomes à distance, et elle fonce dans notre galaxie ⭐
miniature
Un mosasaure géant découvert dans le Mississippi 🦕
miniature
Problème, les galaxies meurent plus tôt que prévu 🌀
miniature
Ce lien entre cannabis et troubles psychotiques 🧠
miniature
Une révolution dans le refroidissement des puces électroniques ? 🔥
miniature
Des parasites sous-marins filmés en train de vampiriser un poisson des abysses 👀
miniature
Lucy survole un astéroïde en forme de cacahuète 🚀
miniature
Découverte du fossile d'un dinosaure géant méconnu 🦕
miniature
Mars avait-elle un champ magnétique unilatéral ? 🔍
miniature
Des chimpanzés surpris à sociabiliser avec de l'alcool 🍇
miniature
Découverte macabre: ce gladiateur a été tué par un lion il y a 1 800 ans... en Grande-Bretagne 🦁
miniature
L'électroluminescence du graphène, une découverte inattendue ! 💡
miniature
Cet objet métallique n'a pas été fabriqué sur Terre 🔧
miniature
1
Cette innovation permet aux voitures électriques de charger 6 fois plus vite par grand froid ⚡
miniature
Cette super-Terre brûle les attentes des astronomes 🔥
miniature
Découverte exceptionnelle de fossiles d'amphibiens géants 🐸
miniature
Voici ce qui a causé les toutes premières inégalités de richesse 💰
miniature
Quelle est cette zone étrange dans l'Atlantique Nord ? 🌊
miniature
Cette planète orbite à angle droit autour de deux étoiles, une première ! 🔭
miniature
Des cellules solaires flexibles battent des records d'efficacité ⚡
miniature
Ce dispositif reproduit les trous noirs et trous blancs en laboratoire 🌀
miniature
Record établi pour un transistor en diamant 💎
miniature
Les sursauts radio rapides trahissent enfin leur origine cosmique 📡
miniature
Ces biomarqueurs sanguins prédisent la démence 10 ans à l'avance 🧠
miniature
Découverte majeure: des médicaments 23 fois plus efficaces contre le cancer 💊
miniature
Les oscillations collectives des foules humaines denses 🔁
miniature
Une forme inconnue de la matière détectée au LHC ? ⚛️
miniature
Le sel, un facteur méconnu de l'obésité ? 🧂
miniature
L'Univers en rotation, une réponse élégante à ce problème astrophysique majeur 🌀
miniature
Découverte tectonique majeure sous les Petites Antilles 🌍
miniature
1
Peut-on geler en chauffant ? ❄️
miniature
Une peau électronique pour doter les robots du sens du toucher 👌
miniature
Invention d'un bois semi-transparent avec une technique...surprenante ! 🌳
miniature
Le cancer inscrit dans nos gènes dès la naissance ? 🧬
miniature
Des supernovae à l'origine de deux extinctions massives sur Terre ? 💥
miniature
Le passé verdoyant du plus grand désert du monde 🐪
Page générée en 0.204 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise