Mathématiques de la relativité générale - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Les mathématiques de la relativité générale se réfèrent à différentes structures et techniques mathématiques utilisées par la théorie de la relativité générale d'Albert Einstein. Les principaux outils utilisés dans cette théorie géométrique de la gravitation sont les champs tensoriels définis sur une variété pseudo-riemannienne représentant l'espace-temps.
Pourquoi les tenseurs ?
Le principe de relativité généralisé (ou principe de covariance généralisée, ou encore covariance sous la transformation) affirme que les lois de la Physique prennent les mêmes formes mathématiques dans tous les référentiels et a été l'un des principes centraux dans le développement de la relativité générale. Le terme de « covariance généralisée » a été utilisé lors de la formulation initiale de la relativité générale, mais est maintenant connu sous le nom de covariance par difféomorphisme. Bien que la covariance par difféomorphisme ne soit pas l'élément central de la relativité générale et qu'une controverse soit toujours présente concernant son statut dans la théorie, la propriété d'invariance des lois de la Physique associée au fait que la relativité générale soit une théorie essentiellement géométrique (dans le cadre de la géométrie non-riemannienne) suggèrent que soient utilisés les tenseurs dans sa formulation. Ceci sera discuté plus bas.
Tenseurs en relativité générale
La description de phénomènes physiques ne doit pas dépendre de qui fait les mesures – un système de coordonnées n'est pas meilleur qu'un autre. L'une des conséquences profondes de la théorie de la relativité a été la suppression de référentiels préférentiels. Le relativité restreinte a mis fin aux référentiels inertiels pour la description des phénomènes physiques, alors de la relativité générale a éliminé tout référentiel privilégié pour une telle description.
Tout observateur peut faire des mesures et les quantités numériques obtenues dépendent seulement du système de coordonnées utilisé. Ceci suggère une manière de formuler la relativité en utilisation des structures invariantes qui sont indépendantes du système de coordonnées (représenté par l'observateur) utilisé, et qui aient une existence propre. L'outil mathématique le plus adapté pour cela semblait être le tenseur. Pour exemple, lors de la mesure des champs électriques et magnétiques produits par les charges accéléerées, les valeurs des champs dépendront du système de coordonnées utilisé, mais les champs sont considérés comme ayant une existence indépendante, représentée par le tenseur de champ électromagnétique, répondant à la formulation tensorielle des équations de Maxwell.
Mathématiquement, les tenseurs sont des opérateurs linéaires généralisés. Ils sont souvent considérés comme une représentation de fonctions multilinéaires. Ainsi les idées de l'algèbre linéaire sont utilisées pour étudier les tenseurs.
A chaque point p d'une variété V peuvent être construits les espaces tangent TpV et cotangent
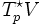
Ces deux espaces vectoriels peuvent être utilisés pour construire des tenseurs de type (r,s) en p. Ces tenseurs sont des graphes multilinéaires de valeur réel agissant sur la somme directe de r copies de l'espace cotangent à M en p d'une part avec s copies de l'espace tangent à M en p d'autre part. L'ensemble de tous ces graphes multilinéaires forment un espace vectoriel, appelé l'espace produit tensoriel de type (r,s) en p et noté par (Tp)rsM. Si l'espace tangent est de dimension n, il peut être démontré que
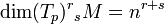
Dans la littérature sur la relativité générale, il est conventionnel d'utiliser la convention des composants pour les tenseurs. Un tenseur de type (r,sr) peut être écrit :

où
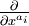
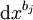
Du fait que l'espace-temps est supposé de dimension 4, chaque index d'un tenseur ne peut prendre qu'un des 4 valeurs possibles. De ce fait, le nombre total d'éléments d'un tenseur vaut 4R, où R est la somme du nombre des indices covariants et contravariants du tenseur (ce nombre est appelé rang du tenseur).
Tenseurs symétriques et antisymétriques
Certaines quantités physiques peuvent être représentés par des tenseurs dont tous les composants ne sont pas indépendants. On peut notamment citer les exemples des tenseurs symétriques et antisymétriques. Les tenseurs antisymétriques sont couramment utilisés pour représenter des rotations (par exemple, le tenseur de vorticité).
Bien qu'un tenseur générique de rang R et de dimension 4 ait 4R composants, des contraintes sur ce tenseur telles que la symétrie ou l'antisymétrie permettent de réduire le nombre de composants distincts. Par exemple, un tenseur de rang 2 T symétrique vérifie Tab = Tba et possède 10 composants indépendants, alors qu'un tenseur de rang 2 P antisymétrique vérifie Pab = − Pba et possède 6 composants indépendants. Pour des rangs supérieurs à 2, les paires d'indexs symétriques et antisymétriques doivent être explicitement identifiés.
Les tenseurs antisymétriques de rang 2 jouent des rôles importants en théorie de la relativité. L'ensemble de tous ces tenseurs – souvent appelés bivecteurs – forment un espace vectoriel de dimension 6, parfois appelé espace bivectoriel.
Le tenseur métrique
Le tenseur métrique est un objet central en relativité générale. Il décrit la géométrie locale de l'espace-temps (en temps de résultat de la résolution de l'équation d'Einstein). En utilisation l'approximation des champs faibles, la métrique peut aussi être considérée comme la représentation d'un potentiel gravitationnel.

















































