Points et parties remarquables de la frontière d'un convexe - Définition
La liste des auteurs de cet article est disponible ici.
Une classe particulière de points extrémaux : les points exposés
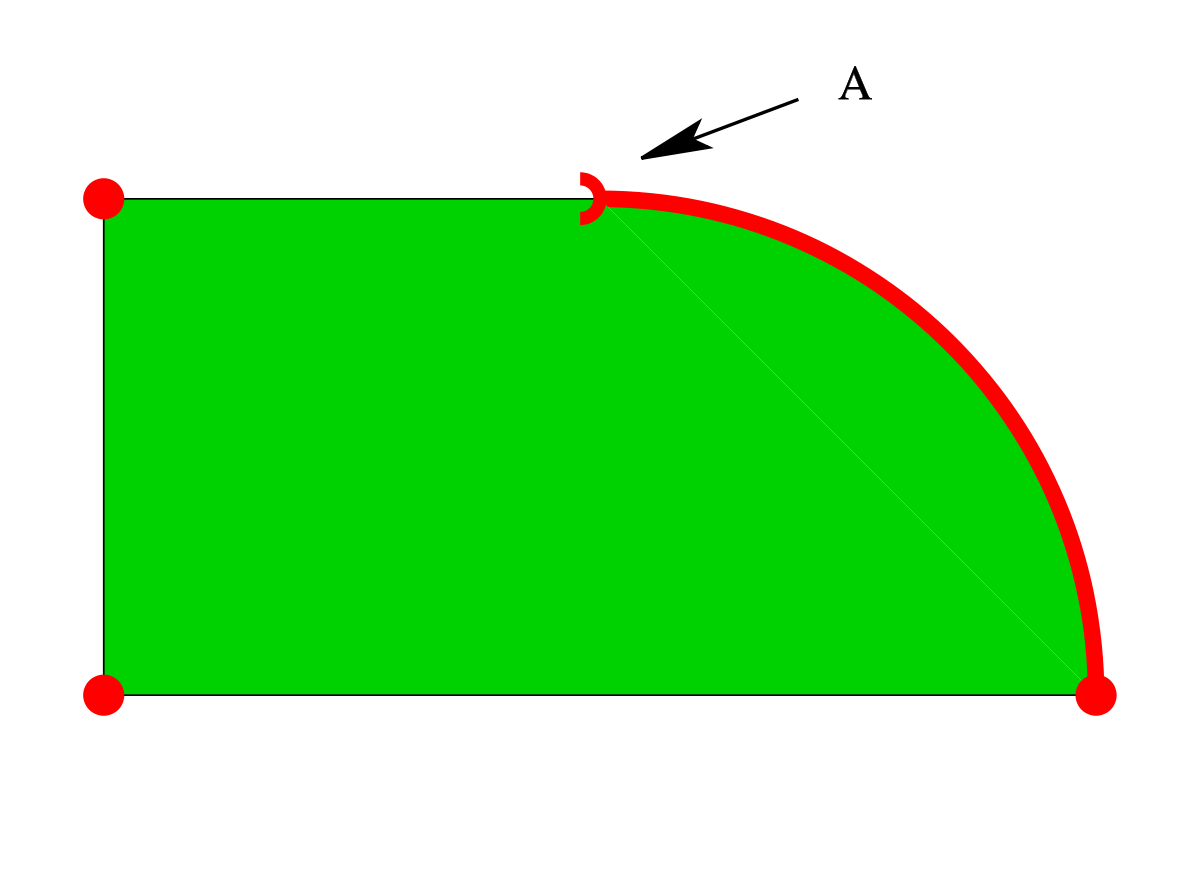
Soit C un convexe et c un point de C. On dit que c est un point exposé de C lorsqu'il existe un hyperplan d'appui H de C vérifiant :
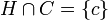
L'énoncé suivant est quasi-évident, mais sa réciproque est fausse, dès la dimension 2 :
Proposition — Tout point exposé est extrémal.
En effet si c est exposé de C, on peut écrire
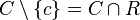
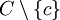
On dispose toutefois, à défaut de réciproque, de l'information suivante (c'est un théorème dû à S. Straszewicz et remontant à 1935) :
Théorème — Dans un convexe fermé en dimension finie, tout point extrémal est limite de points exposés.
Le cas des polyèdres convexes
Les trois notions dont cet article a fait une présentation parallèle coïncident dans le cas particulier important des polyèdres convexes (qu'on définira comme dans l'article Polytope comme étant les intersections d'un nombre fini de demi-espaces dans un espace affine de dimension finie).
Pour ce cas particulier :
Proposition — Dans un polyèdre convexe,
- toute face de la frontière est exposée ;
- l'ordre de chaque point de la frontière est égal à la dimension de l'unique intérieur relatif de face auquel il appartient.
En particulier il y a identité de l'ensemble des sommets et de celui des points extrémaux. Pour un polyèdre convexe compact, le théorème de Minkowski peut donc aussi être énoncé comme assurant qu'il est enveloppe convexe de l'ensemble de ses sommets.
Quelques autres informations relatives à la division en faces d'un polyèdre convexe, qu'on démontre concurremment à la proposition précédente, méritent d'être signalées dans ce rapide survol. Rappelons qu'on appelle facettes d'un convexe de dimension d ses faces de dimension d − 1 :
Proposition — Dans un polyèdre convexe C,
- les facettes sont en nombre fini et couvrent toute la frontière relative, ce sont elles-mêmes des polyèdres convexes ;
- toute face propre de C est elle-même face d'une facette de C.
Une conséquence est qu'on obtient toutes les faces propres en considérant les facettes, puis les facettes des facettes, etc... Les faces sont donc en nombre fini, et en particulier les sommets : tout polyèdre convexe compact est donc l'enveloppe convexe d'un nombre fini de points.
Contextualisations
On prendra garde de ce que le mot « face » n'a pas ici la signification qu'il a dans l'étude des polyèdres traditionnels dans l'espace de dimension 3, celui des éléments plans les bordant. Ici les « faces » vont pouvoir avoir toutes les dimensions, y compris 0 ou 1. Tant les sommets, les arêtes que les « faces » habituelles d'un cube ou d'un tétraèdre seront des faces au sens des définitions qui suivent.
Contextualisation des points exposés : les faces exposées
On va ici commencer par l'extension du concept de « sommets exposés » bien que ce ne soit pas la plus utile, mais parce qu'elle est la plus facile à définir et visualiser : on appelle face exposée d'un convexe C tout ensemble de la forme
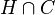
La remarque suivante est alors tautologique :
Remarque — Un point c d'un convexe C est exposé si et seulement si {c} est une face exposée de C.
Les faces exposées de C couvrent toute sa frontière puisqu'il passe un hyperplan d'appui au moins en chaque point de celle-ci.
Contextualisation des points extrémaux : les faces
De même que les points exposés sont les faces exposées de dimension zéro, les points extrémaux sont les faces de dimension zéro où « faces » est défini comme suit :
Une partie F d'un convexe C est dite une face de C lorsque F est un convexe non vide ayant la propriété suivante : si un segment ouvert ]x,y[ tracé dans C rencontre F, alors tout le segment fermé [x,y] est inclus dans F.
Les deux énoncés qui suivent sont de vérification quasi-immédiate, le second se vérifiant de la même façon qu'on a vérifié que les points exposés étaient extrémaux :
Proposition — Un point c d'un convexe C est extrémal si et seulement si {c} est une face de C.
Proposition — Les faces exposées sont des faces.
Vu ce deuxième énoncé, les faces de C (autres que C tout entier qui est l'unique face de dimension maximale) couvrent donc toute la frontière de C.
La réciproque n'en est pas vraie (puisqu'il existe des points extrémaux qui ne sont pas exposés, ils donnent aussitôt un exemple de faces qui ne sont pas des faces exposées), avec toutefois une exception pour les faces de codimension 1, qu'on appelle parfois des facettes :
Proposition — Soit C convexe de dimension finie d. Toute face de C de dimension d − 1 est exposée.
Contrairement aux faces exposées, les faces s'organisent d'une manière hiérarchique particulièrement agréable, comme l'expriment les deux énoncés qui suivent :
Proposition — Si F est une face de C et F1 une face de F, alors F1 est une face de C.
Proposition — Si C est un convexe de dimension finie, les intérieurs relatifs des faces de C forment une partition de celui-ci.
Pour la première proposition, soit c extrémal. Considérons un segment ]x,y[ dans C contenant c. Comme
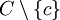
Pour la deuxième proposition, soit F une face exposée et H un hyperplan d'appui avec
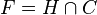
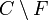
Pour le troisième énoncé, soit F une face de dimension d − 1, H l'hyperplan affine enveloppe affine de F et c un point de l'intérieur relatif de F (c'est-à-dire de son intérieur dans H). Notons
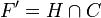
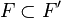
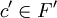
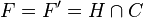
Passons à la quatrième proposition. Soit ]x,y[ un segment ouvert dans C rencontrant F1. A fortiori ce segment rencontre F, qui est une face de C, donc ses extrémités sont dans F. Puisque les faces sont convexes par définition, tout le segment [x,y] est dans F. On a alors un segment dans F dont un point de l'intérieur rencontre F1 ; puisque F1 est une face de F ses deux extrémités sont dans F1.
Reste l'énoncé relatif à la partition par les intérieurs relatifs des faces. On va le montrer par récurrence sur la dimension du convexe, l'initialisation étant évidente (cas d'un point). Supposons donc le vrai pour les convexes de dimension strictement inférieure à k et soit C un convexe de dimension k.
- *La non-vacuité des intérieurs relatifs des faces provient de la condition de non-vacuité exigée des faces elles-mêmes.
- *Pour ce qui est de la réunion des intérieurs relatifs, soit c un point de C. Si c est dans l'intérieur relatif de C, en remarquant que C est lui-même une face, on a exhibé une face dont l'intérieur relatif contient c. Si c est sur la frontière, soit F une face exposée contenant c. Par l'hypothèse de récurrence, c appartient à l'intérieur relatif d'une des faces de F, qui est elle-même par l'énoncé précédent une face de C.
- *Vérifions enfin que deux intérieurs relatifs de faces sont soit égaux soit disjoints. Soit donc F1 et F2 deux faces de C dont les intérieurs relatifs se rencontrent ; notons c un point de leur intersection et G1 et G2 leurs enveloppes affines respectives. On va dans un premier temps montrer que G1 = G2 ; puisque ces sous-espaces affines passent tous deux par c, il suffit pour ce faire de s'assurer qu'ils ont même direction. Soit u un vecteur dans la direction de G1 ; comme c est dans l'intérieur relatif de F1, à condition de prendre α assez petit, les deux points c + αu et c − αu sont tous deux dans F1 donc dans C, tandis que le segment ouvert qui les joint passe par c qui est dans F2. Comme F2 est une face, les extrémités de ce segment sont aussi dans F2 et u appartient bien à la direction de G2. En échangeant les rôles de G1 et G2 on prouve l'égalité. Une fois cette étape passée, en reprenant le même argument qu'à la troisième proposition, on vérifie que
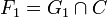
Contextualisation des sommets : le classement des points de la frontière selon leur ordre
En dimension finie, on vient de voir qu'à chaque point de la frontière pouvait être associée une sorte de « dimension », celle de l'unique intérieur relatif de face à laquelle il appartient.
Il y a une deuxième façon de procéder pour associer à chaque point de la frontière d'un convexe de dimension d un entier compris entre 0 et d − 1, apparentée à la définition des « sommets ».
Pour C convexe de dimension finie et c point de la frontière de C. On appelle ordre de c la dimension de l'intersection des hyperplans d'appui à C en c.
Ainsi les sommets sont les points d'ordre nul.
L'exemple très simple d'un disque du plan montre bien que cette notion ne recoupe pas la précédente : sur le cercle qui le borde, tous les points sont extrémaux, donc chaque singleton est à lui seul une face : par la division en faces, on associerait à chaque point l'entier 0. En revanche, il y a une droite d'appui unique en chaque point, et l'ordre est donc partout égal à 1.