Points et parties remarquables de la frontière d'un convexe - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Face à un polyèdre convexe de l'espace de dimension 3, qu'il soit familier comme un cube ou plus exotique, on sait spontanément reconnaître des points où le convexe est « pointu », ses sommets, puis subdiviser les points restants entre points des faces et points des arêtes.
On va ici présenter quelques jeux de définitions qui étendent ces concepts à des ensembles convexes plus généraux, dans n'importe quelle dimension et aux bords possiblement incurvés. Une de ces généralisations, le concept de sommets, est très apparentée à l'intuition qu'on peut avoir de cette notion sur un cube (les points d'une sphère ne seront pas des sommets de la boule qu'elle limite). Les points extrémaux peuvent pour leur être part plus nombreux, suffisamment en fait pour permettre de reconstituer à partir d'eux tout le convexe, et ce même si sa forme est lisse (ainsi dans l'exemple d'une sphère tous les points seront extrémaux).
Après avoir énuméré trois possibles généralisations des sommets d'un cube, l'article fournit deux variantes de la hiérarchie sommets-arêtes-faces, qui ont le bon goût de coïncider dans le cas important des polyèdres convexes.
Les points extrémaux
Définition
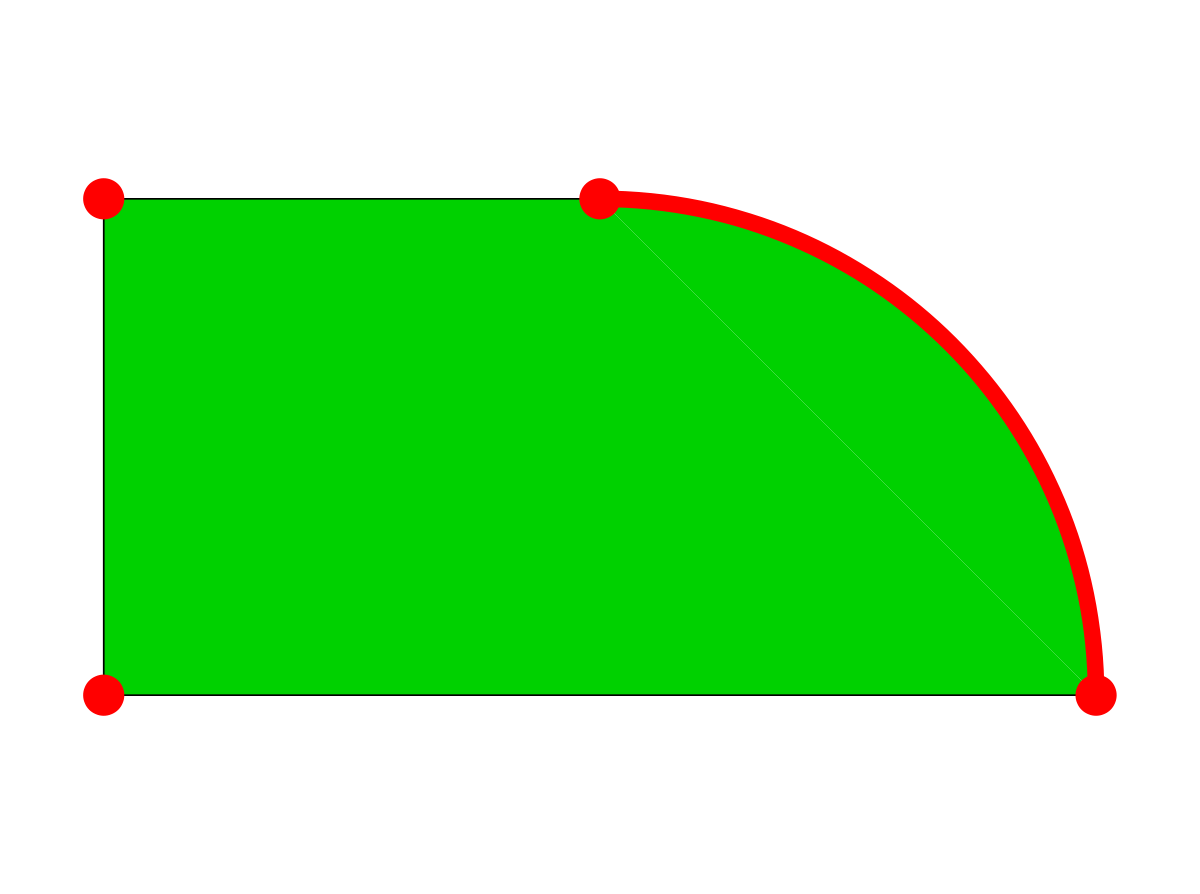
Soit C un convexe et c un point de C. On dit que c est un point extrémal de C lorsque
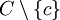
L'ensemble des points extrémaux d'un convexe fermé peut ne pas être fermé, même si l'intuition peut être trompeuse à cause du résultat suivant, qui devient faux à partir de la dimension 3 :
Proposition — Si C est un convexe fermé de dimension 2, l'ensemble de ses points extrémaux est fermé.
Les théorèmes de Minkowski et Krein-Milman
Ce théorème, dû à Hermann Minkowski, permet de reconstituer tout le convexe à partir de ses seuls points extrémaux :
Théorème — Tout convexe compact d'un espace affine de dimension finie est enveloppe convexe de l'ensemble de ses points extrémaux.
La démonstration n'est pas très longue, l'outil essentiel étant le théorème d'existence d'un hyperplan d'appui en tout point de la frontière d'un convexe.
Il peut être généralisé à certains espaces de dimension infinie, à condition d'appliquer in fine l'opérateur de fermeture à l'enveloppe convexe. Ce type d'extension à l'analyse fonctionnelle remonte à 1940, et est l'œuvre des mathématiciens Mark Krein et David Milman.
Théorème — Tout convexe compact d'un espace localement convexe séparé est enveloppe convexe l'adhérence de l'ensemble de ses points extrémaux.
Une classe particulière de points exposés : les sommets
Dans cette section, on travaille exclusivement en dimension finie.
Définition et comparaison avec les points exposés
Soit C un convexe et c un point de C. On dit que c est un sommet de C lorsque c est sur la frontière de C et l'intersection des hyperplans d'appui à C au point c est réduite à {c}.
Proposition — Dans un convexe (en dimension finie), tout sommet est un point exposé.
Notons C le convexe, c le sommet considéré, E l'espace affine ambiant et d sa dimension. On munit E d'une structure euclidienne.
Notons Sc la partie de E formée des vecteurs s vérifiant la condition suivante :
 .
.
Lorsque s n'est pas nul cette condition s'interprète géométriquement : elle signifie que l'hyperplan passant par c et perpendiculaire à s est d'appui en c, le vecteur s pointant du côté opposé à celui du convexe. L'intersection des hyperplans d'appui c'est donc l'ensemble des c + u où u est perpendiculaire à tous les éléments de Sc ; en plus concis c'est
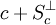
Dire que c est un sommet, c'est dire que cette intersection est réduite à {c}, ce qui revient à dire que
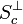
Notons
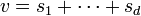
ce qui prouve déjà que l'hyperplan H passant par x et perpendiculaire à v est d'appui en c ; de plus, si x est un point de
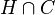
 sont elles-mêmes des égalités (
sont elles-mêmes des égalités (
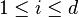
L'ensemble des sommets est au plus dénombrable
Proposition — Un convexe (en dimension finie) possède un ensemble de sommets au plus dénombrable.
On reprend les notations introduites à la démonstration précédente.
Remarquons d'abord que pour tous réels strictement positifs α1,...,αd, le vecteur α1s1 + ... + αdsd est dans Sc et que l'ensemble de ces vecteurs est évidemment un ouvert, ce dont on déduit que Sc est d'intérieur non vide. C'est donc aussi le cas de son translaté c + Sc.
Considérons maintenant un vecteur y de c + Sc ; posons y = c + s, avec s dans Sc. Pour x dans C, examinons le produit scalaire  (où l'inégalité finale provient de la définition même de Sc).
(où l'inégalité finale provient de la définition même de Sc).
Vu la caractérisation variationnelle de la projection sur un convexe fermé, on en conclut que c est la projection
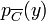
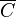
Prenons alors une partie dénombrable dense A de E. Pour tout sommet c du convexe, A rencontre c + Sc (puisque celui-ci est d'intérieur non vide) tandis que