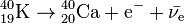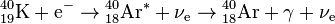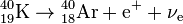Potassium 40 - Définition

Introduction

Le potassium 40, noté ⁴⁰K, est l'isotope du potassium dont le nombre de masse est égal à 40 : son noyau atomique compte 19 protons et 21 neutrons. C'est un radioisotope du milieu naturel, avec un spin 4- pour une masse atomique de 39,96399848 g/mol et une abondance naturelle de 0,0117 % par mole de potassium. Il est caractérisé par un défaut de masse de 33 535 016 ± 271 eV/c² et une énergie de liaison nucléaire de 341 523 214 ± 276 eV.

Radioactivité

Un gramme de potassium 40 présente une radioactivité de 263 kBq.

Sa période radioactive est de 1,248 milliards d'années, pendant laquelle on observe :

• une désintégration β ^– dans 88,8 % des cas pour donner du calcium 40, avec une énergie de désintégration de 1,311 MeV :

• une capture électronique dans 11,2 % des cas pour donner de l'argon 40, avec une énergie de désintégration de 1,505 MeV :

• une désintégration β ⁺, en proportion négligeable en comparaison des deux réactions précédentes (de l'ordre de 0,001 %) :

La seconde réaction (capture électronique) est utilisée pour dater la formation de certaines roches contenant du potassium (méthode de « datation au potassium-argon »), en supposant nulle la quantité initiale d'argon 40 dans ces roches et que l'argon 40 y reste piégé une fois formé.
On notera que le noyau de , nouvellement formé après la capture, se trouve dans un état excité (la capture vers le niveau fondamental est possible, mais rarissime). Il émet un photon lors de la désexcitation.

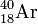
Il est remarquable que le potassium 40 puisse se désintégrer aussi bien en argon 40 qu'en calcium 40, car cela souligne à quel point les noyaux atomiques sont plus stables avec des nombres pairs de protons et de neutrons qu'avec des nombres impairs. De surcroît, la prépondérance de la désintégration en calcium 40 souligne l'effet stabilisateur des « nombres magiques », car, avec 20 neutrons pour 20 protons, le calcium 40 est légèrement déficitaire en neutrons (par rapport aux noyaux stables voisins), mais est stabilisé par le fait qu'il est « doublement magique ».

Dans la mesure où le potassium est un élément indispensable à la vie, le ⁴⁰K constitue la principale source de radioactivité des organismes sains, supérieure à celle constituée par le carbone 14 : un homme de 70 kg subirait chaque seconde la désintégration de 4 400 atomes de ⁴⁰K, soit environ 0,39 mSv/an par le ⁴⁰K contre 0,01 mSv/an imputable au ¹⁴C.

40K et corps humain

Connaissant (a) la quantité totale de potassium dans un corps humain, (b) l'abondance naturelle de ⁴⁰K présent dans la biosphère et (c) la période radioactive de celui-ci, il est facile de calculer le nombre de désintégrations par seconde (Becquerel) qui y ont lieu.

(a) : Quantité totale de potassium dans un corps humain. Celle-ci est en moyenne de 4216 ± 473 mmol (165 ± 18 g) pour un homme et de 4172 ± 540 mmol (163 ± 31 g) pour une femme, mais vu que d'autres paramètres tels que l'âge ou l'IMC peuvent affecter ces valeurs, une formule qui tient compte de ces facteurs a été développée comme suit :

• Pour un homme :

  KCT = (98,3 - 0,1594 × âge + 0,1431 × poids - 0,1848 × taille) × MNG

• Pour une femme :

  KCT = (94,39 - 0,1735 × âge + 0,1169 × poids - 0,1567 × taille) × MNG

Où KCT est le potassium corporel total (en mmol), l'âge est en années, le poids en kg, la taille en cm et MNG est la masse non-grasse (par exemple, pour un corps de 80 kg constitué à 20 % de graisse, la MNG vaut 0,8 x 80 = 64 kg).

(b) : L'abondance naturelle du ⁴⁰K est de 0,01167 % (cf. table des isotopes du potassium).

(c) : La période radioactive du ⁴⁰K (1,277×10⁹ ans) permet de calculer pour une quantité donnée de l'isotope (une mmol, soit 6,022 x 10²⁰ atomes), le nombre de désintégrations par unité de temps (en Bq). En l'occurrence, une mmol de ⁴⁰K produira :

(6,022 × 10²⁰ × ln2 / (1,277×10⁹ × 365,25 × 24 × 60 × 60)= 1,036 × 10⁴ Bq

Finalement, il suffit de calculer KCT × 0,0001167 × 1,036 ×10⁴ pour obtenir le nombre de Bq produits par le ⁴⁰K dans un corps humain, ce qui en moyenne (valeurs minimales et maximales des KCT indiqués plus haut) donne donc entre 4390 et 5670 désintégrations par seconde (Bq). Ces valeurs sont à comparer à celles données en exemple dans la page Becquerel, où les valeurs indiquées pour l'être humain tiennent compte de façon similaire des autres isotopes naturellement présents dans le corps.

À noter qu'il est inutile de vouloir mesurer cette radioactivité à l'aide d'un compteur Geiger : les rayonnements bêta moins du ⁴⁰K ne traversent que très peu la matière telle que celle qui constitue les liquides corporels ou la peau et sont donc absorbés par les atomes des molécules environnantes, qui peuvent alors subir des ionisations. Cette mesure doit donc se faire par d'autres méthodes telles que l'homogénéisation de l'échantillon biologique suivie de la détection de son activité bêta moins par comptage de scintillation. Dans les cellules, l'ionisation de certains atomes due à la radioactivité du ⁴⁰K peut provoquer la rupture de liaisons chimiques et aboutir à la formation de radicaux libres, qui sont généralement détoxifiés par une variété d'enzymes spécialisées. Si l'ionisation intervient sur des atomes qui constituent l'ADN des chromosomes, ceci peut parfois provoquer des mutations aux conséquences plus ou moins graves pour la cellule ou pour l'individu.