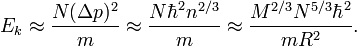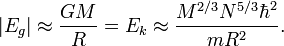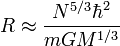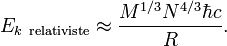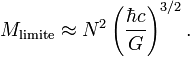Relation masse-rayon des naines blanches - Définition

Introduction

Au derniers stades de son évolution, lorsqu'une étoile ayant une masse comprise entre 0,17 et 1,33 masse solaire s'effondre sur elle-même, il en résulte une naine blanche. Cet astre, aussi lumineux qu'une étoile classique à une taille plus petite de plusieurs ordres de grandeur. La matière dont elle est faite est dite dégénérée car elle est si compressée qu'une cuillère à café pèse plusieurs tonnes. Plus sa masse augmente, plus la matière « dégénère », les électrons se rapprochant du noyau atomique sous l'effet de la pression. Ainsi plus l'astre est massif, plus il est petit. La relation masse-rayon des naines blanches fût établie en 1930 par le physicien indien Subrahmanyan Chandrasekhar alors âgé de 20 ans lors d'un voyage en paquebot vers Bombay.

Relation approximée

Il existe une relation approchée entre la masse et le rayon d'une étoile de type naine blanche, en utilisant l'argument de la minimisation de l'énergie. Son énergie peut être approchée en prenant la somme de son énergie gravitationnelle et de son énergie cinétique interne (essentiellement celle des électrons). Le potentiel d'énergie gravitationnelle d'un morceau de masse unitaire de naine blanche, E, sera de l'ordre de :

E = − GM/R,

où G représente la constante gravitationnelle, M la masse de la naine blanche, et R son rayon.

L'énergie cinétique de la masse unitaire E_k, provient en premier lieu du mouvement des électrons, aussi sera-t-elle approximativement :

N p²/m,

où p représente le moment moyen de l'électron, m sa masse, et N le nombre d'électrons par unité de masse.
Puisque les électrons sont dégénérés, nous pouvons estimer que p est de l'ordre de l'incertitude sur le moment, Δp, donnée par le principe d'incertitude, qui pose que Δp ∙ Δx est de l'ordre de la constante de Planck réduite ħ. Δx sera de l'ordre de la distance moyenne entre les électrons, qui sera approximativement n^−1/3, c'est-à-dire l'inverse de la racine cubique de la densité, n, d'électrons par unité de volume. Puisque il y a N M électrons dans la naine blanche et que son volume est de l'ordre de R³, n sera de l'ordre de N M / R³. Pour calculer l'énergie cinétique par unité de masse, E_k, nous trouvons que :

La naine blanche sera à l'équilibre lorsque la totalité de son énergie, E_g + E_k, sera minimale. À ce point, les énergies cinétique et gravitationnelle ont des valeurs absolues comparables, aussi nous pouvons déduire une relation approchée entre la masse et le rayon en écrivant :

La solution pour le rayon, R, donne :

En abandonnant N qui ne dépend que de la composition de la naine blanche, et les constantes universelles, nous restons alors avec une relation entre la masse et le rayon :

,

Relation rayon-masse pour une naine blanche modèle.

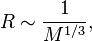
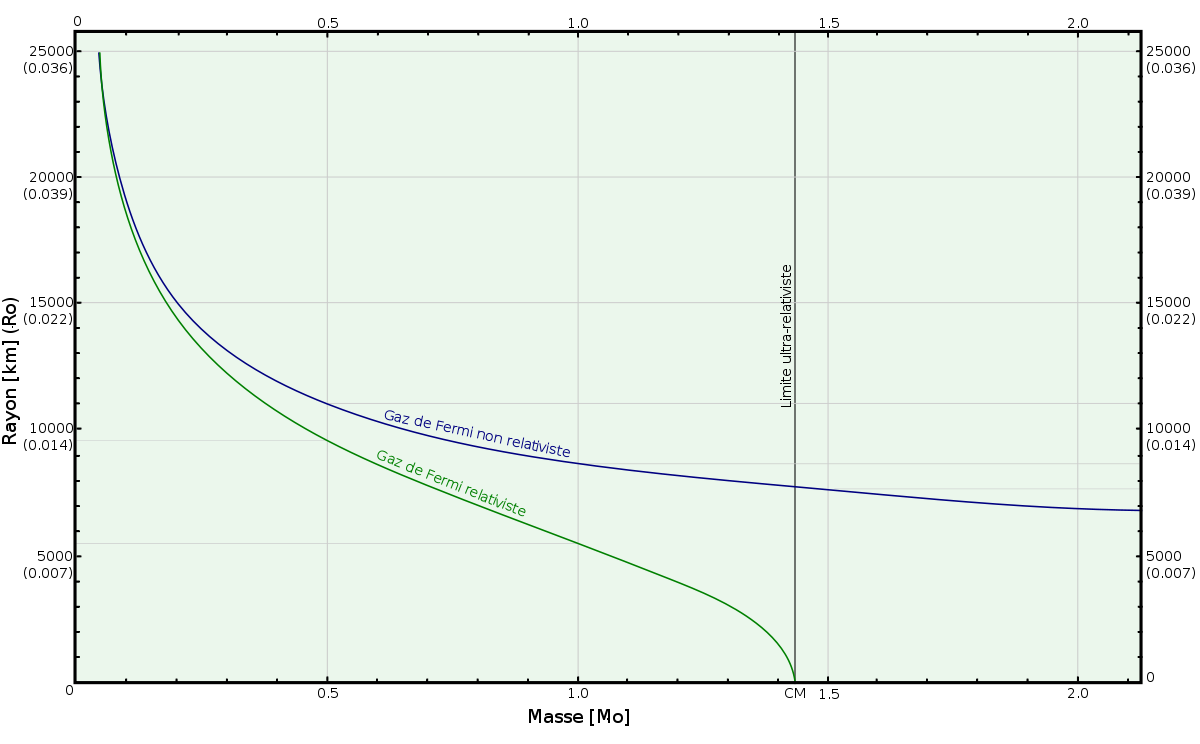
c'est-à-dire que le rayon d'une naine blanche est inversement proportionnel à la racine cubique de sa masse. Puisque cette analyse utilise la formule non relativiste p²/2m pour l'énergie cinétique, elle est non relativiste. Si nous désirons analyser la situation où la vitesse de l'électron dans une naine blanche est proche de la vitesse de la lumière, c, nous devons remplacer p²/2m par l'approximation relativiste extrême p c pour l'énergie cinétique. Avec cette substitution, nous trouvons :

Si nous mettons ceci en équation avec la magnitude E_g, nous trouvons que R s'élimine et que la masse M est forcément :

Pour interpréter ce résulat, observons que si nous ajoutons de la masse à une naine blanche, son rayon diminue ; aussi, selon le principe d'incertitude, le moment et donc la vitesse de ses électrons s'accroissent. Lorsque la vitesse approche c, l'analyse relativiste extrême devient plus exacte, ce qui signfie que la mase M de la naine blanche doit approcher M_limite. En conséquence, aucune naine blanche ne peut être plus lourde que la masse limite M_limite.