Supersymétrie - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Naissance de la supersymétrie - Description

Introduction

Note : Pour profiter au mieux de cet article, le lecteur devrait avoir de bonnes notions sur le spin, la physique des particules et la symétrie en physique.

La supersymétrie (abrégé en SuSy) est une symétrie supposée de la physique des particules qui postule une relation profonde entre les particules de spin demi-entier (les fermions) qui constituent la matière et les particules de spin entier (les bosons) véhiculant les interactions. Dans le cadre de la SuSy, chaque fermion est associé à un « superpartenaire » de spin entier, alors que chaque boson est associé à un « super-partenaire » de spin demi-entier.

Naissance de la supersymétrie

Théorème No-Go de Coleman et Mandula

Le modèle standard de la physique des particules a été presque entièrement construit grâce aux concepts de symétrie et d'invariance.

L'histoire de la supersymétrie commence dans les années 1960. A cette époque, l'ensemble des symétries considérées appartenaient au groupe de Poincaré. Des physiciens curieux se sont naturellement posé la question de savoir si ce groupe pouvait être étendu. On s'intéressa notamment à l'extension de la symétrie $S U (3)$ de saveur (à ne pas confondre avec $S U (3)$ de couleur) à $S U (6)$ dans un cadre relativiste. Toutes les tentatives échouent, et un théorème no-go brise tous les espoirs.

Sidney Coleman et Jeffrey Mandula publient leur article en 1967. Ils démontrent que le groupe de Poincaré est le groupe de symétrie le plus général de la matrice S. Leur démonstration se fonde sur les hypothèses suivantes :

Pour une masse M donnée, il existe un nombre fini de types de particules de masse inférieure à M
Les amplitudes correspondant à des diffusions élastiques sont des fonctions analytiques des variables s (énergie du centre de masse) et de l'angle de diffusion.
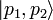
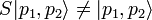
Soit $|p_1,p_2\rangle$ un état à deux particules, $S|p_1,p_2\rangle \neq |p_1,p_2 \rangle$ sauf pour certaines valeurs isolées de s.
Les opérateurs de symétrie sont définis à travers leurs relations de commutation, ceux-ci forment une algèbre de Lie.

C'est le dernier point qui va permettre de contourner le no-go théorème afin d'introduire la supersymétrie, dans une super-algèbre de Lie.

Intérêt phénoménologique

L'un des grands intérêts de la supersymétrie, au niveau phénoménologique, vient de la stabilisation du boson de Higgs, et donc la hiérarchie des masses des particules élémentaires.

Les corrections radiatives dans le modèle standard sont considérées comme bien maitrisées pour les fermions et pour les bosons de jauge. Pour les fermions, les corrections sont logarithmiques et surtout proportionnelles à la masse de la particule, ce qui assure l'ordre de grandeur. Pour une particule de masse nulle, elles sont nulles, et on retombe sur un modèle avec une symétrie supplémentaire qui protège les fermions : la symétrie chirale. Pour les bosons de jauges, l'invariance de jauge assure le même genre de "protection" aux masses. On constate que pour les deux cas, une "symétrie" empêche les corrections d'atteindre des échelles trop importantes, puisqu'elles doivent être proportionnelles au "degré de brisure" de la symétrie.

Or il existe dans le modèle standard un autre type de particule, le boson de Higgs, qui est introduit afin d'expliquer pourquoi certains bosons acquièrent des masses et brisent ainsi la symétrie de l'interaction.

Il s'avère que la masse du Higgs est dangereusement divergente, puisqu'elle dépend quadratiquement de l'échelle d'énergie.

Mais le vrai souci vient du fait que le modèle standard n'est considéré par la majorité des physiciens comme un modèle à basse énergie qui doit, à partir d'une certaine échelle donner la main à un autre modèle qui inclut plus de phénomènes. Ceci implique que les divergences ne peuvent pas être simplement absorbées dans la procédure de renormalisation, puisqu'on se retrouve très rapidement dans des régimes énergétiques qui ne sont pas censés être décrits par le modèle standard (à cause de la dépendance en carré), alors qu'on se place justement à des énergies correspondant au modèle standard.

La supersymétrie est une des solutions proposées pour atténuer l'effet de ces corrections, en introduisant une symétrie entre bosons et fermions. Cette symétrie assure en effet que pour une particule de spin $j$ , on peut avoir une particule de spin $j \pm \frac 12$ (suivant le cas), mais surtout que ces particules qui sont liées ainsi auront des contributions opposées, qui finissent donc par s'annuler.